Ý nghĩa động học của nhiệt độ
“Temperature” là chương trình viết ra với mục đích miêu tả quá trình cân bằng nhiệt giữa các thành phần vĩ mô, qua đó làm sáng tỏ những vấn đề sau:
– Sự cân bằng vĩ mô của vận động.
– Ý nghĩa động học của nhiệt độ.
– Bản chất của áp suất chất khí.
– Định luật Avogadro.
– Sự biến đổi nội năng của chất khí.
Sử dụng chương trình
Mô hình của chúng ta gồm một bình chứa hai khí riêng biệt, ngăn cách nhau bằng một vách ngăn trượt không ma sát. Ta có thể chọn khối lượng và kích thước cho mỗi loại phân tử, chọn số lượng hạt cho mỗi bên. Và cuối cùng, chọn giá trị ban đầu của nhiệt độ. Vách ngăn cũng có khối lượng mặc định bởi chương trình, nó nặng hơn mỗi hạt từ 2,5 đến 25 lần tuỳ chỉnh.
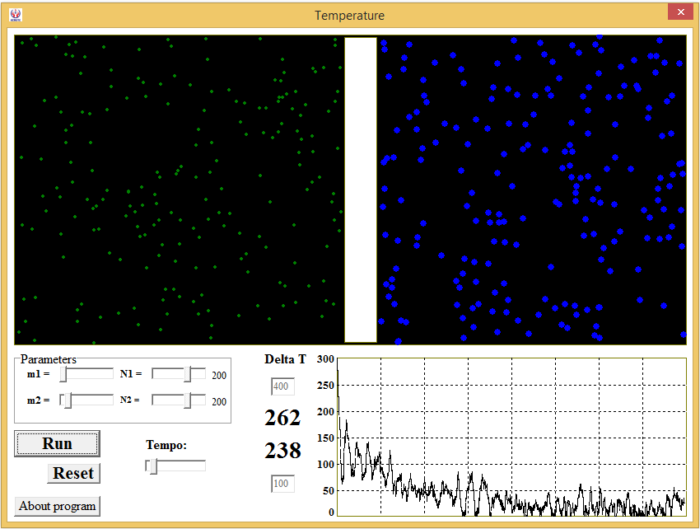
Khi khởi động quá trình, các phân tử sẽ va chạm lẫn nhau, va chạm vào thành bình và va chạm với vách ngăn. Chính nhờ vách ngăn mà hai loại khí không bị trộn lẫn vào với nhau. Tuy thế, vách ngăn chính là vật trung gian để tạo ra cân bằng nhiệt. Mục đích của chúng ta là quan sát quá trình cân bằng nhiệt thông qua va chạm với vách ngăn này.
Đồ thị màu đỏ bên dưới thể hiện mức chênh lệch nhiệt độ. Quá trình cân bằng nhiệt sẽ từ từ diễn ra, có thể khá chậm, và tạo thành đồ thị tiệm cận mức 0.
Thanh Tempo (nhịp độ) điều chỉnh tốc độ của quá trình, về bản chất là thay đổi sai số. Nếu muốn nhịp độ tăng nhanh (khỏi phải đợi lâu), cần chấp nhận sai số lớn hơn. Trong một số trường hợp cực đoan, như nhiệt độ quá lớn, nhịp độ quá nhanh, số hạt quá nhiều hoặc quá chênh lệch… chương trình có thể chạy không đúng vì vượt giới hạn máy tính.
Mô hình và thuật toán
Ở đây có hai loại va chạm được mô hình hóa, khiến cho quá trình diễn ra sinh động như thật:
Va chạm giữa các hạt với nhau
Các hạt phân tử mô hình hóa theo mẫu hình cầu nhẵn tuyệt đối. Chúng va chạm xuyên tâm với nhau theo các định luật bảo toàn động lượng và bảo toàn cơ năng. Chương trình sẽ kiểm tra khoảng cách giữa các hạt, nếu khoảng cách giữa các tâm nhỏ hơn 2 lần bán kính, sự va chạm sẽ diễn ra. Vì khối lượng các hạt cùng loại như nhau, nên thực ra chúng chỉ trao đổi thành phần vận tốc xuyên tâm.
Ba bậc tự do của hạt mô hình sẽ mô hình hóa tốt cho trường hợp khí trơ (He, Ne, Argon…), khi phân tử cũng là nguyên tử.
Sự va chạm lẫn nhau cũng giúp các phân tử trao đổi năng lượng và hình thành quy luật vĩ mô về phân bố vận tốc, hay Phân bố Maxwell.
Va chạm giữa hạt với vách ngăn
Điểm đặc biệt của vách ngăn là chỉ có một bậc tự do theo phương ngang. Do đó va chạm thực ra chỉ diễn ra theo thành phần \(x\). Khối lượng của vách ngăn lớn hơn khối lượng hạt nhiều lần, nên vách ngăn chỉ bị gia tốc nhẹ. Vì đề cao tính miêu tả nên khối lượng vách ngăn không đặt quá lớn, để cho quá trình diễn ra linh động, nhanh chóng hơn.
Khi vách ngăn bị gia tốc tạo chuyển động, bản thân nó cũng sẽ ảnh hưởng đến khối khí bên kia khi va chạm với chúng, chia sẻ năng lượng với chúng. Thành ra cuối cùng, năng lượng chuyển động giữa hai khối khí dần dần san sẻ cho nhau và đi đến cân bằng nhiệt độ.
Cách tính nhiệt độ
Nhiệt độ ở đây sử dụng khái niệm từ vật lý thống kê, dành cho khí lý tưởng, tỉ lệ thuận với động năng trung bình của chuyển động tịnh tiến. Với các khí trơ (He, Ne…), tỉ lệ này diễn đạt qua công thức:
\[E = \frac{3}{2}kT,\]
trong đó \(k\) – hệ số tỉ lệ, được gọi là hằng số Boltzmann.
Chương trình sẽ tính tổng động năng của các hạt, sau đó chia đều cho số hạt thu được động năng trung bình, sau cùng liên hệ với công thức trên để suy ra nhiệt độ.
Những kết quả cơ bản
Cân bằng động năng
Theo phương pháp tính nhiệt độ nói trên, nhiệt độ chính là động năng trung bình của chuyển động. Phép cân bằng nhiệt từ những va chạm sơ đẳng, thuần túy cơ học cho thấy rằng, hệ va chạm cuối cùng rồi sẽ đi đến một trạng thái bền vững, trong đó động năng trung bình của mỗi hạt ở cả hai bên vách ngăn đều bằng nhau, mặc cho kích thước, khối lượng, bản chất của hạt ở hai bên là khác nhau! Chính động năng trung bình chứ không phải động lượng hay đại lượng nào khác làm thước đo cho phép cân bằng tổng thể.
Chúng ta thấy được sự cân bằng vĩ mô thông qua sự cân bằng năng lượng chuyển động. Do đó người ta đã phát biểu rằng: nhiệt độ là thước đo cho mức độ chuyển động vi mô của hệ. Chủ đề này ta sẽ nói kĩ hơn ở phần lý thuyết.
Cân bằng áp suất
Cân bằng cơ học là điều bắt buộc cho mọi hệ cân bằng. Cho dù chưa đạt đến cân bằng nhiệt đi nữa, cân bằng về lực vẫn phải được thiết lập, dù chưa bền vững. Trạng thái bền vững cuối cùng cần đạt nhiều loại cần bằng cùng một lúc: cân bằng cơ học, cân bằng nhiệt, cân bằng thế nhiệt động (cân bằng pha)…
Vách ngăn bị va đập từ cả hai phía, nó rung động liên hồi. Với hệ thực, rung động này trở nên dày đặc và liên tục, tạo nên sự bình ổn về lực, gọi là áp suất. Ở trạng thái cân bằng sau cùng, vách ngăn đã nằm tại vị trí nào đó khá ổn định, cho dù có ít nhiều biến động quanh vị trí cân bằng, vật lý gọi là “thăng giáng”. Từ đây người quan sát dễ dàng hiểu được nguyên nhân tạo thành áp suất của chất khí.
Đặc biệt, khi số lượng hạt không bằng nhau, giả sử rằng bên trái có nhiều hạt gấp đôi bên phải, vách ngăn sẽ đạt đến vị trí cân bằng bền vững, sao cho thể tích khối khí bên trái lớn gấp đôi thể tích của khối khí bên phải, hay nói cách khác, mật độ khí hai bên sẽ bằng nhau. Đó cũng chính là nội dung của định luật Avogadro, theo đó hai khối khí bất kì có cùng một áp suất và cùng một thể tích phải chứa cùng một số lượng hạt như nhau.
Định luật này có thể miêu tả qua phương trình trạng thái Claperon – Mendeleev dành cho khí lý tưởng, viết theo dạng vi mô:
\[p = nkT,\]
trong đó \(n\) là mật độ khí. Áp suất tỉ lệ thuận với mật độ hạt, tức cũng tỉ lệ với tần suất va đập của hạt lên thành bình.
Lý thuyết động học phân tử
Về sự cân bằng nhiệt
Lý thuyết động học phân tử là một trong những học thuyết quan trọng bậc nhất của khoa học, phát triển một cách có hệ thống và mang phép định lượng từ nửa sau thế kỉ 19 đến đầu thế kỉ 20. Việc vật chất được cấu thành từ phân tử và nguyên tử vốn không có gì mới từ thế kỉ 16-17. Việc chấp nhận thuyết cấu tạo chất từ phân tử và nguyên tử đã giải thích nhiều hiện tượng, trong đó có sự phối hợp giữa các chất theo những tỉ lệ đơn giản, giúp hóa học phát triển trong thời gian dài sau đó.
Tuy vậy một lý thuyết chặt chẽ, mang tính định lượng có thể kiểm định thực tế chỉ có thể được hình thành vào nửa sau thế kỉ 19, khi người ta bắt đầu áp dụng cơ học Newton vào mô hình chuyển động phân tử. Cụ thể hơn, đó là các định luật bảo toàn xung lượng và cơ năng của chuyển động. Điều này hình thành nên bộ môn vật lý thống kê, giải thích các hiện tượng nhiệt thông qua quy luật cơ học.
Các chứng minh chặt chẽ đã đi đến kết quả rằng, động năng trung bình của chuyển động tịnh tiến của phân tử, nguyên tử, tương ứng với mỗi bậc tự do, không phân biệt khối lượng, kích thước, bản chất, không phân biệt rắn, lỏng, khí… đều bằng nhau ở trạng thái cân bằng. Như vậy, các phân tử của hạt phấn hoa trong chuyển động Brown cũng có động năng trung bình bằng với động năng trung bình của phân tử nước. Đặc biệt hơn, động năng tịnh tiến trung bình của chính hạt phấn hoa cũng bằng động năng trung bình của phân tử nước và của các phân tử cấu tạo nên chính nó!
Ở đây cần phân biệt động năng tịnh tiến của hạt phấn và tổng động năng các phân tử phấn hoa. Vì phân tử dao động hỗn loạn, cho nên động năng của khối tâm hạt phấn không bằng tổng động năng phân tử. Nó bão hòa, nhưng thăng giáng, và tạo ra dao động rất nhỏ. Thú vị là dao động này có động năng trung bình bằng động năng trung bình của phân tử cấu tạo nên chính hạt phấn. Còn tổng động năng các phân tử của hạt phấn thì góp phần tạo nên nội năng của hạt.
Thước đo nhiệt độ theo cơ học, cầu nối giữa thế giới vĩ mô và vi mô.
Hằng số Boltzmann.
Theo quan điểm từ Nhiệt động lực học, đại lượng chung nhất đặc trưng cho trạng thái cân bằng chính là nhiệt độ. Nhiệt động lực học là bộ môn khoa học chính xác nhất về các hiện tượng nhiệt, đưa ra khái niệm nhiệt độ rất tổng quát. Nếu so sánh với kết quả chứng minh từ lý thuyết động học phân tử, theo đó động năng chuyển động tịnh tiến là đại lượng đồng nhất, chung nhất của hệ khi cân bằng, thì ta có thể đưa ra kết luận: có thể dùng động năng chuyển động tịnh tiến làm thước đo nhiệt độ.
Ta có tỉ lệ:
\[E\sim T.\]
Vì năng lượng và nhiệt độ đã được hình thành trước đó, với thang đo và đơn vị khác nhau, do đó cần phải lấy một hệ số tỉ lệ làm cầu nối. Các nhà khoa học quy ước:
\[E=\frac{1}{2}kT\]
ứng với một bậc tự do. \(k\) – hằng số Boltzmann, là một trong những hằng số quan trọng nhất trong vật lý, cho phép liên hệ nhiệt độ với vận động. Với hằng số Boltzmann, thuật ngữ “chuyển động nhiệt” đã không còn là câu nói suông nữa.
Xác định giá trị các hằng số Boltzmann và Avogadro
Hai hằng số này lại có liên hệ với nhau qua hệ thức:
\[R=kN_A.\]
Trong đó \(R\) là hằng số khí lý tưởng, có thể dễ dàng xác định qua thực nghiệm với bình khí, nhiệt kế và áp kế chữ \(U\):
\[PV=RT.\]
Như vậy biết được hằng số Boltzmann sẽ biết được hằng số Avogadro và ngược lại. Tuy nhiên xác định số Avogadro là không tưởng. Số Avogadro chính là số hạt vi mô chứa trong 12g đồng vị Carbon-12. Trong hóa học, số Avogadro và mol là cầu nối giữa vi mô với vĩ mô. Với các phản ứng, giá trị của số Avogadro không quá quan trọng (miễn rằng đủ lớn), bởi vì khoa học của phản ứng là khoa học của tỉ lệ, của số mol, không phải của số phân tử. Nhưng với sự vận động thì lại khác, vì hằng số Boltzmann ảnh hưởng đến mức độ vận động của vi hạt. Việc xác định hằng số Boltzmann có thể thực hiện thông qua mức độ vận động của hạt.
Thực nghiệm cho thấy vận tốc chuyển động của phân tử cực kì lớn, lên đến hàng nghìn m/s ở điều kiện thông thường. Do vậy xác định động năng của phân tử rồi chia cho nhiệt độ \(T\) để lấy hằng số Boltzmann cũng không khả thi.
Nhưng tại phần lý thuyết 1, ta đã biết rằng, động năng trung bình của hạt phấn hoa cũng bằng với động năng trung bình phân tử. Đo chuyển động zic zak chậm rãi của hạt phấn có khối lượng lớn (hạt Brown), ta có thể xác định mức độ vận động của hạt Brown để suy ra hằng số Boltzmann và hằng số Avogadro.