Phân bố vi hạt theo năng lượng
“Statistical Distributions” – “Phân bố vi hạt theo năng lượng” là chương trình máy tính mô phỏng quá trình hình thành sự phân bố của hệ vi hạt tuân theo một trong ba quy luật sau:
– Phân bố Boltzmann, dành cho các hạt cổ điển.
– Phân bố Fermi–Dirac, dành cho các fermion, hay các hạt có spin lẻ như electron, proton, neutron…
– Phân bố Bose–Einstein, dành cho các boson, hay các hạt có spin nguyên như photon (hạt ánh sáng), phonon (hạt âm thanh)…
Với phân bố thống kê Boltzmann, chúng ta khá dễ hình dung bởi vì các hạt chỉ tuân theo quy luật va chạm cơ học thông thường. Một ví dụ rất điển hình chính là quy luật phân bố mật độ của bầu khí quyển Trái đất. Vì vậy, với phân bố Boltzmann, ta có thể liên tưởng đến sự phân bố mật độ không khí trong khí quyển.
Còn các loại phân bố Fermi và Bose chỉ dành cho các hạt chuyển động theo quy luật của vật lý lượng tử. Do đó việc diễn tả chúng qua hình ảnh hết sức khó khăn. Tuy vậy, chương trình giới thiệu lần này nhằm đạt đến mục đích diễn tả tất cả các loại phân bố thống kê theo năng lượng, không phân biệt cổ điển hay lượng tử, bằng những va chạm cơ học trực quan. Có thể nói rằng đây là sản phẩm độc đáo chưa trùng lặp trên thế giới.
Video minh hoạ
Mô hình và hoạt động của chương trình
Hình dung rằng chúng ta đang quan sát một bầu khí quyển cấu thành từ các phân tử Nitrogen, có độ dày 10 km. So với bán kính 6371 km của quả đất, độ dày rất mỏng này cho phép xem các hạt chuyển động trong trường lực đều, với gia tốc hướng xuống bằng \(9.8\mathrm{m/s^2}\).
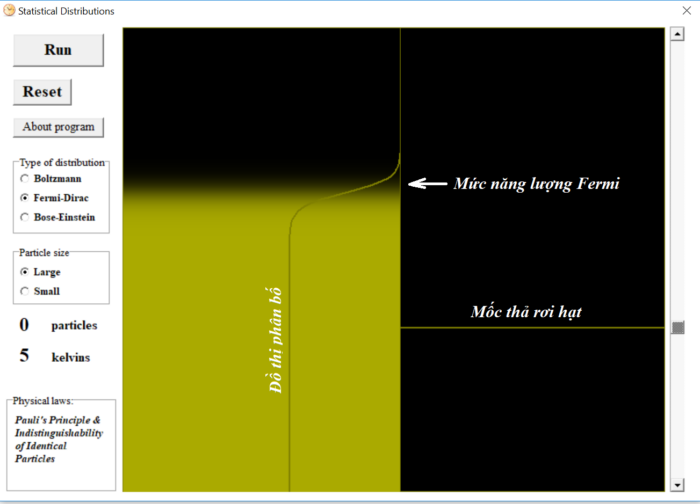
Cột không khí này lại được chia thành nhiều lớp, phân biệt nhau bởi thế năng. Bởi do thế năng phụ thuộc tuyến tính vào độ cao theo công thức:
\[E=mgh.\]
Ta nghiên cứu phân bố vi hạt theo năng lượng, nhưng sẽ quy về theo dõi sự phân bố mật độ theo độ cao, vì động năng trung bình – hay nhiệt độ không phân biệt theo vị trí. Mỗi lớp khí quyển như thế lại chứa \(G\) trạng thái có cùng một mức năng lượng.
Với thanh trượt thẳng đứng ngoài cùng bên phải, ta có thể thay đổi độ cao ban đầu \(h_0\) của vi hạt. Máy tính sẽ tính toán nhiệt độ mà hệ sẽ đạt được khi cân bằng, đồng thời biểu diễn mật độ phân bố theo lý thuyết.
Mật độ phân bố này đồng thời biểu diễn theo hai cách:
– Đồ thị của hàm phân bố.
– Gradient của màu sắc theo mật độ. Với cách này ta sẽ dễ hình dung hơn về “độ đậm đặc” của bầu khí quyển.
Sau khi chọn độ cao \(h_0\) ban đầu, ta đã có thể khởi động bằng nút “RUN”. Các hạt sẽ tuần tự nối đuôi nhau rơi tự do từ độ cao ban đầu đã chọn. Tổng số hạt khảo sát gồm \(N=200\) nếu đặt chế độ hạt lớn, \(N=400\) nếu đặt chế độ hạt nhỏ. Tuy có năng lượng ban đầu như nhau, nhưng qua nhiều lần va chạm các hạt sẽ bị phân bố về các trạng thái khác nhau từ thấp đến cao.
Đặc biệt, ta có thể thay đổi tức thời quy luật phân bố qua các nút lựa chọn. Bằng cách này chúng ta sẽ dễ hình dung hơn về nguyên nhân tạo ra các loại phân bố khác nhau. Khi thay đổi quy luật va chạm, tổng năng lượng của hệ không bị thay đổi.
Các định luật vật lý quan sát được
Phân bố Boltzmann
Các hạt va chạm tự do theo quy luật cơ học cổ điển như những quả bóng hình cầu. Ngoài va chạm với bề mặt đáy, thành hai bên, va chạm lẫn nhau, các hạt không bị ràng buộc thêm bởi điều gì khác.
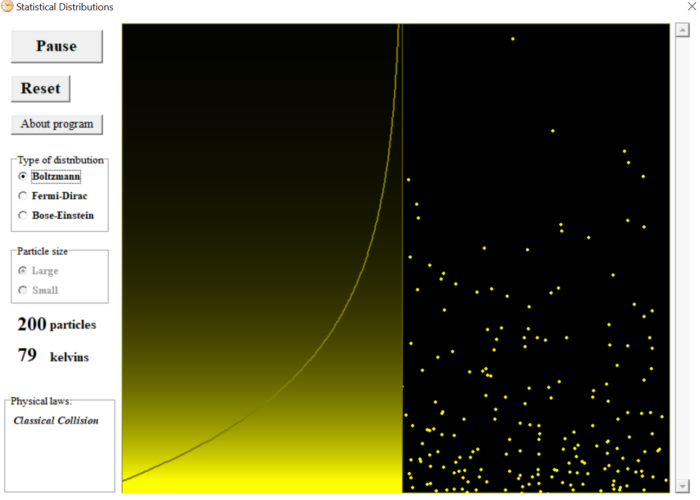
Phân bố Boltzmann biểu diễn sự phụ thuộc của mật độ vi hạt vào năng lượng:
\[n=n_0e^{-\frac{\varepsilon_p}{kT}}.\]
trong đó \(\varepsilon_p\) – thế năng của hạt trong trường ngoại lực, \(k\) – hằng số Boltzmann, \(T\) – nhiệt độ tuyệt đối. Sự phân bố mật độ khí quyển Trái đất là một trường hợp riêng của phân bố Boltzmann:
\[n=n_0e^{-\frac{mgh}{kT}}.\]
Áp suất khí lại tỉ lệ với mật độ phân tử khí: \(p=nkT\). Từ đây ta có công thức của áp suất khí quyển Trái đất theo độ cao:
\[p=p_0e^{-\frac{mgh}{kT}}.\]
Quan sát phân bố Boltzmann qua chương trình “Statistical Distributions” là chúng ta đang quan sát bầu khí quyển thực tế của Trái đất.

Phân bố Fermi-Dirac
Ngoài phép va chạm thông thường như bên phân bố Boltzmann, các fermion bị ràng buộc thêm bởi hai quy luật khắc nghiệt:
– Quy luật 1: Nguyên lý cấm Pauli.
– Quy luật 2: Nguyên lý không phân biệt các hạt đồng nhất.
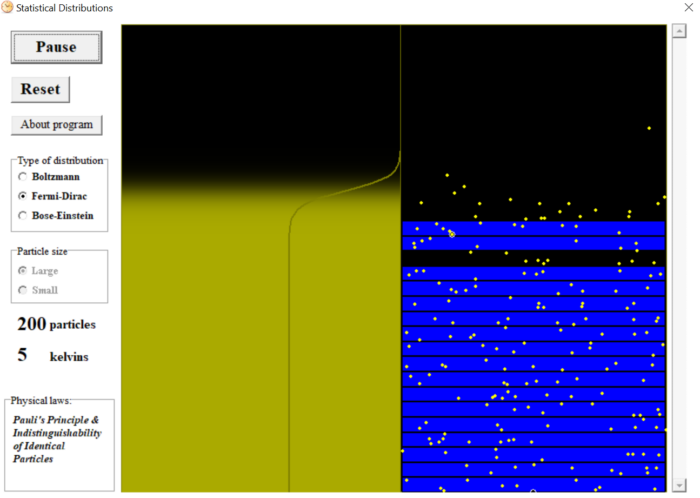
Theo nguyên lý Pauli, ứng với mỗi trạng thái chỉ cho phép tồn tại tối đa đúng 1 vi hạt. Như vậy trong mô hình của chúng ta, mỗi lớp “khí quyển” có đúng \(G\) trạng thái. Theo mô hình hạt nhỏ \(G=20\), còn mô hình hạt lớn \(G=10\). Nói cách khác, mỗi lớp như thế không thể chứa quá \(G\) hạt. Khi có một lớp nào đó bị đầy, lớp đó được tô nền màu xanh, và không cho phép có thêm một hạt từ nơi khác xâm phạm vào. Do đó khi đặt chế độ Fermi-Dirac, ta sẽ quan sát thấy rất nhiều va chạm diễn ra trên các lớp phân cách của các vùng màu xanh hay vùng cấm.
Theo nguyên lý không phân biệt các hạt đồng nhất, các hạt được xem là tuyệt đối giống nhau. Tuy nhiên nếu hiểu như vậy cũng chưa đủ. Sự không phân biệt các hạt phải được hiểu theo ý nghĩa sau đây: Việc hoán đổi trạng thái của hai vi hạt bất kì cũng không làm thay đổi trạng thái chung của hệ. Từ ý nghĩa nói trên, mô hình của chúng ta đã gài thêm môt phép hoán đổi ngẫu nhiên giữa hai hạt bất kì, tức hai hạt bất ngờ thay đổi vị trí cho nhau. Đó là lý do tại sao ta thường xuyên quan sát thấy các chớp sáng trên màn hình: các hạt vừa bị hoán đổi trạng thái.
Hàm phân bố mật độ vi hạt theo Fermi-Dirac, biểu diễn bên khung hình bên trái của chương trình, có dạng:
\[n_i=\frac{G_i}{e^{\frac{\varepsilon_i-\mu}{kT}}+1},\]
trong đó \(n_i\) – mật độ vi hạt ở lớp thứ \(i\), \(\mu\) – thế hoá học. Thế hoá học này có giá trị được xác định qua điều kiện chuẩn hoá:
\[\sum\limits_{i=1}^\infty{\frac{G_i}{e^{\frac{\varepsilon_i-\mu}{kT}}+1}}=N,\]
Với \(N\) là tổng số hạt khảo sát.
Lưu ý: Không phải độ cao ban đầu nào của hạt cũng tạo ra được phân bố Fermi. Nếu độ cao ban đầu quá thấp, phân bố sẽ không đạt được, còn theo lý thuyết nhiệt độ tuyệt đối sẽ trở thành số âm. Khi ấy chương trình vẫn chạy nhưng không mang ý nghĩa vật lý thực tế.
Phân bố Bose-Einstein
Các boson lại không tuân theo nguyên lý cấm Pauli, nhưng cũng là các hạt lượng tử, nên chúng vẫn phải tuân theo nguyên lý không phân biệt các hạt đồng nhất. Nói các khác, việc mô hình hoá chuyển động của các boson cũng tương tự như phân bố Boltzmann, chỉ cần thêm vào phép hoán đổi trạng thái như đã áp dung với phân bố Fermi-Dirac.
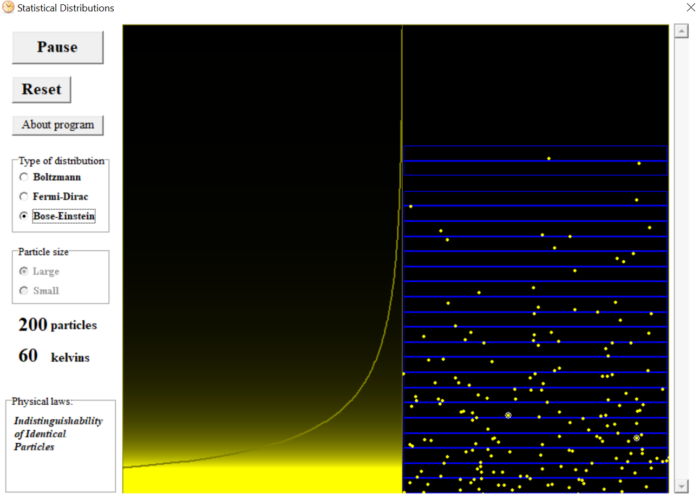
Hàm phân bố mật độ vi hạt theo Bose-Einstein, biểu diễn bên khung hình bên trái của chương trình, có dạng:
\[n_i=\frac{G_i}{e^{\frac{\varepsilon_i-\mu}{kT}}-1},\]
trong đó \(n_i\) – mật độ vi hạt ở lớp thứ \(i\), \(\mu\) – thế hoá học. Thế hoá học này có giá trị được xác định qua điều kiện chuẩn hoá:
\[\sum\limits_{i=1}^\infty{\frac{G_i}{e^{\frac{\varepsilon_i-\mu}{kT}}-1}}=N,\]
Với \(N\) là tổng số hạt khảo sát.