Phương trình chuyển động và phương trình quỹ đạo là hai khái niệm căn bản trong việc miêu tả chuyển động của một chất điểm. Bài viết này trong chuỗi “Mô phỏng Matlab” với ngôn ngữ Matlab giúp chúng ta hình chung chính xác và dễ dàng.
Xét một chuyển động ném ngang với vận tốc đầu \(v_0=10\) m/s, ném từ độ cao \(h_0=50\) m. Quy luật biến đổi vị trí của vật theo thời gian được diễn tả qua hệ phương trình:
\[\begin{aligned}x&=v_0t,\\y&=h_0-\dfrac{1}{2}gt^2.\end{aligned}\tag{1}\]
Trong đó \(g\) là gia tốc rơi tự do. Biểu thức toán học diễn tả sự biến đổi của vị trí theo thời gian được gọi là phương trình chuyển động.
Trong Matlab, phương trình chuyển động (1) được miêu tả qua chương trình sau:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | function ptcd_ptqd clc clear all close all %% INPUT DATA v0 = 10; h0 = 50; g = 9.81; t = linspace(0,3.5,500); %% CALCULATION x = v0*t; y = h0-0.5*g*t.^2; %% FIGURE figure('name','Phuong trinh chuyen dong','color','white','numbertitle','off'); plot(t,x,'linewidth',2); hold on plot(t,y,'linewidth',2); legend('x','y'); xlabel('Thoi gian'); ylabel('Toa do'); end |
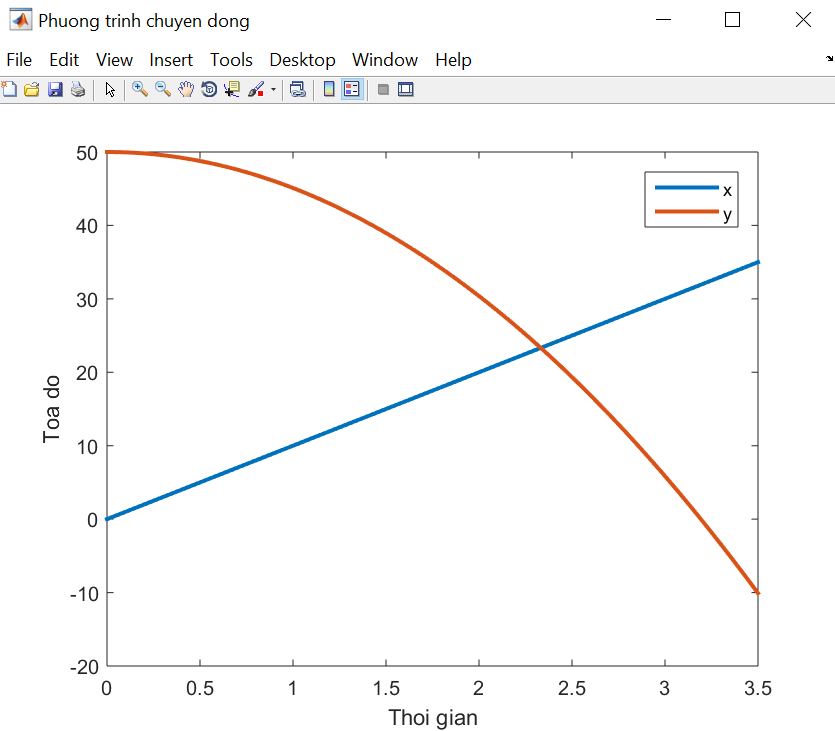
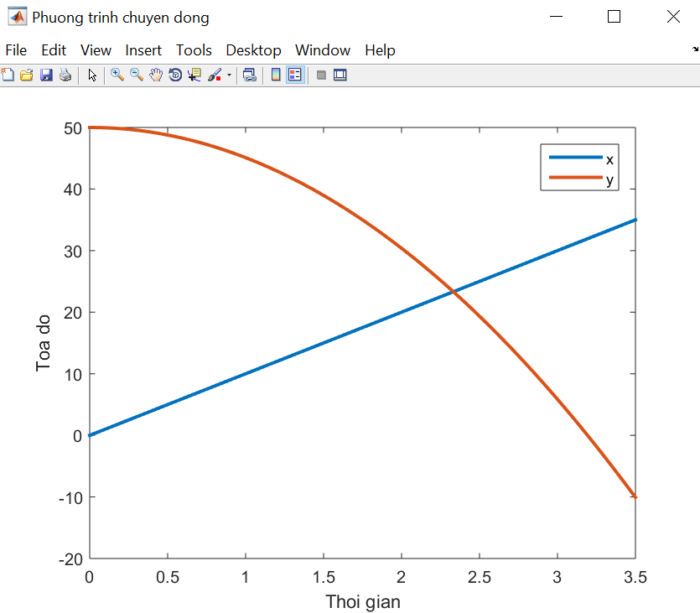
Các lệnh trong INPUT DATA khai báo tham số chuyển động, đồng thời tạo mảng thời gian cần khảo sát, gồm 500 thời điểm từ 0 đến 3.5 giây. Các lệnh CALCULATION tạo các mảng đối số \(x\) và \(y\) theo hệ phương trình (1). Các lệnh trong FIGURE giúp vẽ đồ thị hàm số \(x(t)\) và \(y(t)\).
Khi khởi động chương trình, kết quả cho ra như hình dưới:
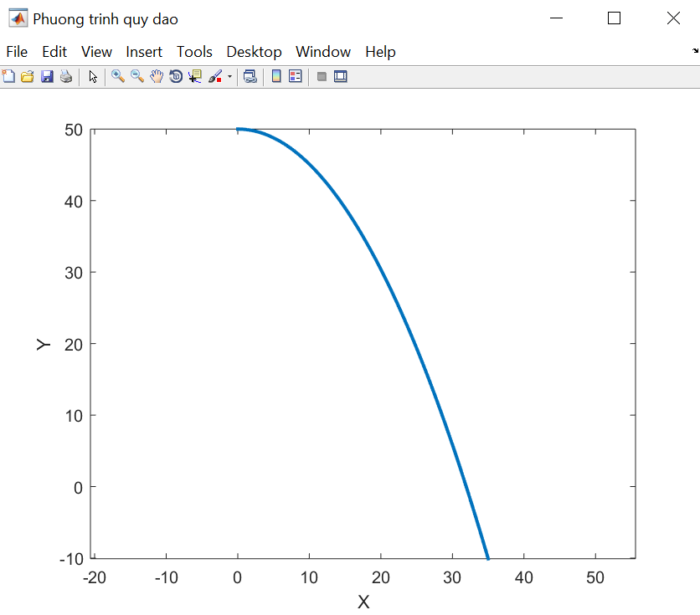
Từ phương trình chuyển động (1), ta có thể suy ra phương trình quỹ đạo của vật. Phương trình quỹ đạo là biểu thức toán học miêu tả hình dạng của quỹ đạo. Trong những trường hợp đơn giản, phương trình quỹ đạo \(y(x)\) có thể thu được qua phép khử biến số thời gian. Trong trường hợp tổng quát, khi phép khử thời gian trở nên khó khăn, phương trình quỹ đạo vẫn nhận được dễ dàng nhờ phương pháp số. Quy tắc rất đơn giản: kẹp hai mảng \(x\) và \(y\) vào nhau, \(x\) đóng vai trò như biến số độc lập, còn \(y\) trở thành biến số phụ thuộc \(x\). Chương trình tổng thể sau đây cho phép dựng cả phương trình quỹ đạo:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | function ptcd_ptqd clc clear all close all %% INPUT DATA v0 = 10; h0 = 50; g = 9.81; t = linspace(0,3.5,500); %% CALCULATION x = v0*t; y = h0-0.5*g*t.^2; %% FIGURE figure('name','Phuong trinh chuyen dong','color','white','numbertitle','off'); plot(t,x,'linewidth',2); hold on plot(t,y,'linewidth',2); legend('x','y'); xlabel('Thoi gian'); ylabel('Toa do'); figure('name','Phuong trinh quy dao','color','white','numbertitle','off'); plot(x,y,'linewidth',2); axis equal xlabel('X'); ylabel('Y'); end |
Lệnh “axis equal” có tác dụng chuẩn hoá các trục toạ độ về cùng một tỉ lệ. Kết quả tính toán quỹ đạo chỉ ra ở hình dưới. Có thể thấy rằng, quỹ đạo của vật ném ngang là một parabol úp xuống có đỉnh tại vị trí ném. Tầm xa của vật đạt được khoảng 30 m. Tất cả những điều này có thể kiểm chứng lại bằng phép tính giải tích thông thường.