Trạng thái dừng nguyên tử
“Trạng thái dừng nguyên tử” là chương trình mô phỏng nguyên lý tạo thành các trạng thái dừng của vi hạt trong hố thế cũng như electron trong nguyên tử. Xem chương trình này, chúng ta sẽ hiểu tại sao các hạt trong liên kết chỉ có các trạng thái rời rạc với mức năng lượng xác định. Đây là chương trình dành cho giáo dục, phục vụ sinh viên năm 2, năm 3 và những bạn quan tâm.
Với giao diện đơn giản cho dễ sử dụng, chương trình sử dụng đến một loạt các phép toán tinh vi về số phức, chuyển pha, chuyển hệ toạ độ… nhằm trang bị cho sóng lan truyền có khả năng phản xạ trên bất cứ vật cản nào nó gặp phải.
Video minh hoạ
Nguyên lý hoạt động của chương trình
Theo Louis de Broglie, mỗi hạt chuyển động tự do, tức chuyển động thẳng đều, tương đương với một sóng hình sin có dạng: \(\psi(x,t)=Ae^{-i(kx-\omega t)}\), trong đó \(k=2\pi/\lambda\), với \(\lambda\) là bước sóng. Ông cho rằng bước sóng này liên hệ với xung lượng của hạt theo hệ thức:
\[\lambda=\frac{h}{p},\]
trong đó \(h\) là hằng số Planck, \(p\) là xung lượng liên hệ với động năng \(T\) theo hệ thức:
\[p^2=(mv)^2=\frac{2T}{m}.\]
Mặt khác tổng động năng và thế năng là năng lượng toàn phần không đổi:
\[T+U= E.\]
Như vậy khi hạt chuyển động trong trường thế năng biến đổi, động năng cũng biến đổi, dẫn đến xung lượng cũng biến đổi. Cho nên bước sóng của hạt cũng biến đổi trong không gian:
\[\lambda=h\sqrt\frac{m}{2(E-U)}.\]
Có được nguyên tắc đó, ta có thể tính được sự lan truyền của sóng de Broglie qua một barrier (rào cản), một phần sẽ đi qua, còn một phần phản xạ ngược lại.
Mô phỏng sự hình thành trạng thái dừng
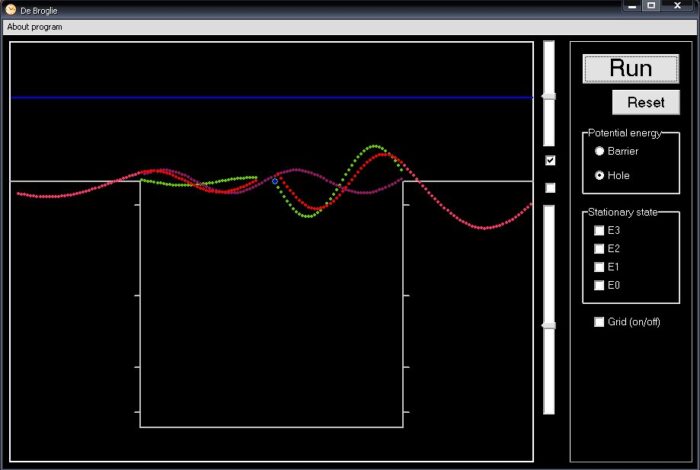
Trên hình 1, năng lượng của hạt đủ lớn để sóng có thể truyền qua, nhưng vẫn bị phản xạ lại một phần.
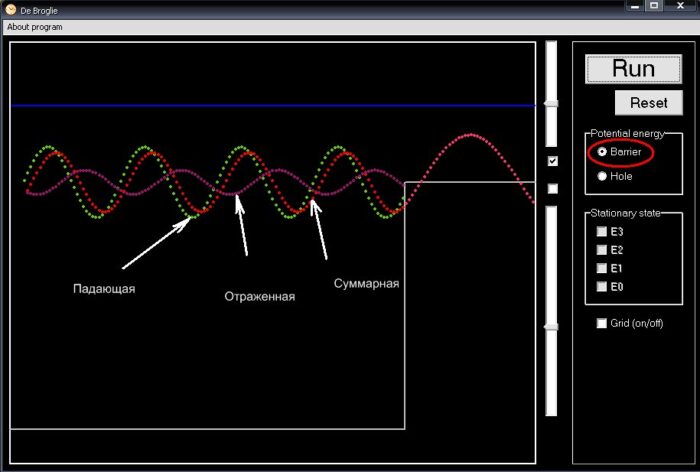
Trường hợp diễn tả trên hình 2, năng lượng của hạt thấp hơn giá trị cần có để vượt qua được bức tường. Sóng de Broglie không thể truyền qua được và bị dội ngược toàn phần theo hướng ngược lại. Tuy thế vẫn có một phần nhỏ sóng-hạt bị thấm qua bên kia vách. Lưu ý rằng lúc này đã hình thành sóng dừng. Phần hạt bị thấm qua vách cũng là sóng dừng, không bị sự lan truyền làm mất mát.
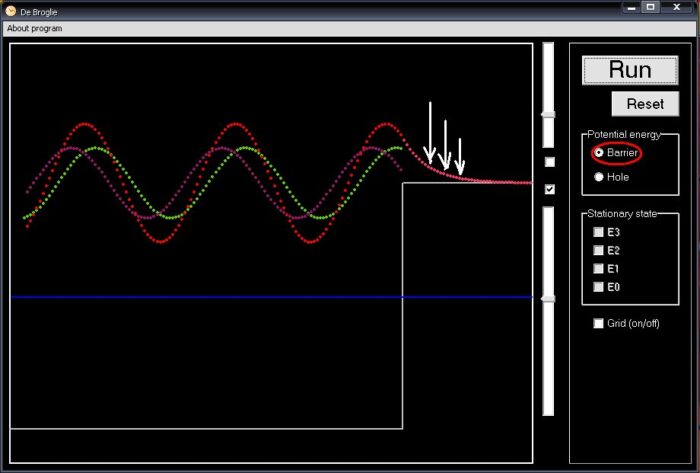
Phát triển ý tưởng theo hướng đó, ta xây dựng hố thế tạo bởi 2 barrier đối nghịch nhau như hình 3. Mặc dù mô hình này đơn giản nhưng nó phản ánh nét tương tự của một hạt electron gắn kết trong nguyên tử.
Khi hạt có năng lượng thấp hơn miệng hố, nó sẽ lần lượt bị phản xạ toàn phần từ barrier này sang barrier kia. Mỗi lần phản xạ như vậy sẽ tạo ra sóng dừng. Nhưng thường sóng dừng do phản xạ bên trái không trùng với sóng dừng do phản xạ bên phải. Do đó trạng thái sóng hết sức hỗn loạn, không ổn định. Nó tương ứng với năng lượng ngẫu nhiên nào đó. Phần khoanh tròn trên hình 3 thể hiện nét đứt gãy không hoà hợp của hai sóng phản xạ.
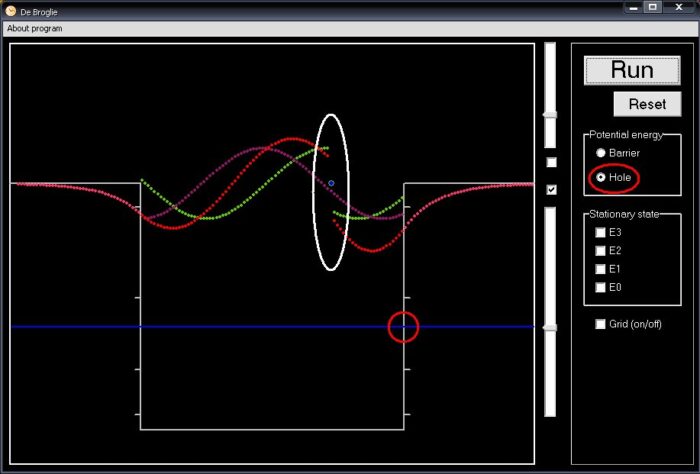
Nhưng nếu hạt có một năng lượng xác định nào đó, sao cho bước sóng của nó có độ dài thích hợp, các lần phản xạ qua về giữa hai bức tường sẽ cho ra bức tranh giao thoa tổng thể hài hoà. Khi đó sóng đã tuyệt đối “dừng”. Ta gọi đây là trạng thái dừng của hạt. Nó gắn liền với sóng dừng và một mức năng lượng xác định (hình 4).
Sóng này vẫn vận động biến đổi theo thời gian, nhưng theo quy luật dao động điều hoà. Nó đứng yên tại chỗ chứ không chạy. Phương trình của sóng này có dạng:
\[\psi(x,t)=\Psi(x)e^{i\omega t},\]
trong đó \(\Psi(x)\) là hàm số biên độ của dao động. Hàm số này là nghiệm của phương trình dừng Schrodinger.
Electron trong nguyên tử cũng chuyển động trong một hố thế hình thành bởi trường Coulomb của hạt nhân. Chỉ với những mức năng lượng xác định nào đó, sóng electron mới có chiều dài thích hợp với kích thước của hố thế hạt nhân.
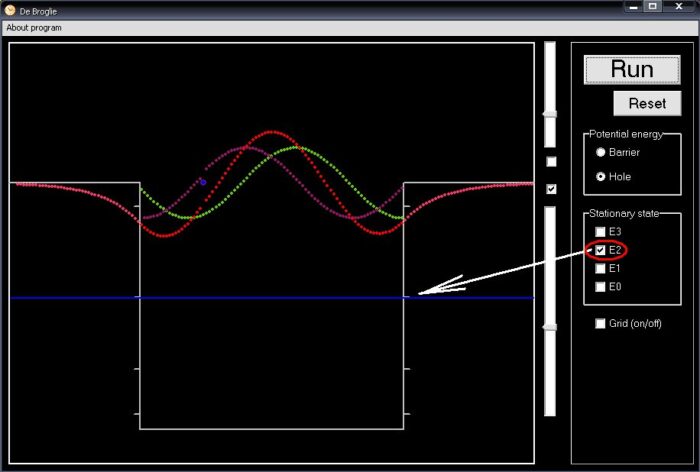
Chương trình này được thiết kế nhằm giúp ta nhìn thấy sự thay đổi liên lục và liên tục sự biến đổi các trạng thái của hạt, giữa các trạng thái dừng và trạng thái hốn loạn và giữa các trạng thái dừng với nhau. Trên hình 5 chỉ ra các mức năng lượng có khả năng tạo nên trạng thái dừng cho vi hạt. Ta thấy rằng, ở trạng thái tương ứng với mức năng lượng toàn phần thấp nhất, năng lượng ấy không phải bằng không. Điều này khác với hạt trong hố thế cổ điển, khi mức năng lượng thấp nhất phải nằm ngang đáy hố.
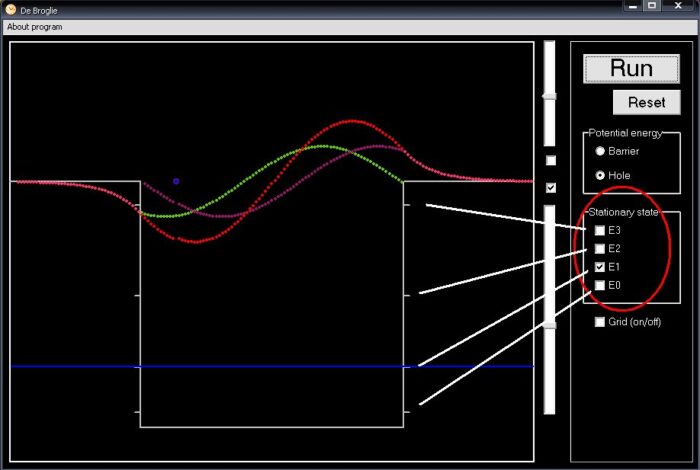
Nếu hạt có năng lượng cao hơn miệng hố, nó sẽ thoát ra ngoài (hình 6). Nhưng khác với kiểu hạt cổ điển vốn sẽ bay toàn bộ về một hướng nào đó, hạt theo quan điểm cơ học lượng tử lại giống như một đám mây mù, nó bị loang ra hai bên do khi va chạm với các barrier, chỉ một phần sóng chạy ra ngoài, phần còn lại phản xạ. Tương tự như thế, phần phản xạ ấy lại tràn qua phía bờ bên kia làm mất mát thêm phần nữa, một tỉ lệ trong số đó lại phản xạ quay trở lại hố. Cứ thế và cứ thế, “đám mây” hạt sẽ dần tản mát đi và biến mất ra xung quanh.