Xác định điện tích riêng electron bằng phương pháp magnetron
Trong bài thí nghiệm này ta xác định điện tích riêng của electron bằng phương pháp magnetron, khảo sát chuyển động của electron trong từ trường. Với sự trợ giúp của phần mềm mô phỏng, sinh viên có thể hình dung dễ dàng quỹ đạo của các hạt và nguyên lý hoạt động của dụng cụ thí nghiệm.
Chương trình mô phỏng thực hiện bởi sinh viên
ngành Công nghệ thông tin
Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh
Nguyễn Văn Rum
Hồ Anh Tú
Trần Ngọc Trọng
Lưu ý: chương trình chạy trên nền java
Nguyên lý phép đo
Điện tích riêng
Trong lịch sử phát triển của vật lý học, điện tích được định nghĩa thông qua số đo của lực tác dụng lên điện tích. Lực tác dụng càng lớn tức điện tích càng lớn, lực càng nhỏ điện tích càng nhỏ, tuân theo quy luật tuyến tính:
\[F\sim q,\]
hay
\[F=kq.\tag{1}\]
với \(k\) là hệ số tỉ lệ. Mặt khác, theo định luật Newton thứ hai, lực cũng tạo ra gia tốc làm thay đổi quỹ đạo chuyển động của hạt:
\[F=ma.\tag{2}\]
Như vậy từ (1) và (2) có thể thấy điện tích \(q\) và khối lượng \(m\) của cùng một hạt có mối liên hệ rất đơn giản:
\[\frac{q}{m}=\frac{a}{k},\tag{3}\]
trong đó tỉ số \(q/m\) gọi là điện tích riêng của hạt. Việc quan sát chuyển động riêng rẽ của từng hạt mang điện tích hầu như không thể, nên hầu như không thể xác định khối lượng \(m\) một cách trực tiếp. Tuy vậy, các hạt mang điện tích lại chuyển động thành dòng với hình dạng quỹ đạo quan sát được. Gia tốc \(a\) từ đó có thể tìm được qua việc đánh giá đặc tính của quỹ đạo, còn hệ số \(k\) lấy trực tiếp từ các trường lực tác dụng. Quả thực lịch sử vật lý học đã cho thấy rằng, việc xác định tỉ số \(q/m\) đơn giản hơn nhiều so với việc đo chính điện tích \(q\) của vi hạt hoặc đo chính khối lượng \(m\) của vi hạt.
Một cách tổng quát, electron chịu tác dụng của lực Lorentz:
\[\vec{F}=-e\left(\vec{E}+\left[\vec{v}\times\vec{B}\right]\right),\]
trong đó \(e\) – điện tích electron, \(\vec{E}\) – cường độ điện trường, \(\vec{B}\) – vector cảm ứng từ, \(\vec{v}\) – vận tốc của electron. Công thức (3) viết thành:
\[\frac{e}{m}=-\frac{\vec{a}}{\vec{E}+\left[\vec{v}\times\vec{B}\right]}.\]
Độ lớn của điện trường \(\vec{E}\), từ trường \(\vec{B}\) và vận tốc \(\vec{v}\) ta có thể kiểm soát được. Gia tốc \(\vec{a}\) có thể đánh giá được thông qua đặc tính của quỹ đạo.
Trong bài thí nghiệm này, chúng ta dùng lực của một từ trường đều tác dụng lên electron:
\[F=evB.\]
Từ trường này được xếp đặt vuông góc với vận tốc ban đầu của electron, nên nó tạo nên quỹ đạo cong tròn. Từ đó ta biết được gia tốc thông qua độ cong:
\[a=\frac{v^2}{R},\]
với \(R\) – bán kính cong của quỹ đạo. Tỉ số \(e/m\) theo công thức (3) trở thành:
\[\frac{e}{m}=\frac{v^2/R}{vB}=\frac{v}{BR}.\tag{4}\]
Như vậy để tính được \(e/m\), cần biết được vận tốc \(v\) của electron, cảm ứng từ \(B\) và bán kính \(R\) của quỹ đạo tròn. Các thông số ấy sẽ có được khi làm thí nghiệm với magnetron sẽ nói bên dưới.
Magnetron
Trên hình 6.1 miêu tả cách bố trí thiết bị thí nghiệm. Trung tâm của bộ thí nghiệm là đèn chân không ba cực với cathode \(K\), anode \(A\) và lưới \(G\) đặt đồng trục với nhau. Ba nguồn điện \(U_1\), \(U_2\) và \(U_3\) lần lượt nuôi ba dòng điện sau:
– Nguồn \(U_1\) duy trì dòng đi \(I\) đi qua ống dây \(D\) (màu đậm) giúp tạo ra từ trường trong lõi ống dây. Toàn bộ đèn chân không đặt lồng trong ống dây này, xem như được đặt trong một từ trường đều vuông góc với mặt cắt hình vẽ.
– Nguồn \(U_2\) nuôi dòng điện chạy qua sợi đốt giúp đốt nóng cathode \(K\), làm phát xạ các electron từ cathode.
– Nguồn \(U_3\) tạo ra hiệu điện thế gia tốc giữa lưới \(G\) và cathode \(K\), tạo ra vận tốc ban đầu đáng kể cho các electron trước khi ra khỏi lưới để bay vào vùng nằm giữa lưới \(G\) và anode \(A\).
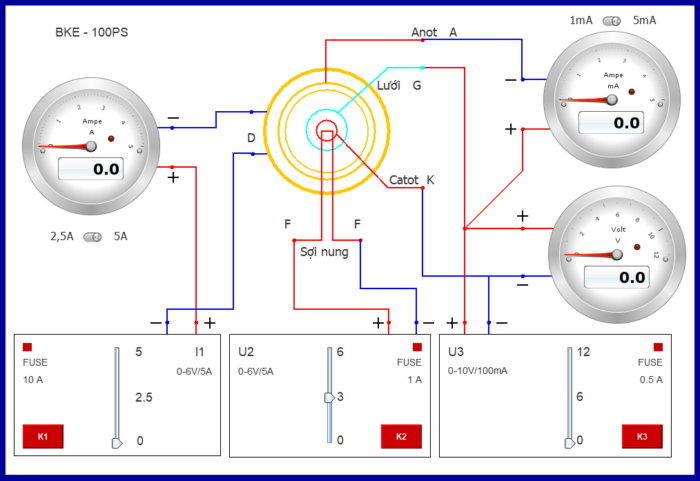
Như vậy, vùng khảo sát của chúng ta là khu vực nằm giữa lưới \(G\) và anode \(A\). Các electron có vận tốc ban đầu được tính theo động năng tích luỹ được trong quá trình gia tốc dưới hiệu điện thế \(U_3\):
\[\frac{mv^2}{2}=eU_3,\]
suy ra
\[v=\sqrt{\frac{2eU_3}{m}}.\]
Với vận tốc ban đầu này, các electron sẽ chuyển động thẳng đều từ lưới \(G\) đến anode \(A\). Ta sẽ uốn cong quỹ đạo này thành cung tròn bởi từ trường trong lõi ống dây. Từ trường này tạo ra bởi dòng điện \(I\) do nguồn \(U_1\) duy trì:
\[B=\alpha \mu_0nI,\]
với \(\mu_0\) – hằng số từ, \(n\) – số vòng dây trên một đơn vị độ dài của ống dây, \(\alpha\) – hệ số phụ thuộc vào cấu tạo của ống dây. Dòng \(I\) càng lớn, từ trường \(B\) càng lớn, quỹ đạo càng bị bẻ cong. Khi \(I\) tăng đến một giá trị giới hạn \(I_1\) nào đó thì các quỹ đạo electron sẽ cong đến mức chúng không thể bay đến anode \(A\) được nữa. Lúc ấy ta biết rằng bán kính quỹ đạo
\[R=\frac{d}{2},\]
với \(d\) là khoảng cách giữa lưới \(G\) và anode \(A\).
Thế các giá trị thực nghiệm \(v\), \(B\) và \(R\) vào (4), ta có được công thức tính điện tích riêng:
\[\frac{e}{m}=\frac{v}{BR}=\frac{8U_3}{\left(\alpha\mu_0nI_1d\right)^2}.\tag{5}\]
Quy trình thí nghiệm
Lắp đặt mạch thí nghiệm như sơ đồ hình 6.1. Đặt giá trị các hiệu điện thế \(U_1\), \(U_2\) và \(U_3\) ở mức 0.
Điện tích riêng của electron được tính theo công thức (5):
\[\frac{e}{m}=\frac{8U_3}{\left(\alpha\mu_0nI_1d\right)^2},\]
với các tham số \(n\), \(\alpha\) của ống dây và khoảng cách \(d\) giữa lưới và anode đã cho trước, điền vào bảng 6.1.
[bổ sung bảng]
Tạo hiệu điện thế gia tốc \(U_3\) giữa lưới \(G\) và cathode \(K\) ở mức 6 V, ghi vào bảng 6.2.
[bổ sung bảng]
Bắt đầu nung nóng sợi đốt bằng cách tăng dần một cách thật chậm rãi nguồn \(U_2\). Cân chỉnh sao cho dòng điện \(I_2\) từ anode \(A\) về lưới \(G\) (đo bằng ampere kế \(A_2\)) có giá trị khoảng từ 3-5 mA.
Điều chỉnh nguồn \(U_1\) tăng dần dòng \(I\) qua cuộn dây theo từng nấc một, đồng thời ghi lại giá trị dòng \(I_2\) tương ứng vào bảng 6.2.
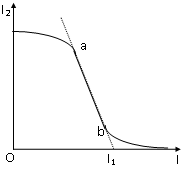
Từ bảng 6.2 ta xây dựng đồ thị phụ thuộc của \(I_2\) vào \(I\), có dạng tương tự như hình 6.2. Từ đồ thị, ta có thể lấy được giá trị \(I_1\) của dòng \(I\) khiến cho dòng \(I_2\) bị triệt tiêu. Tuy nhiên thực tế cho thấy đồ thị không cắt trục hoành một cách rõ ràng, nên ta dựng một đường \((a)-(b)\) tiếp xúc với đồ thị. Giao điểm của \((a)-(b)\) với trục hoành cho ra giá trị \(I_1\), ghi vào bảng 6.2.
Câu hỏi kiểm tra
- Định nghĩa điện tích riêng.
- Sơ đồ cấu tạo của đèn magnetron.
- Vai trò của các nguồn điện dùng trong thí nghiệm.
- Giải thích quá trình phát sinh và chuyển động của electron trong magnetron.
- Vai trò của ống dây. Công thức tính từ trường trong ống dây.
- Tác dụng của trường tĩnh điện lên điện tích. Quỹ đạo của electron khi bay qua tụ điện phẳng.
- Tác dụng của từ trường lên điện tích, lực Lorentz, độ lớn và cách xác định hướng. Quỹ đạo của electron khi chuyển động trong từ trường.
- Bán kính cong của quỹ đạo electron phụ thuộc vào tham số nào?
- Điều gì xảy ra nếu tăng cường độ dòng điện trong cuộn dây vượt qua giá trị giới hạn?
- Tại sao lực Lorentz không làm thay đổi độ lớn vận tốc của electron?
- Từ trường sinh ra bởi dòng điện, định luật Bio-Savart-Laplace.
- Chứng minh công thức tính điện tích riêng của electron:
\[\frac{e}{m}=\frac{2U}{B^2r^2},\]
trong đó \(U\) – điện áp gia tốc, \(B\) – từ trường, \(r\) – bán kính quỹ đạo tròn. - Xác định tần số chuyển động quay \(\omega\) của một điện tích \(q\), khối lượng \(m\) trong từ trường \(\vec{B}\) vuông góc với vector vận tốc.
- Xác định moment quán tính của bánh xe và lực ma sát trong ổ trục quay
- Xác định gia tốc trọng trường bằng con lắc thuận nghịch
- Xác định tỉ số nhiệt dung phân tử chất khí
- Xác định điện tích riêng electron bằng phương pháp magnetron
- Xác định giá trị điện trở, điện dung, độ tự cảm bằng phương pháp dao động điện cưỡng bức
- Nhiễu xạ ánh sáng
- Khảo sát hiện tượng bức xạ nhiệt và kiểm chứng định luật Stefan-Boltzmann
- Khảo sát hiệu ứng quang điện ngoài. Xác định giá trị hằng số Planck
- Khảo sát đặc tuyến volt-ampere của diode và transistor