Nhiễu xạ ánh sáng
Chương trình máy tính “Nhiễu xạ ánh sáng” – viết bằng ngôn ngữ java – miêu tả trực quan sự hình thành phổ nhiễu xạ của ánh sáng qua cách tử. Ngoài ra chương trình cũng cho phép tiến hành thí nghiệm ảo với mô hình giao thoa hai khe kinh điển, một trường hợp riêng của giao thoa – nhiễu xạ nhiều khe.
Bài viết dưới đây trình bày về thí nghiệm xác định bước sóng của một chùm sáng đơn sắc nhờ vào hiện tượng nhiễu xạ trên cách tử và đo đường kính sợi dây mảnh bằng phương pháp nhiễu xạ.
Chương trình mô phỏng thực hiện bởi sinh viên
ngành Công nghệ thông tin
Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh:
Lê Minh Hổ – Võ Huy Hoàng – Phạm Thái Vĩnh
Nguyễn Anh Sang – Bùi Công Hiếu – Lê Thanh Hiếu
Để tìm hiểu thêm, có thể xem chương trình mô phỏng và bài viết riêng về hiện tượng nhiễu xạ.
Lưu ý: chương trình chạy trên nền java
Video minh hoạ
Nguyên lý phép đo
Nhiễu xạ trên cách tử
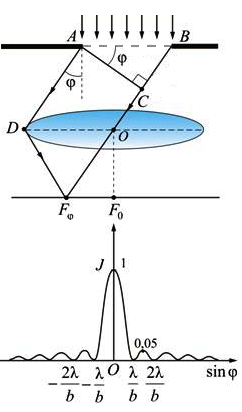
Trong bài thí nghiệm này, chúng ta muốn đo độ dài của bước sóng ánh sáng ứng với một màu đơn sắc (hình 1). Theo nguyên tắc chung của mọi phép đo, ta phải tìm cách sao cho đại lượng cần đo, đại lượng mà ta chưa biết, đi so sánh với một “vật” cùng bậc về kích cỡ mà ta đã biết. Vật đó có thể xem như thước đo. Vật cần đo phải cho tương tác, bắn phá… vào vật làm thang đo. Muốn đo một đối tượng lớn, ta cần một cây thước lớn. Muốn đo một đối tượng nhỏ, ta cần một cây thước nhỏ.
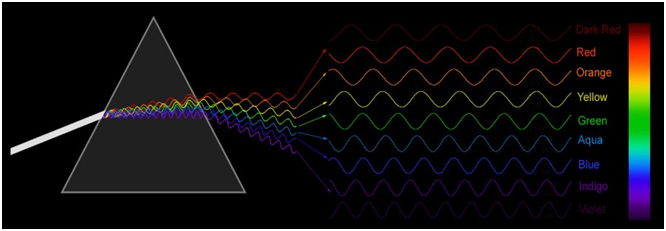
Ánh sáng lại có bước sóng rất nhỏ. Trong dải ánh sáng nhìn thấy, nó có giá trị khoảng từ 0.4 đến 0.8 \(\mu\)m. Để xác định bước sóng của một màu ánh sáng đơn sắc nào đó, ta cũng cần loại thước đo có vạch chia nhỏ tương ứng. Thước đo chúng ta sử dụng trong thí nghiệm này chính là cách tử.
Cách tử là một hệ quang học, trên bề mặt khắc lên những vạch đều đặn song song. Đặc trưng chính của cách tử chính là khoảng cách \(d\) giữa hai vạch liên tiếp, hay còn gọi là chu kì của cách tử, chỉ lớn hơn bước sóng cần đo khoảng vài chục đến vài trăm lần, đóng vai trò như vạch chia của thước đo ánh sáng.
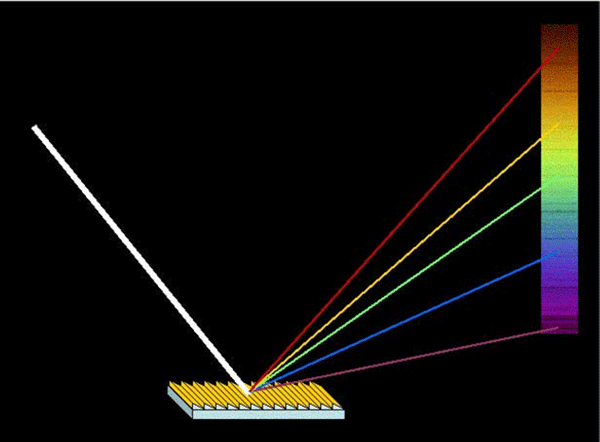
Có hai loại cách tử chính: cách tử phản xạ và cách tử truyền qua. Trên hình 2 biểu diễn phản ứng của nhiều ánh sáng có bước sóng khác nhau trên bề mặt cách tử phản xạ. Các màu đơn sắc khác nhau tạo những góc lệch khác nhau. Biết được chu kì của cách tử, đồng thời đo được góc lệch của tia sáng, ta có thể đánh giá về bước sóng của ánh sáng chiếu đến.
Bài thí nghiệm của chúng ta thực hiện trên cách tử truyền qua, có thể hình dung như tập hợp rất nhiều khe hẹp song song. Hình 3 thể hiện bức tranh nhiễu xạ trong nhiều trường hợp số khe khác nhau: \(N=2\), \(N=4\), \(N=8\), \(N=16\).
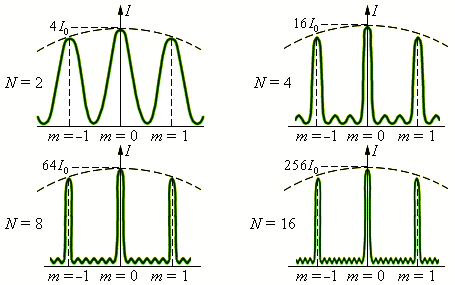
Tính toán lý thuyết cho thấy rằng, hình ảnh nhiễu xạ qua cách tử rải ra thành các cực đại chính, giữa hai cực đại chính liên tiếp xuất hiện thêm các cực đại phụ. Với hệ cách tử làm từ \(N\) khe sẽ tạo ra \(N-2\) cực đại phụ xen giữa mỗi cặp cực đại chính liên tiếp. Vấn đề cực tiểu chính và cực tiểu phụ chúng ta không bàn đến và cũng không ảnh hưởng đến thí nghiệm.
Trên thực tế số khe \(N\) của cách tử rất lớn, do đó các cực đại phụ trở nên mờ nhạt không đáng kể, còn các cực đại chính trở nên nổi bật, sắc nét. Vì thế trong bài thí nghiệm chúng ta đo khoảng cách giữa các cực đại chính. Trên hình 4 là sơ đồ dụng cụ thí nghiệm, bao gồm nguồn tia lazer, cách tử và màn quan sát.
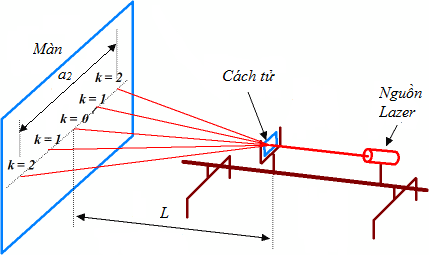
Cực đại chính xuất hiện là do sự đồng pha giữa các nguồn thứ cấp chuyển đến từ mỗi khe:
\[d\sin\varphi_k=\pm k\lambda,\qquad k=0, 1,2,\dots\]
trong đó \(\lambda\) – bước sóng cần đo. \(k=0\) tương ứng với cực đại chính trung tâm, \(k=1\) tương ứng với cực đại chính bậc 1, v.v…, \(\varphi_k\) là góc lệch của cực đại chính bậc \(k\). Góc lệch \(\varphi_k\) có được nhờ phép đo hình học
\[\sin\varphi_k\approx\tan\varphi_k=\frac{a_k}{2L},\]
với \(a_k\) – khoảng cách giữa hai cực đại chính bậc \(k\), \(L\) khoảng cách từ cách tử đến màn. Từ đây ta có công thức xác định bước sóng:
\[\lambda=\frac{d}{k}\cdot\frac{a_k}{2L}.\tag{1}\]
Công thức (1) có ý nghĩa vật lý như sau: khoảng cách từ cách tử đến màn lớn hơn độ lệch của vân cực đại chính bậc nhất khỏi hướng ban đầu bao nhiêu lần, thì chu kì của cách tử sẽ lớn hơn bước sóng ánh sáng bấy nhiêu lần. Cho dễ hình dung, chỉ cần viết lại (1) theo dạng tỉ lệ dành cho cực đại chính bậc nhất:
\[\frac{\lambda}{d}=\frac{a_1/2}{L}.\]
Ý nghĩa vật lý này giải thích tại sao chu kì \(d\) của cách tử cần có kích thước lớn hơn độ dài của bước sóng cần đo khoảng từ vài chục lần đến vài trăm lần. Nếu chu kì \(d\) cùng độ rộng các rãnh quá lớn, vượt quá nghìn lần bước sóng, hiệu ứng nhiễu xạ sẽ suy yếu và ánh sáng trở nên truyền thẳng theo kiểu quang hình học. Còn nếu chu kì \(d\) quá nhỏ, giảm xuống cùng bậc với bước sóng, sóng điện từ sẽ không thể truyền qua lưới.
Nhiễu xạ trên khe
Trong phần hai của bài thí nghiệm chúng ta sẽ đo đường kính của một sợi dây mảnh cỡ như sợi tóc. Cụ thể ta sẽ tiến hành trên sợi tóc thực. Sợi tóc có kích thước rất bé, đường kính chỉ nằm trong khoảng từ 40 đến 120 \(\mu\)m. Trong khi đó thước kẹp có sai số lên đến 20 \(\mu\)m (\(0{.}02\) mm), không thể áp dụng cho trường hợp này.
Có những phương pháp khác nhau để tiến hành phép đo này. Ở đây ta sử dụng phép đo dựa trên hiện tượng nhiễu xạ ánh sáng khi đi qua vật cản. Sợi tóc cũng như khe hẹp, là những vật cản có kích thước chỉ lớn hơn bước sóng ánh sáng từ vài chục đến vài trăm lần. Do đó định luật truyền thẳng trong quang hình học không còn đúng nữa. Sóng lan truyền bị bẻ cong khỏi phương truyền ban đầu một cách rõ nét khi đi qua các vật cản này. Quan sát đặc tính của bức tranh nhiễu xạ trên màn, biết trước độ dài của bước sóng ánh sáng sử dụng, ta có thể suy ra được kích thước của vật cản.
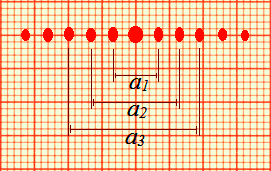
Bức tranh nhiễu xạ trên sợi tóc có cấu tạo hoàn toàn tương đồng với trường hợp nhiễu xạ trên khe, nếu khe có độ rộng đúng bằng đường kính sợi tóc. Do vậy lý thuyết nhiễu xạ trên sợi dây có thể quy về lý thuyết nhiễu xạ trên khe hẹp, minh hoạ trên hình 5.
Vị trí các điểm cực tiểu được xác định theo công thức:
\[b\sin\varphi_k=\pm k\lambda,\qquad k=1,2,\dots\]
trong đó \(b\) – độ rộng của khe (hoặc đường kính của sợi tóc). Các góc \(\varphi_k\) có thể tìm được qua phép đo hình học:
\[\sin\varphi_k\approx\tan\varphi_k=\frac{x_k}{L},\]
với \(x_k\) – vị trí cực tiểu thứ \(k\) ở trên màn, \(L\) – khoảng cách từ khe (hoặc sợi tóc) đến màn. Từ đây ta có công thức xác định đường kính sợi tóc:
\[b=k\lambda\cdot\frac{L}{x_k}.\tag{2}\]
Công thức (2) có ý nghĩa vật lý như sau: khoảng cách từ sợi tóc đến màn quan sát lớn hơn độ phân kì của tia sáng bao nhiêu lần, thì đường kính của sợi tóc sẽ lớn hơn bước sóng ánh sáng bấy nhiêu lần. Cho dễ hình dung, chỉ cần viết lại (2) theo dạng tỉ lệ cho trường hợp \(k=1\):
\[\frac{b}{\lambda}=\frac{L}{a_1}.\]
Từ đây ta có thể thấy rằng, hiện tượng nhiễu xạ trên vật cản chỉ trở nên rõ nét khi kích thước vật cản chỉ lớn hơn bước sóng từ vài chục đến vài trăm lần. Nếu vật cản quá lớn so với bước sóng, sóng sẽ lan truyền gần như theo đường thẳng.
Quy trình thí nghiệm
Đo bước sóng ánh sáng qua nhiễu xạ trên cách tử
Bật bộ phát lazer, thiết lập hệ nhiễu xạ qua cách tử, sao cho bức tranh nhiễu xạ có thể quan sát được trên màn có vạch chia mm như hình 6. Có thể sử dụng giấy vở đóng vai trò của màn. Chụp ảnh lại hệ nhiễu xạ cho dễ quan sát rồi vẽ lại trên giấy mm.
Bước sóng của chùm sáng được tính theo công thức (1)
\[\lambda=d\cdot\frac{a_k}{2kL},\]
trong đó chu kì \(d\) của cách tử là tham số cho trước, ghi vào bảng 1.
[bổ sung bảng]
Khoảng cách \(L\) từ cách tử đến màn quan sát xác định bằng thước trên thanh trượt. Ghi giá trị \(L\) vào bảng thực nghiệm 2.
Khoảng cách \(a_k\) giữa hai cực đại chính bậc \(k\), nằm đối xứng hai bên vân sáng trung tâm, xác định theo như hướng dẫn trên hình 6. Giá trị thu được ghi vào bảng thực nghiệm 2. Phép đo tiến hành với ít nhất 3 cặp cực đại chính.
[bổ sung bảng]
Đo bước đường kính sợi tóc bằng phương pháp nhiễu xạ
Quay giá đỡ cách tử sang một bên sao cho tia lazer đi thẳng đến màn, không còn bị cản trở bởi cách tử. Đặt sợi tóc ngay trước đèn lazer, sao cho bức tranh nhiễu xạ có thể quan sát được trên màn có vạch chia mm như hình 7. Có thể sử dụng giấy vở đóng vai trò của màn. Chụp ảnh lại hệ nhiễu xạ cho dễ quan sát rồi vẽ lại trên giấy mm.
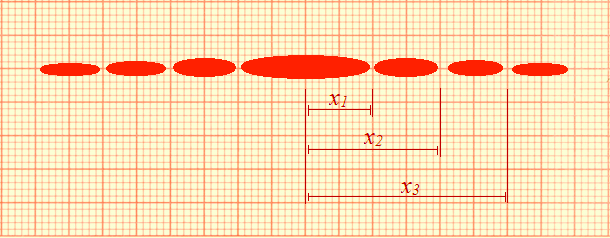
Đường kính của sợi được tính theo công thức (2)
\[b=k\lambda\cdot\frac{L}{x_k},\]
trong đó bước sóng \(\lambda\) của chùm tia lazer đã có được từ phần thí nghiệm trước.
Khoảng cách \(L\) từ sợi tóc đến màn quan sát xác định bằng thước trên thanh trượt. Ghi giá trị \(L\) vào bảng 3.
Toạ độ \(x_k\) của những cực tiểu tính từ tâm của cực đại trung tâm, như hướng dẫn trên hình 7, ghi vào bảng 3. Phép đo tiến hành với ít nhất 3 cực tiểu.
[bổ sung bảng]
Phần mềm mô phỏng
Ứng dụng mô phỏng được thiết kế giúp người dùng dễ hình dung được toàn cảnh bức tranh nhiễu xạ. Giao diện phần mềm có dạng như hình 1. Bảng điều khiển thực hiện mô phỏng trên hai loại vật cản chính: cách tử và khe, phông nền sáng và phông nền tối. Trường hợp vật cản như sợi dây mảnh cũng có bức tranh nhiễu xạ tương tự nhiễu xạ qua khe.
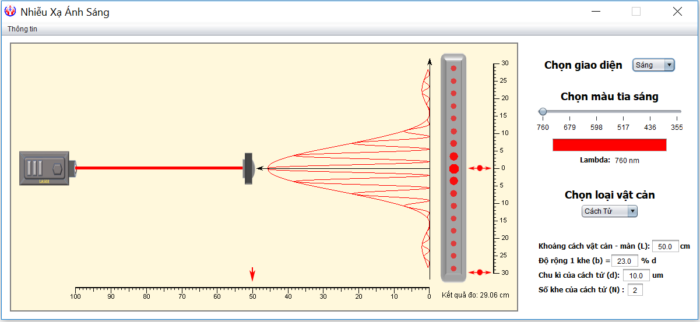
Với trường hợp cách tử, các tham số cần thiết lập gồm:
– Khoảng cách \(L\) giữa cách tử và màn, bằng cách dùng chuột kéo vật dọc theo thanh trượt.
– Chu kỳ \(d\) của cách tử.
– Độ rộng của một khe, tính bằng đơn vị phần trăm so với chu kỳ \(d\).
– Số khe \(N\) của cách tử.
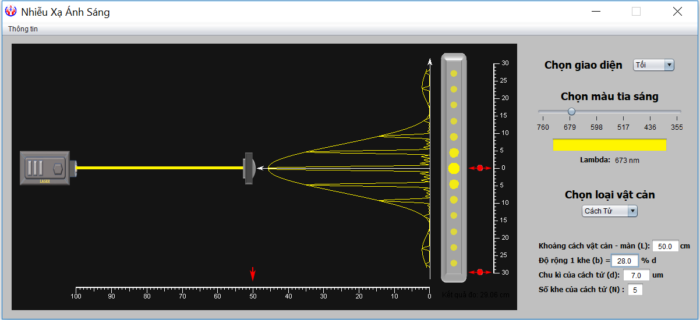
Với trường hợp của khe, các tham số thiết lập gồm:
– Khoảng cách \(L\) giữa khe và màn, bằng cách dùng chuột kéo vật dọc theo thanh trượt.
– Kích thước của khe.
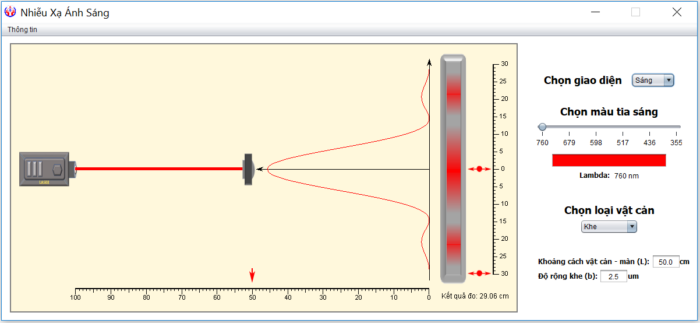
Bức tranh nhiễu xạ sẽ thay đổi sinh động khi ta trực tiếp thay đổi màu sắc của chùm sáng chiếu đến, cũng như thay đổi khoảng cách giữa màn.
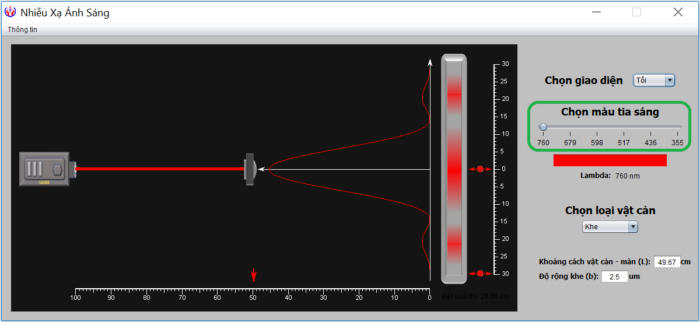
Câu hỏi kiểm tra
- Khái niệm ánh sáng đơn sắc, ánh sáng không đơn sắc.
- Mối liên hệ giữa màu sắc và bước sóng. Nguyên nhân tạo ra màu sắc khi quan sát vật thể. Phân biệt màu đơn sắc và màu không đơn sắc.
- Viết phương trình lan truyền của một sóng phẳng đơn sắc. Chỉ rõ biên độ, pha, chu kỳ, bước sóng.
- Khái niệm về hiện tượng nhiễu xạ. Phân biệt nhiễu xạ với khúc xạ và phản xạ. Điều kiện nào thì hiện tượng nhiễu xạ trở nên rõ nét?
- Khái niệm về cách tử. Đại lượng đặc trưng cho cách tử.
- Bước sóng của các loại ánh sáng nhìn thấy nằm trong khoảng nào? So sánh với bước sóng của tử ngoại, hồng ngoại, sóng radio.
- Tại sao chu kì của cách tử trong bài thí nghiệm không được quá lớn, nó chỉ được phép lớn hơn bước sóng từ vài chục đến vài trăm lần?
- Trong bài thí nghiệm thay vì đo đường kính sợi tóc với kích thước ước chừng trong khoảng từ 40 – 120 \(\mu\)m, liệu có thể dùng phương pháp đó để đo đường kính của sợi dây thép, dây đàn, dây điện… được không?
- Tại sao ánh sáng chiếu qua cửa sổ, ta xem rằng ánh sáng truyền thẳng và tạo bóng, còn khi chiếu qua khe hẹp ta lại không xem rằng ánh sáng truyền thẳng mà truyền cong do nhiễu xạ?
- Sóng điện thoại có tần số bằng bao nhiêu? Tính bước sóng của nó. Tại sao ta có thể dùng điện thoại để liên lạc với nhau? Vai trò của nhiễu xạ trong liên lạc vô tuyến? Tại sao trong liên lạc bằng điện thoại di động hiện đại, ta sử dụng các tần số nói trên, không cao hơn cũng không thấp hơn?
- Tần số của sóng âm của sóng âm thuộc dải nghe thấy bằng bao nhiêu? Tính bước sóng của sóng âm thuộc dải nghe thấy. Tại sao ta không thể nhìn thấy một người ở bên kia tấm chắn, nhưng vẫn nghe thấy âm thanh nói chuyện của họ?
- Tại sao dùng cách tử có thể phân biệt được hai chùm sáng đơn sắc có bước sóng khác nhau?
Viết và chứng minh công thức tính bước sóng dựa trên hiện tượng nhiễu xạ qua cách tử. - Phát biểu nguyên lý Huygens-Fresnel. Diễn tả quá trình truyền sóng theo quan điểm Huygens-Fresnel.
- Sử dụng nguyên lý Huygens-Fresnel để giải thích hiện tượng khúc xạ ánh sáng trên mặt phân cách giữa hai môi trường.
- Xác định moment quán tính của bánh xe và lực ma sát trong ổ trục quay
- Xác định gia tốc trọng trường bằng con lắc thuận nghịch
- Xác định tỉ số nhiệt dung phân tử chất khí
- Xác định điện tích riêng electron bằng phương pháp magnetron
- Xác định giá trị điện trở, điện dung, độ tự cảm bằng phương pháp dao động điện cưỡng bức
- Nhiễu xạ ánh sáng
- Khảo sát hiện tượng bức xạ nhiệt và kiểm chứng định luật Stefan-Boltzmann
- Khảo sát hiệu ứng quang điện ngoài. Xác định giá trị hằng số Planck
- Khảo sát đặc tuyến volt-ampere của diode và transistor