Xác định gia tốc trọng trường bằng con lắc thuận nghịch
Chương trình máy tính “Con lắc thuận nghịch” mô phỏng lại gần như chính xác nguyên lý hoạt động của thiết bị cùng tên trên thực tế. Con lắc thuận nghịch thường bắt gặp trong các phòng thí nghiệm của nhà trường, với mục đích xác định gia tốc rơi tự do với độ chính xác cao.
Chương trình mô phỏng thực hiện bởi sinh viên
ngành Công nghệ thông tin
Đại học Sư phạm Kỹ thuật Tp. Hồ Chí Minh:
Liên Minh Quang
Minh hoạ mô phỏng con lắc
Mô tả chương trình
Chương trình mô phỏng thực hiện theo một con lắc khác với quả nặng lớn hơn nhằm mục đích minh hoạ rõ nét sự thay đổi các tham số của con lắc như: vị trí trọng tâm, chu kì dao động, chiều dài rút gọn… Khi ấy người xem sẽ dễ hiểu được cơ chế làm việc của con lắc hơn. Người dùng có thể dùng chuột thay bàn tay vặn quả nặng lên xuống, thay đổi trục quay của con lắc, dùng chuột kéo con lắc ra góc lệch ban đầu và cho dao động.
Con lắc này có cấu tạo từ:
– Một thanh đồng chất dài 1.2 m, khối lượng 1 kg.
– Hai lưỡi dao \(O_1O_2\) gắn cố định, mỗi cái khối lượng 100 g. Một lưỡi dao cách đầu thanh 10 cm, hai lưỡi dao lại cách nhau 71.5 cm.
– Hai quả nặng, khối lượng mỗi quả 2 kg, độ dày 2 cm. Một quả gắn cố định vào điểm nằm giữa hai lưỡi dao, cách dao \(O_1\) 15 cm. Quả nặng kia gắn phía ngoài \(O_2\) và có thể vặn di chuyển được.

Đặc biệt chương trình còn biểu diễn con lắc đơn tương ứng có cùng chu kì dao động. Điều này nhằm diễn đạt một cách hình ảnh khái niệm “chiều dài rút gọn” của con lắc vật lý. Khi dùng chuột thay bàn tay vặn quả nặng, chiều dài này được biểu diễn qua dấu mũi tên.
Nếu chiều dài rút gọn này không bằng khoảng cách \(O_1O_2\), chu kì dao động qua trục \(O_1\) và qua trục \(O_2\) sẽ khác nhau. Còn nếu chiều dài rút gọn trùng với khoảng cách \(O_1O_2\), con lắc sẽ dao động với chu kì như nhau dù treo ở đầu nào.
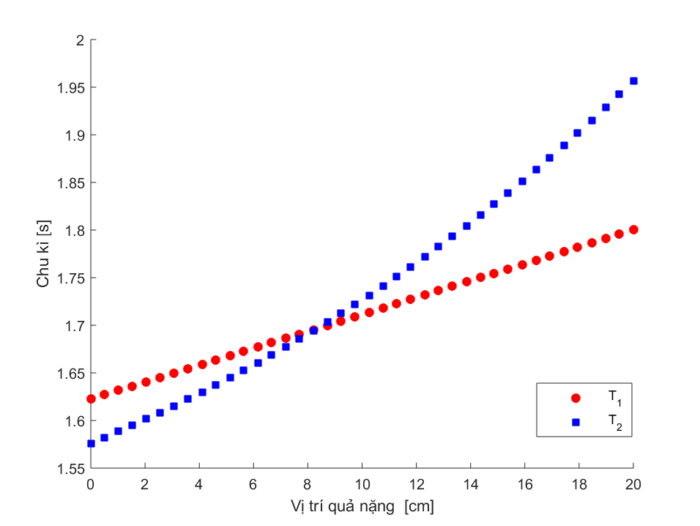
Chu kì của con lắc mô phỏng này phụ thuộc vào vị trí quả nặng di động như đồ thị dưới. Giao điểm của hai đồ thị chu kì tương ứng với vị trí quả nặng, khi sự kiện chiều dài rút gọn trùng với khoảng cách \(O_1O_2\) xảy ra.
Nguyên lý mô phỏng
Nguyên lý hoạt động con lắc thuận nghịch
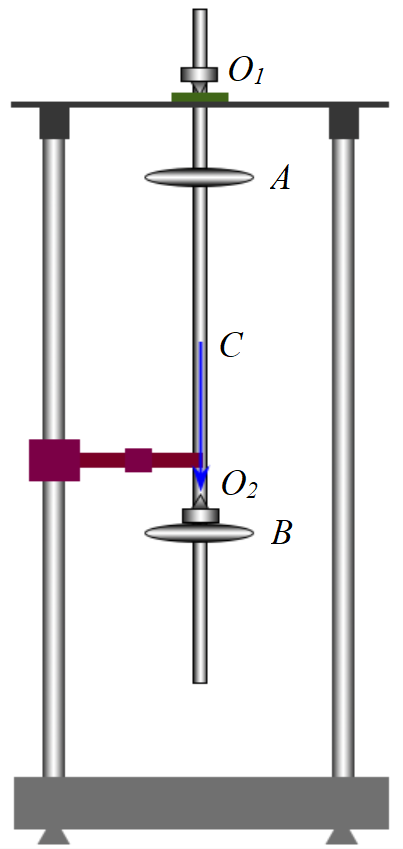
Con lắc thuận nghịch là con lắc có đến hai điểm treo: \(O_1\) và \(O_2\), vít cố định như hình 2.1. Ta có thể treo con lắc dao động quanh một trong hai điểm đó, khi ấy con lắc dao động như một con lắc vật lý thông thường với chu kỳ:
\[T=2\pi\sqrt{\frac{I}{mga}},\tag{1}\]
trong đó \(I\) – moment quán tính của con lắc đối với trục đi qua điểm treo, \(a\) – khoảng cách từ trọng tâm đến điểm treo. Nhớ lại rằng chu kỳ dao động của con lắc toán học có dạng:
\[T=2\pi\sqrt{\frac{l}{g}}.\]
So sánh hai công thức trên, đặt
\[L=\frac{I}{ma}.\]
Thế vào (1) ta có:
\[T=2\pi\sqrt{\frac{L}{g}}.\tag{2}\]
Ta gọi \(L\) là chiều dài rút gọn của con lắc vật lý. Đó là chiều dài của một con lắc toán học có chu kỳ trùng với con lắc vật lý đang xét.
Như vậy từ công thức (2), nếu biết được chu kỳ \(T\) và chiều dài rút gọn \(L\), ta có thể suy ra được gia tốc trọng trường \(g\) cần tìm. Vấn đề không đơn giản, bởi vì ta chưa xác định được độ dài rút gọn.
Các chứng minh phức tạp hơn dẫn đến kết quả rất quan trọng như sau: nếu treo ngược con lắc và cho nó dao động quanh điểm \(O_2\) mà chu kỳ dao động của nó vẫn không đổi, thì khoảng cách \(O_1O_2\) giữa hai điểm treo chính bằng chiều dài rút gọn \(L\).
Hay:
Nếu
\[T’=T,\]
thì
\[L=O_1O_2.\]
Vậy nên để đi tìm độ dài rút gọn \(L\), ta cần điều chỉnh cấu trúc của con lắc sao cho dù treo ở \(O_1\) hay \(O_2\), chu kỳ dao động của nó vẫn như nhau. Con lắc thuận nghịch trong bài thí nghiệm được cấu tạo có chủ ý, sao cho trọng tâm của nó thay đổi được nhờ di chuyển quả nặng \(B\) (nằm ngoài đoạn thẳng \(O_1O_2\)).
Những suy luận trên dẫn đến nguyên tắc tiến hành thí nghiệm khá đơn giản như sau. Điều chỉnh quả nặng \(B\) đến vị trí thích hợp sao cho khi đo chu kỳ dao động qua \(O_1\) và \(O_2\) cho ra cùng một giá trị chu kỳ \(T\). Từ đó tính được gia tốc trọng trường theo công thức (2)
\[g=\frac{4\pi^2L}{T^2}=\frac{4\pi^2O_1O_2}{T^2}.\]
Con lắc thuận nghịch trên thực tế
- Xác định moment quán tính của bánh xe và lực ma sát trong ổ trục quay
- Xác định gia tốc trọng trường bằng con lắc thuận nghịch
- Xác định tỉ số nhiệt dung phân tử chất khí
- Xác định điện tích riêng electron bằng phương pháp magnetron
- Xác định giá trị điện trở, điện dung, độ tự cảm bằng phương pháp dao động điện cưỡng bức
- Nhiễu xạ ánh sáng
- Khảo sát hiện tượng bức xạ nhiệt và kiểm chứng định luật Stefan-Boltzmann
- Khảo sát hiệu ứng quang điện ngoài. Xác định giá trị hằng số Planck
- Khảo sát đặc tuyến volt-ampere của diode và transistor