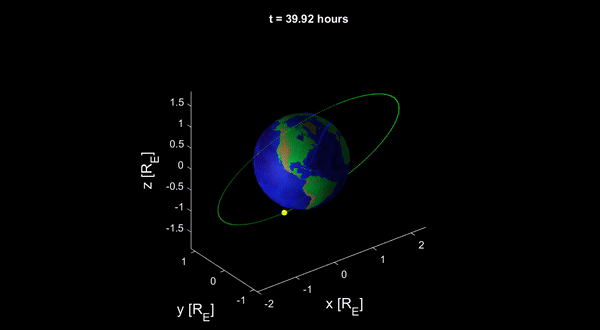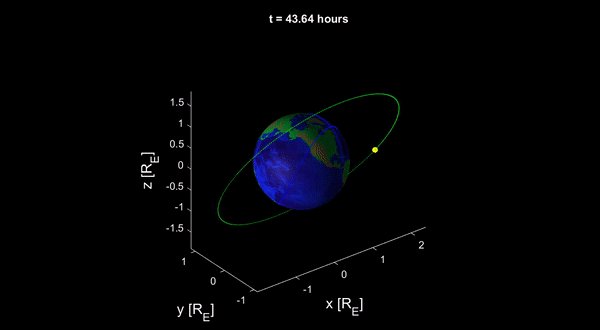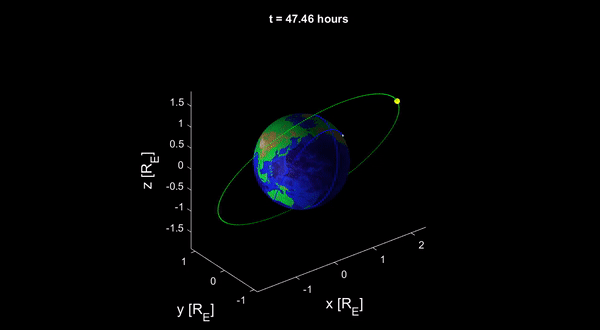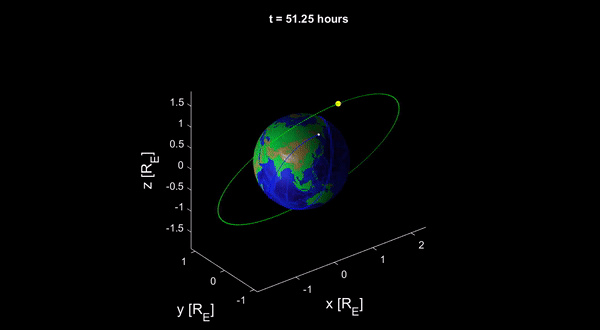
Vệ tinh chuyển động trong trường hấp dẫn Trái đất chịu tác dụng của một gia tốc:
\[\vec{a}=-\frac{GM}{r^3}\cdot\vec{r},\]
trong đó \(G\) – hằng số hấp dẫn, \(M\) – khối lượng Trái đất, \(\vec{r}\) – vector toạ độ của vệ tinh. Trạng thái ban đầu của vệ tinh được cho dưới dạng toạ độ Descartes:
1 2 | r = [-2*R_earth 0 0]; % x, y, z v = [0 -3e3 5e3]; % vx, vy, vz |
Trong vòng lặp tính toán sự tiến hoá của trạng thái theo thời gian, chỉ cần biết trạng thái ban đầu, vận tốc và toạ độ tại mọi thời điểm sau đó được tính toán theo định nghĩa:
1 2 3 4 5 6 7 8 9 10 |
Để thiết lập các loại quỹ đạo trong thực tế kĩ thuật, ta cần biết trước chu kì chuyển động \(T\) của vệ tinh. Ví dụ vệ tinh trên các quỹ đạo đồng bộ, tính cả quỹ đạo địa tĩnh, có chu kì quay bằng đúng chu kì tự quay quanh trục của Trái đất, tức 23 giờ 56 phút 4 giây, ngắn hơn ngày trung bình khoảng 4 phút. Thời gian đi hết một phòng quỹ đạo của vệ tinh Molnya lại chỉ bằng một nửa: 11 giờ 57 phút 45 giây.
Theo định luật Kepler thứ ba, lập phương bán trục lớn tỉ lệ với bình phương chu kì chuyển động theo quỹ đạo. Từ đó ta có thể tính được giá trị bán trục lớn:
\[a=\sqrt[3]{\frac{GMT^2}{4\pi^2}}.\]
Năng lượng toàn phần của vệ tinh gắn liền với bán trục lớn:
\[E=-\frac{GM}{2a}.\]
Trong chương trình này, vệ tinh được tạo vận tốc đầu tại cận điểm quỹ đạo, nằm cách tâm Trái đất một đoạn bằng
\[r_0=a(1-e),\]
trong đó \(e\) là tâm sai được cho trước. Với quỹ đạo địa tĩnh, elip trở thành đường tròn với tâm sai \(e=0\), bán trục lớn trở thành bán kính \(r_0=a\). Ở Liên xô và Nga do phân bố lãnh thổ trên các vĩ độ cao, người ta phát triển những loại quỹ đạo elip có tâm sai lớn, như vệ tinh Molnya và Tundra, sao cho viễn điểm nằm ngay trên đỉnh trời. Theo định luật Kepler thứ hai, vệ tinh đi qua viễn điểm khá chậm, làm tăng thời gian hiện diện của chúng trên các vĩ độ cao. Ưu điểm khác của các loại vệ tinh này là lượng quỹ đạo phong phú hơn nhiều so với quỹ đạo địa tĩnh.
Vận tốc ban đầu của vệ tinh có thể tính được qua hệ thức bảo toàn cơ năng:
\[v=\sqrt{2\left(\frac{GM}{r_0}+E\right)}.\]
Trên Matlab, trạng thái ban đầu của vệ tinh với quỹ đạo có chu kì, tâm sai và độ nghiêng cho trước được tính toán một cách tổng quát như sau, ví dụ cho trường hợp quỹ đạo Molnya:
1 2 3 4 5 6 7 8 9 | T_Molnya = 11<em>3600+57</em>60+45; % Chu ki quay cua ve tinh e = 0.73; % Tam sai a = (G<em>M</em>T_Molnya^2/4/pi^2)^(1/3); % Ban truc lon quy dao elip E = -G<em>M/2/a; % Nang luong toan phan r0 = a</em>(1-e); v0 = sqrt(2<em>(G</em>M/r0+E)); alpha = 63.4/180<em>pi; r = [-r0</em>cos(alpha) 0 -r0*sin(alpha)]; v = [0 -v0 0]; |
Vết quỹ đạo (tiếng Anh: ground track, tiếng Nga: трасса орбита), tức hình chiếu của quỹ đạo vệ tinh lên bề mặt Trái đất được tìm qua giao điểm của vector bán kính toạ độ và mặt cầu bán kính \(R_E=6370\) km:
\[\vec{r_{gt}}=\frac{\vec{r}}{r}R_E,\]
trong đó \(R_E\) – bán kính Trái đất. Nhờ theo dõi vết quỹ đạo, ta có thể phân biệt đánh giá tác dụng của mỗi loại quỹ đạo.
Video minh hoạ
Code chương trình
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 | function chuyendongvetinh_3D_new % Created by Tran Hai Cat % 2017.10.17 clc; clear all; close all; %% CONSTANTS G = 6.67e-11; % Hang so hap dan M = 5.97219e24; % Khoi luong Trai dat R_earth = 6371e3; % Ban kinh Trai dat T = 23*3600+56*60+4; % Chu ki quay quanh truc: 23 gio 56 phut 4 giay %% INPUT DATA phi = -105; r = [-2*R_earth 0 0]; v = [0 -3e3 5e3]; N_orbit = 500; N_ground_track = 500; dt = 50; %% Geostationary orbit (Quy dao dia tinh): % phi = -105; % e = 0.0; % Tam sai, e = 0 tuong ung voi quy dao tron % a = (G*M*T^2/4/pi^2)^(1/3); % Ban truc lon quy dao elip % E = -G*M/2/a; % Nang luong toan phan % r0 = a*(1-e); % r = [-r0 0 0]; % v0 = sqrt(2*(G*M/r0+E)); % alpha = 0; % r = [-r0*cos(alpha) 0 -r0*sin(alpha)]; % v = [0 -v0 0]; % N_orbit = 1000; % N_ground_track = 900; % dt = 100; % %% Geosynchronous orbit (Quy dao dong bo) % phi = -60; % e = 0; % Tam sai % a = (G*M*T^2/4/pi^2)^(1/3); % Ban truc lon quy dao elip % E = -G*M/2/a; % Nang luong toan phan % r0 = a*(1-e); % v0 = sqrt(2*(G*M/r0+E)); % alpha = 63.4/180*pi; % r = [-r0*cos(alpha) 0 -r0*sin(alpha)]; % v = [0 -v0 0]; % N_orbit = 1000; % N_ground_track = 900; % dt = 100; % %% Tundra orbit % phi = -60; % T_Tundra = T; % e = 0.3; % Tam sai % a = (G*M*T_Tundra^2/4/pi^2)^(1/3); % Ban truc lon quy dao elip % E = -G*M/2/a; % Nang luong toan phan % r0 = a*(1-e); % v0 = sqrt(2*(G*M/r0+E)); % alpha = 63.4/180*pi; % r = [-r0*cos(alpha) 0 -r0*sin(alpha)]; % v = [0 -v0 0]; % N_orbit = 1500; % N_ground_track = 1700; % dt = 50; % %% Molnya orbit % phi = -15; % T_Molnya = 11*3600+57*60+45; % e = 0.73; % Tam sai % a = (G*M*T_Molnya^2/4/pi^2)^(1/3); % Ban truc lon quy dao elip % E = -G*M/2/a; % Nang luong toan phan % r0 = a*(1-e); % v0 = sqrt(2*(G*M/r0+E)); % alpha = 63.4/180*pi; % r = [-r0*cos(alpha) 0 -r0*sin(alpha)]; % v = [0 -v0 0]; % N_orbit = 1000; % N_ground_track = 1500; % dt = 50; %% Xu ly d = 5; t = 0; L = 1; dphi = 360*dt/T; dphi_rad = 2*pi*dt/T; cosdphi = cos(dphi_rad); sindphi = sin(dphi_rad); orbit_array = zeros(3,N_orbit); orbit_array(:,end) = r/R_earth; R_2 = sum(r.^2); R = sqrt(R_2); ground_track = r./R; ground_track_array = zeros(3,N_ground_track); ground_track_array(:,end) = ground_track; %% DRAW EARTH load('topo.mat','topo','topomap1'); [x1,y1,z1] = sphere(50); x1 = 1*x1; y1 = 1*y1; z1 = 1*z1; props.AmbientStrength = 0.2; props.DiffuseStrength = 0.7; props.SpecularColorReflectance = .5; props.SpecularExponent = 5; props.SpecularStrength = .1; props.FaceColor= 'texture'; props.EdgeColor = 'none'; props.FaceLighting = 'gouraud'; props.Cdata = topo; %% FIGURE figure('name','Sputnik','color','black','numbertitle','off'); % set(gcf,'Units','normalized'); % set(gcf,'Position',[0 0.05 1.0 1.0]); set(gca,'color','black','xcolor','w','ycolor','w','zcolor','w') colormap(topomap1); hold on fig_earth = surface(x1,y1,z1,props); fig_light = light('position',[-1 0 0]); hf = plot3(orbit_array(1,end),orbit_array(2,end),orbit_array(3,end),'yo','markersize',d,'markerfacecolor','y'); hf_orbit = plot3(orbit_array(1,:),orbit_array(2,:),orbit_array(3,:),'wo','markersize',1); hf_ground_track = plot3(ground_track_array(1,:),ground_track_array(2,:),ground_track_array(3,:),'bo','markersize',1); hf_ground_track_end = plot3(ground_track_array(1,end),ground_track_array(2,end),ground_track_array(3,end),'wo','markersize',2,'markerfacecolor','w'); ht = title(sprintf('t = %0.2f s',t),'color','w'); axis equal axis([-inf inf -inf inf -inf inf]); view(3); rotate3d on xlabel('x [R_E]','fontsize',14); ylabel('y [R_E]','fontsize',14); zlabel('z [R_E]','fontsize',14); %% CALCULATION while 1 t = t+dt; phi = mod(phi+dphi,360); topoc = topo(:,1:360-round(phi)); topoc = [topo(:,361-round(phi):end),topoc]; R_2 = sum(r.^2); R = sqrt(R_2); a = -G*M/R^3*r; v = v+a*dt; r = r+v*dt; orbit_array(:,1:end-1) = orbit_array(:,2:end); orbit_array(:,end) = r./R_earth; ground_track = r./R; ground_track_array(:,1:end-1) = ground_track_array(:,2:end); ground_track_array(:,end) = ground_track; for i = 1:N_ground_track x1 = ground_track_array(1,i); y1 = ground_track_array(2,i); ground_track_array(1,i) = x1*cosdphi-y1*sindphi; ground_track_array(2,i) = x1*sindphi+y1*cosdphi; end set(fig_earth,'Cdata',topoc); set(hf,'xdata',orbit_array(1,end),'ydata',orbit_array(2,end),'zdata',orbit_array(3,end)); set(hf_orbit,'xdata',orbit_array(1,:),'ydata',orbit_array(2,:),'zdata',orbit_array(3,:)); set(hf_ground_track,'xdata',ground_track_array(1,:),'ydata',ground_track_array(2,:),'zdata',ground_track_array(3,:)); set(hf_ground_track_end,'xdata',ground_track_array(1,end),'ydata',ground_track_array(2,end),'zdata',ground_track_array(3,end)); set(ht,'string',sprintf('t = %0.2f hours',t/3600)); pause(.01); end end |