Giữa toạ độ, vận tốc và gia tốc có mối quan hệ đạo hàm với nhau. Nhưng hiểu về đạo hàm như thế nào cho đúng? Ta hãy thử quan sát chúng với mô phỏng bằng ngôn ngữ lập trình Matlab.
Xét chuyển động của một vật khối lượng m rơi không vận tốc đầu từ một độ cao nào đó, có tính đến tác động của ma sát trong không khí. Lực ma sát tỉ lệ thuận với vận tốc chuyển động: \vec{F_{ms}}=-k\vec{v}. Quãng đường vật đi được theo thời gian, hay phương trình chuyển động, được diễn tả qua phương trình:
x(t)=\frac{mg}{k}t-\frac{mg}{k}\left(1-\frac{m}{k}e^{-\frac{k}{m}t}\right).\tag{1}
Quy luật này thể hiện trên Matlab qua lệnh:
1 |
Bài toán đặt ra: làm thế nào thu được hàm số của vận tốc và gia tốc trực tiếp từ phương trình chuyển động x(t) theo định nghĩa Matlab (rời rạc) mà không cần sử dụng phép đạo hàm giải tích? Điều này có ý nghĩa rất lớn vì trên thực tế, các thiết bị thu thập toạ độ lưu dữ liệu theo từng con số rời rạc theo thời gian. Trong chuyển động một chiều, vận tốc và gia tốc được định nghĩa như sau:
v=\lim_{\Delta t\to 0} \frac{\Delta y}{\Delta t}=\frac{dy}{dt}\tag{2}
a=\lim_{\Delta t\to 0} \frac{\Delta v}{\Delta t}=\frac{dv}{dt}\tag{3}
Trong thực tế kĩ thuật, máy tính tính toán vận tốc và gia tốc trực tiếp từ chuỗi dữ liệu toạ độ theo các định nghĩa (2-3) một cách trực tiếp. Điều kiện cần là khoảng thời gian giữa hai lần thu thập dữ liệu phải đủ nhỏ.
Trong Matlab giả sử cho hàm số x(t) gồm mảng thời gian t và mảng toạ độ x:
\begin{aligned}t&=[0\quad 1\quad 2\quad 3\quad 4],\\x&=[0\quad 1\quad 4\quad 9\quad 16].\end{aligned}
Để tìm các khoảng dt\approx\Delta t ta dùng lệnh:
1 |
Kết quả sẽ cho ra mảng:
dt=1\quad 1\quad 1\quad 1,
tức các khoảng cách giữa hai số liên tiếp của dãy t. Tương tự để tìm các khoảng dx\approx\Delta x ta dùng lệnh:
1 |
Kết quả sẽ cho ra mảng:
dx=1\quad 3\quad 5\quad 7,
tức các khoảng cách giữa hai số liên tiếp của dãy x. Từ đây ta đã có thể tính vận tốc dựa theo định nghĩa (2):
1 | v = dx./dt; |
Lưu ý rằng độ dài của các dãy dt,dx và v lúc này ít hơn một đơn vị, cho nên mảng biến số thời gian dành cho vận tốc cần giảm bớt một số hạng sau cùng:
1 | tv = t(1:end-1); |
Cuối cùng ta nhận được hàm số v(t_v) cấu tạo từ hai mảng:
\begin{aligned}tv&=[0\quad 1\quad 2\quad 3],\\v&=[1\quad 3\quad 5\quad 7].\end{aligned}
Việc tính gia tốc thực hiện hoàn toàn tương tự. Chương trình dưới đây tính toán vận tốc (lệnh 17-20) và gia tốc (lệnh 23-26) trực tiếp bằng định nghĩa. Dòng lệnh 11 đã chia khoảng thời gian khảo sát 10 giây thành 500 khoảng \Delta t bằng nhau, đủ nhỏ để tiến hành tính vi phân và đạo hàm.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | function vantoc_giatoc clc clear all close all %% INPUT DATA m = 1; k = 1; g = 9.81; t = linspace(0,10,500); %% CALCULATION x = m*g/k*t-m*g/k*(1-m/k*exp(-k/m*t)); % Tinh toan van toc: dx = diff(x); % Vi phan toa do dt = diff(t); % Vi phan thoi gian v = dx./dt; tv = t(1:end-1); % Mang thoi gian danh cho van toc % Tinh toan gia toc: dv = diff(v); % Vi phan van toc dt = diff(tv); % Vi phan thoi gian a = dv./dt; ta = tv(1:end-1); % Mang thoi gian danh cho gia toc %% FIGURE figure('name','Toa do','color','white','numbertitle','off'); plot(t,x,'linewidth',2); xlabel('Thoi gian'); ylabel('Toa do [m]'); figure('name','Van toc','color','white','numbertitle','off'); plot(tv,v,'linewidth',2); xlabel('Thoi gian'); ylabel('Van toc [m/s]'); figure('name','Gia toc','color','white','numbertitle','off'); plot(ta,a,'linewidth',2); xlabel('Thoi gian'); ylabel('Gia toc [m/s^2]'); end |
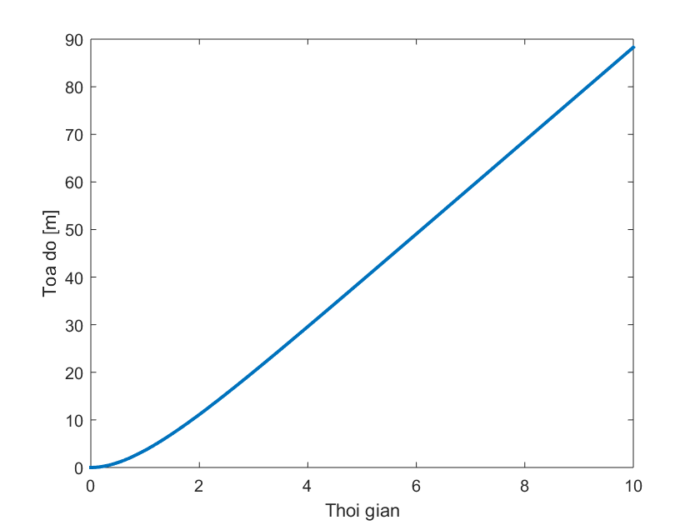
Kết quả tính toán cho ra các đồ thị quãng đường như hình 1. Vật từ từ rời khỏi vị trí ban đầu, tăng tốc nhưng nhanh chóng đạt đến tốc độ ổn định và chuyển động đều.
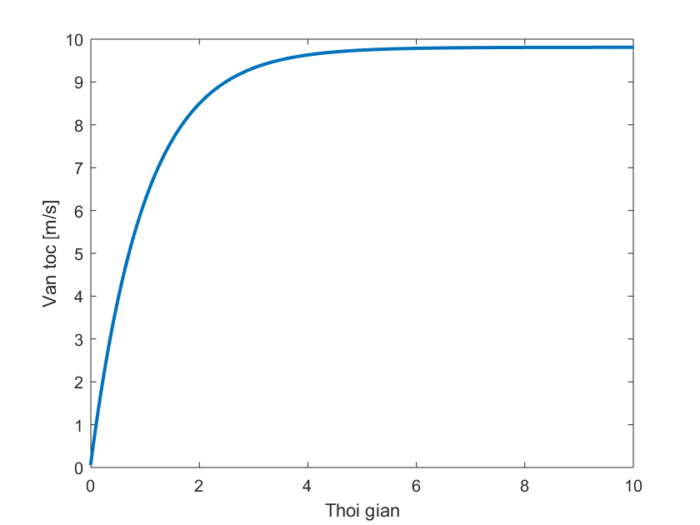
Tính chuyển động đều đó thể hiện rõ ở đồ thị vận tốc hình 2, khi vận tốc ban đầu tăng khá nhanh, nhưng rồi dần ổn định và tiệm cận về một giá trị cụ thể không đổi.
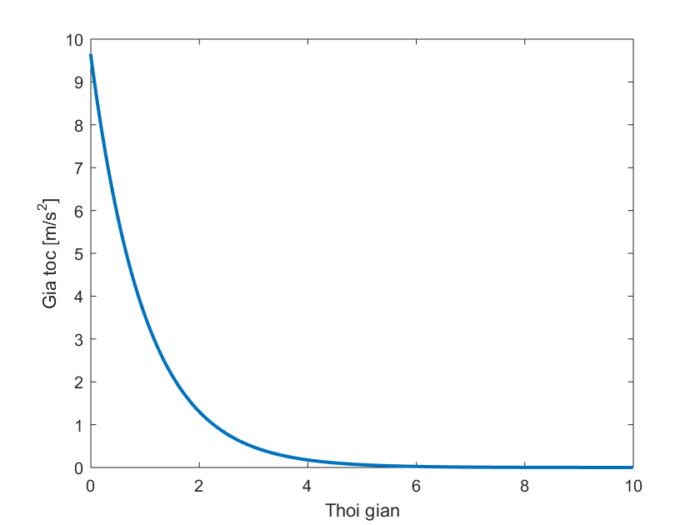
Hình 3 thể hiện quy luật biến đổi của gia tốc. Gia tốc giảm dần từ 9.81 m/s^2 về 0, tức chuyển từ trạng thái chuyển động có gia tốc sang thành chuyển động đều. Sở dĩ có điều đó bởi vì ban đầu vật rơi dưới tác dụng của trọng lực với gia tốc 9.81 m/s^2, nhưng khi vận tốc tăng dần lên thì lực ma sát cũng tăng theo làm giảm gia tốc toàn phần. Khi vận tốc đạt một giá trị nào đó, lực ma sát sẽ trở nên cân bằng với trọng lực khiến vật rơi đều với gia tốc bằng 0.
Thực ra chúng ta đã gán cho vật một phương trình chuyển động x(t) qua hàm giải tích (1) đủ đơn giản để có thể lấy đạo hàm theo phương pháp giải tích:
\begin{aligned}v(t)&=\frac{mg}{k}\left(1-e^{-\frac{k}{m}t}\right),\\a(t)&=ge^{-\frac{k}{m}t}.\end{aligned}
Điều này cho phép ta kiểm chứng lại hoạt động của chương trình máy tính. Thực tế, chương trình máy tính này có thể tính vận tốc và gia tốc với phương trình chuyển động cho trước có dạng bất kì.