Về định luật Stokes và chuyển động trong môi trường ma sát nhớt, chương trình “Thí nghiệm vật lý” có bài “Xác định độ nhớt của chất lỏng“. Chắc hẳn sinh viên nào đã từng thả rơi từng viên bi nhỏ, rồi quan sát chuyển động sẽ thấy sự ảo diệu bay bổng của nó. Ở đây tôi chỉ muốn nhìn nhận từ góc cạnh tính toán kĩ thuật, hay ngôn ngữ Python sẽ làm chuyện ấy như thế nào.
Thí nghiệm
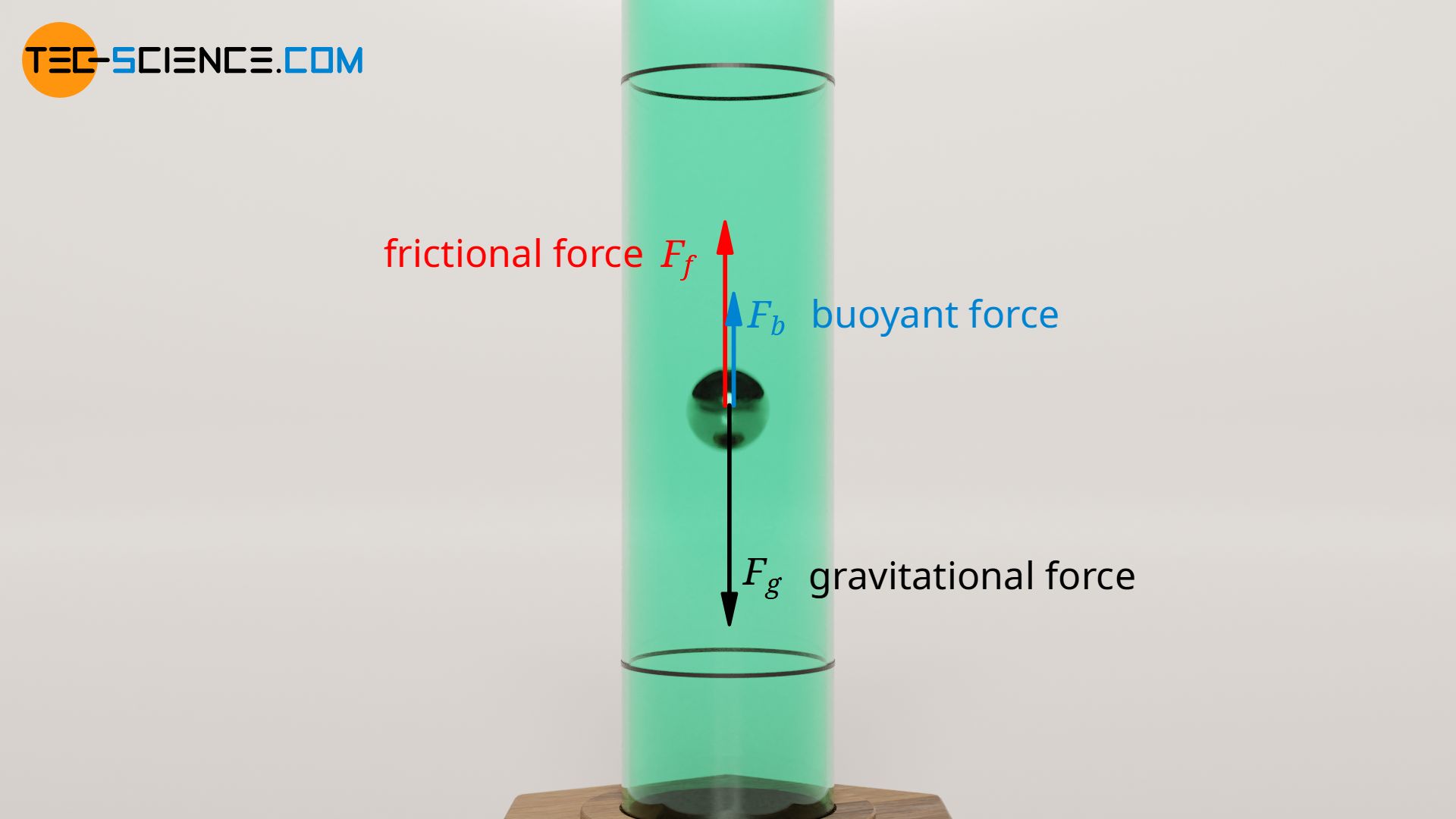
Ta sẽ thả một viên bi sắt hình cầu vào trong một ống nghiệm chứa đầy chất lỏng sệt, ngon ngọt. Vâng, đó là một bình trụ glycerine. Do tính đặc thù này, phòng thí nghiệm đã phải ra khẩu hiệu chống mút trộm, vì bẩn, đồng thời xịt thuốc kiến định kỳ. Đây, ống thuỷ tinh dài như hình dưới:
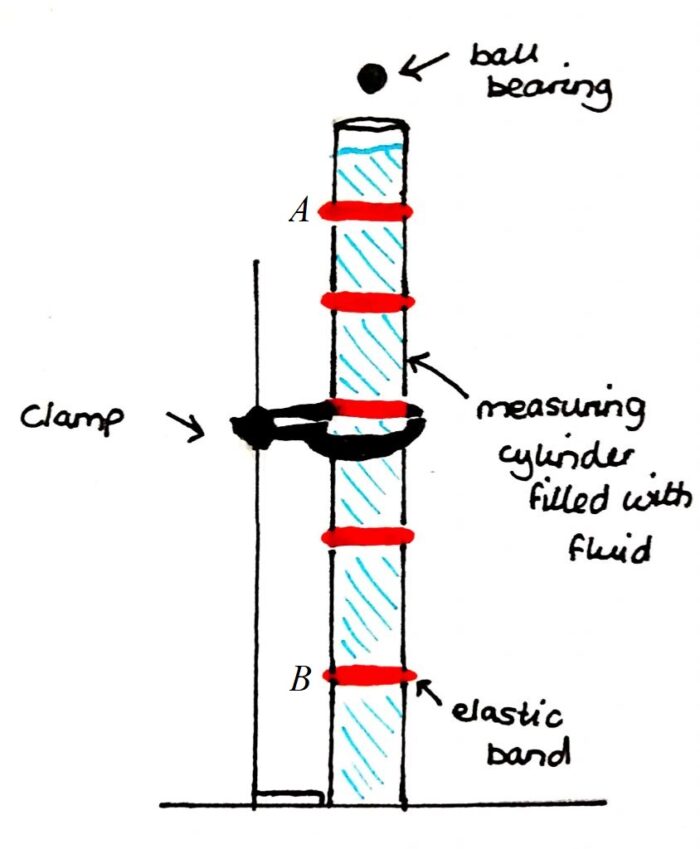
Ban đầu khi thả vào, ta sẽ thấy sự biến đổi tốc độ. Nếu thả nhẹ nhàng từ mặt thoáng, hòn bi sẽ tăng tốc. Nhưng tăng dần đến ngưỡng nhất định thì không tăng nữa, nó rơi đều! Còn nếu thả cao hơn mặt thoáng một đoạn, sau khi rơi tự do trong không khí, hòn bi lao vào glycerine với tốc độ nào đó. Nhưng cuối cùng nó cũng bình ổn về một tốc độ rơi nhất định. Dường như khi thả một chùm hạt cầu sắt như nhau vào, chúng sẽ cùng rơi với một tốc độ như nhau.
Nếu thả rơi những hòn bi sắt kích cỡ khác nhau thì sao? Sau khoảnh khắc tăng giảm tốc nào đó, chúng sẽ lại rơi đều. Nhưng vật nặng hơn sẽ rơi nhanh hơn. Rất khác với định luật Gallile về sự rơi như nhau của mọi vật. Bởi vì quy luật vật lý lúc này sẽ khác.
Định luật Stokes
Để khảo sát cặn kẽ tính chất chuyển động này, ta cần phân tích những thành phần lực tác dụng có mặt trong phương trình định luật II Newton, xét chiều dương trùng với chiều chuyển động xuống dưới:
\[F_g+F_b+F_f=ma.\label{eq:1}\tag{1}\]
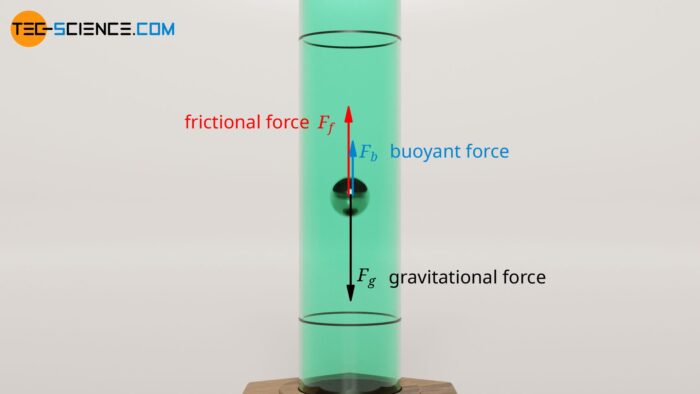
\(F_g=mg=\rho gV\) — trọng lực hướng theo chiều chuyển động. Ở đây \(\rho\) là khối lượng riêng của chất cấu tạo nên vật, \(V=4/3\pi r^3\) — thể tích vật.
\(F_b=-\rho_0gV\) — lực đẩy Archimedes tác dụng theo chiều cản trở chuyển động, với \(\rho_0\) — khối lượng riêng của môi trường chất lỏng, \(V\) — thể tích chất lỏng bị vật choán chỗ, cũng chính là thể tích của vật.
\(F_f = -(k_1v+k_2v^2+\ldots)\) — lực cản tác dụng ngược chiều chuyển động và có độ lớn phụ thuộc vào tốc độ di chuyển.
Các hệ số \(k_1,k_2\ldots\) trong chuỗi số trên phụ thuộc vào hình dạng của vật rơi và tính chất của môi trường. Nếu vật có dạng hình cầu, hệ số \(k_1\) có dạng theo định luật Stokes: \(k_1=6\pi\mu r\), với \(\mu\) — độ nhớt của chất lỏng, còn \(r\) bán kính quả cầu. Khi vật rơi với tốc độ nhỏ, như trong thí nghiệm này, các thành phần bậc cao từ \(v^2\) trở lên có thể bỏ qua. Lực cản có thể biểu diễn đơn giản thành:
\[F_f=-6\pi\mu r\cdot v.\]
Phương trình Newton \(\eqref{eq:1}\) giờ đây viết lại:
\[mg-\rho_0gV -6\pi\mu r\cdot v=ma.\label{eq:2}\tag{2}\]
Giải phương trình
Trước khi đưa ra bất cứ biện luận gì về kết quả tác dụng lực, hãy thử giải phương trình thuần tuý toán học trước. Bạn đọc có thể tin và làm theo, chắc chắn thành công.
Đầu tiên cần viết phương trình động lực \(\eqref{eq:2}\) dưới dạng phương trình vi phân thuần tuý:
\[\frac{d^2y}{dt^2}=\frac{1}{m}\left(mg-\rho_0gV -6\pi\mu r\cdot v\right)\]
diễn tả quy luật của gia tốc. Để giải trên Python, ta biểu diễn thành hệ phương trình vi phân bậc nhất:
\[\begin{aligned}
\frac{dy}{dt}&=v\\
\frac{dv}{dt}&=\frac{1}{m}\left(mg-\rho_0gV -6\pi\mu r\cdot v\right)
\end{aligned}\label{eq:3}\tag{3}\]
Mở môi trường viết Python ra, khai báo các thư viện cần dùng:
import numpy as np import math from scipy.integrate import odeint import plotly.graph_objects as go
Những tham số có mặt trong phương trình động lực học Newton:
g = 9.81 # [m/s^2] rho = 7870 # khoi luong rieng cua vat (Sat) r = 2.0e-3 # ban kinh vat hinh cau rho0 = 1250 # khoi luong rieng chat long mu = 750e-3 # do nhot cua chat long [Pa.s] S = math.pi*r**2 V = 4/3*math.pi*r**3 m = rho*V k1 = 6*math.pi*mu*r # dinh luat Stokes k2 = 0 #0.5*0.4*S*rho0 # cong thuc tinh k2 danh cho vat hinh cau m = rho*V F_Archimedes = rho0*g*V
Hệ phương trình vi phân \(\eqref{eq:3}\) trình bày theo hàm dưới, với \(g,r,\mu,\rho,\rho_0\) là các biến toàn cục:
def model(y,t):
global g,r,mu,rho,rho0
V = 4/3*math.pi*r**3;
m = rho*V;
k1 = 6*math.pi*mu*r # dinh luat Stokes
F_Archimedes = rho0*g*V
F = m*g-F_Archimedes-k1*y[1]-k2*y[1]**2
dy0_dt = y[1]
dy1_dt = F/m
return [dy0_dt,dy1_dt]Tiến hành giải phương trình với điều kiện ban đầu \(y=0\) và \(v=0\):
t = np.linspace(0,0.1,200) # Giải phương trình vi phân solve = odeint(model,y00,t) [y0,y1] = [solve.T[0],solve.T[1]]
Kết quả thu được thể hiện qua đồ thị:
fig = go.Figure()
fig = go.Figure()
fig.add_trace(go.Scatter(x=t,y=y0,mode='lines',name='Toạ độ',
line=dict(color='green',width=1.5)))
fig.update_layout(title='Quãng đường đi được theo thời gian',
xaxis_title='t [s]',
yaxis_title='y [m]')fig = go.Figure()
fig = go.Figure()
fig.add_trace(go.Scatter(x=t,y=y1,mode='lines',name='Vận tốc',
line=dict(color='blue',width=1.5)))
fig.update_layout(title='Vận tốc của vật theo thời gian',
xaxis_title='t [s]',
yaxis_title='v [m/s]')Tốc độ tới hạn
Từ kết quả tính toán trên, ta đã có thể hình dung được toàn cảnh chuyển động của vật rơi trong chất lỏng. Nếu ban đầu thả rơi không vận tốc, vật sẽ chuyển động nhanh dần do trọng lực kéo xuống. Lực nổi Archimedes không thay đổi, do đó trọng lực kết hợp Archimedes về tổng thể là lực kéo xuống không đổi.
Nhưng khi chuyển động càng nhanh, lực cản do môi trường gây ra càng mạnh, tỉ lệ với tốc độ chuyển động. Cho nên khi đạt đến một ngưỡng tốc độ nào đó, lực cản sẽ cân bằng với lực kéo, vật sẽ chuyển động thẳng đều. Có thể đánh giá tốc độ tới hạn này thông qua điều kiện tổng hợp lực bằng không trong phương trình \(\eqref{eq:2}\):
\[(\rho-\rho_0)g\frac{4}{3}\pi r^3-6\pi\mu r\cdot v_T=0.\]
Suy ra tốc độ tới hạn:
\[v_T=\frac{2}{9}\frac{(\rho-\rho_0)g}{\mu}\cdot r^2.\label{eq:4}\tag{4}\]
Ta thấy rằng, nếu giữ nguyên chất liệu hòn bi và chất liệu môi trường thì tốc độ tới hạn chỉ phụ thuộc vào tiết diện ngang của vật rơi. Vật càng lớn, càng chắn nhiều đường dòng chất lỏng lướt qua, thì lực cản càng lớn.
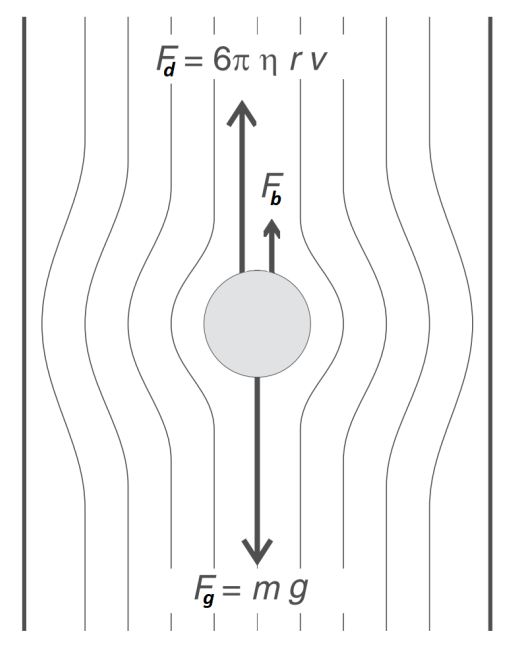
Dễ thấy rằng giá trị của tốc độ tới hạn hoàn toàn không phụ thuộc vào trạng thái thả rơi ban đầu. Dù ta ném/thả vật theo cách gì đi nữa, sau một thời gian vật cũng sẽ rơi ổn định, đều đặn.
Giải lại phương trình \(\eqref{eq:3}\) cho nhiều trường hợp khác nhau của vận tốc ban đầu, tức vận tốc của vật khi bắt đầu chạm mặt thoáng, ta sẽ có được hình ảnh dưới.
v0 = np.linspace(0,0.15,10)
t = np.linspace(0,0.05,200)
fig = go.Figure()
for n in range(len(v0)):
v0 = np.linspace(0,0.15,10)
t = np.linspace(0,0.05,200)
fig = go.Figure()
for n in range(len(v0)):
solve = odeint(model,[0,v0[n]],t)
[y0,y1] = [solve.T[0],solve.T[1]]
fig.add_trace(go.Scatter(x=t,y=y0,mode='lines',name=str(round(v0[n],2))+' m/s',
line=dict(width=1.5)))
fig.update_layout(title='Quãng đường đi được theo thời gian',
xaxis_title='t [s]',
yaxis_title='s [m]',
template = 'plotly_dark')Giai đoạn chuyển động ổn định đặc trưng bằng các đường song song, thể hiện rằng chúng có cùng một tốc độ như nhau.
v0 = np.linspace(0,0.15,10)
v0 = np.linspace(0,0.15,10)
t = np.linspace(0,0.1,200)
fig = go.Figure()
for n in range(len(v0)):
solve = odeint(model,[0,v0[n]],t)
[y0,y1] = [solve.T[0],solve.T[1]]
fig.add_trace(go.Scatter(x=t,y=y1,mode='lines',name='v0 = '+str(round(v0[n],2))+' m/s',
line=dict(width=1.5)))
fig.update_layout(title='Vận tốc của vật theo thời gian',
xaxis_title='t [s]',
yaxis_title='v [m/s]',
template = 'plotly_dark')Đồ thị cho thấy, dù trạng thái ban đầu khác nhau thế nào, sau cùng cũng hội tụ về một tốc độ cố định.
Xác định độ nhớt thực nghiệm
Ý tưởng về đo độ nhớt bằng phương pháp hết sức đơn giản bắt nguồn từ công thức \(\eqref{eq:4}\), khi chuyển độ nhớt \(\mu\) sang vế trái:
\[\mu=\frac{2}{9}\frac{(\rho-\rho_0)g}{v_T}\cdot r^2.\]
Theo đó, chỉ cần cân đo khối lượng riêng \(\rho,\rho_0\), bán kính vật rơi \(r\), xác định được tốc độ rơi ổn định \(v_T\), ta đã có thể tính ra độ nhớt. Để lấy tốc độ \(v_T\), ta đánh dấu hai vạch \(A,B\) như hình đầu tiên và đo thời gian qua đồng hồ bấm giây. Hai vạch chỉ thị phải thuộc đoạn đường rơi ổn định.
Nhưng làm sao biết được từ thời điểm nào vật sẽ bắt đầu rơi ổn định, với \(v_T\) không đổi? Thực nghiệm cho thấy, viên bi càng lớn, càng nặng, thì thời gian thiết lập ổn định càng lâu. Hãy thử tính toán sự thay đổi của vận tốc trong nhiều trường hợp khác nhau của kích thước.
r_array = np.linspace(1e-3,3e-3,10)
t = np.linspace(0,0.1,200)
fig = go.Figure()
for n in range(len(r_array)):
r = r_array[n]
solve = odeint(model,[0,0],t)
[y0,y1] = [solve.T[0],solve.T[1]]
fig.add_trace(go.Scatter(x=t,y=y1,mode='lines',name='r = '+str(round(r*1e3,2))+' mm',
line=dict(width=1.5)))
fig.update_layout(title='Vận tốc của vật theo thời gian',
xaxis_title='t [s]',
yaxis_title='v [m/s]',
template = 'plotly_dark')Quả thực khi bán kính \(r\) càng lớn, thời gian thiết lập sự ổn định càng dài, tốc độ di chuyển càng cao. Nhưng ta cần một biểu diễn khác nhằm đánh giá quãng đường mà mà vật đạt sự ổn định. Hãy xét đồ thị tốc độ phụ thuộc vào quãng đường như hình dưới, với cách xoay trục theo chiều rơi thẳng đứng của vật.
r_array = np.linspace(1e-3,3e-3,10)
rr_array = np.linspace(1e-3,5e-3,10)
t = np.linspace(0,1,200)
fig = go.Figure()
for n in range(len(r_array)):
r = r_array[n]
solve = odeint(model,[0,0],t)
[y0,y1] = [solve.T[0],solve.T[1]]
fig.add_trace(go.Scatter(x=y1,y=-y0,mode='lines',name='r = '+str(round(r*1e3,2))+' mm',
line=dict(width=1.5)))
fig.update_layout(title='Vận tốc theo quãng đường',
xaxis_title='v [m/s]',
yaxis_title='s [m]',
template = 'plotly_dark')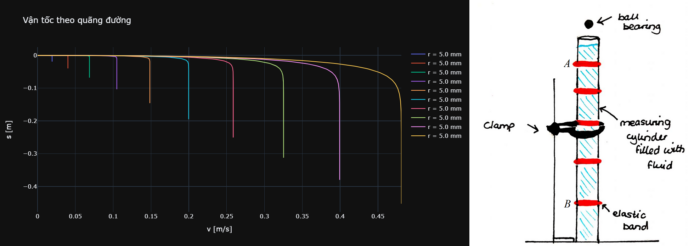
Kết quả tính toán cho thấy, nếu muốn đặt vạch \(A\) – đánh dấu thời điểm vật đã hoàn toàn chuyển động ổn định – cách mặt thoáng 10cm, ta chỉ được phép thả không vận tốc đầu từ mặt thoáng những viên bi có bán kính không quá 3mm. Nếu dùng bi lớn hơn, kéo vạch \(A\) xuống sâu hơn.
Kết luận
Định luật Stokes áp dụng cho vật hình cầu chuyển động chậm, hạn chế dòng chảy rối, tuy mang dáng vẻ đơn giản, nhưng cũng đủ để đánh giá tổng quan đặc tính chuyển động của vật rơi trong chất lỏng. Tổng quát hơn, cần xem xét lý thuyết về dòng chảy Stokes và phương trình Navier – Stokes để có đánh giá đầy đủ hơn.
Tác giả: Trần Hải Cát