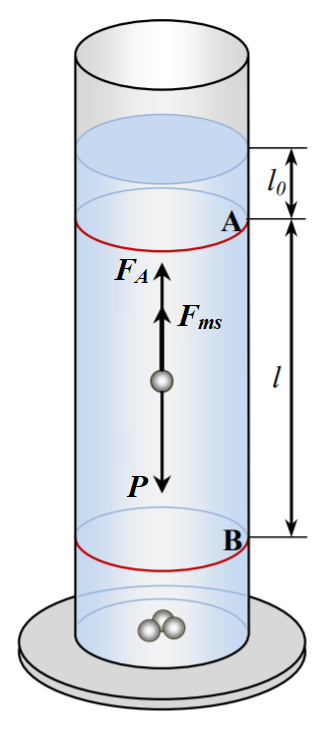
Phát triển từ bài toán “Rơi tự do“, ta tiếp tục khảo sát chuyển động của một vật rơi trong chất lỏng bằng ngôn ngữ Matlab. Trong một bình chứa chất lỏng như hình bên, thả một vật vào bình và quan sát sự rơi của nó theo thời gian.
Vật chịu tác dụng của trọng lực hướng xuống:
\[P=mg=\rho gV,\]
với \(\rho\) – khối lượng riêng của chất cấu tạo nên vật. Lực đẩy Archimedes tác dụng theo chiều ngược lại về phía trên:
\[F_A=\rho_0gV,\]
với \(\rho_0\) – khối lượng riêng của môi trường chất lỏng, \(V\) – thể tích chất lỏng bị vật choán chỗ, cũng chính là thể tích của vật.
Lực ma sát tác dụng ngược chiều chuyển động và có độ lớn phụ thuộc vào vận tốc theo quy luật:
\[F_{ms} = -k_1v-k_2v^2.\]
Các hệ số ma sát \(k_1\) và \(k_2\) phụ thuộc vào hình dạng của vật rơi và tính chất của môi trường. Nếu vật có dạng hình cầu, hệ số \(k_1\) được tính theo định luật Stokes:
\[k_1=6\pi\mu r,\]
với \(r\) là bán kính. Hệ số \(k_2\) tỉ lệ với tiết diện ngang \(S\) của vật, tỉ lệ với khối lượng riêng \(\rho_0\) của môi trường:
\[k_2=\frac{1}{2}cS\rho_0,\]
trong đó \(c\) là tham số phụ thuộc vào hình dạng vật. Tham số này liệt kê vào bảng 1 tương ứng với hình dạng diễn tả trên hình 2.
\[ \text{Bảng 1: Giá trị tham số \(c\) theo hình dạng vật rơi}\\ \begin{array}{c|c|c|c|c|c} \hline \text{Hình đĩa} & \text{Hình cầu} & \text{Bán cầu thuận} & \text{Bán cầu nghịch} & \text{Giọt nước thuận} & \text{Giọt nước nghịch} \\ \hline \text{\(1.11\)} & \text{\(0.4\)} & \text{\(1.33\)} & \text{\(0.55\)} & \text{\(0.045\)} & \text{\(0.1\)}\\ \hline \end{array}\\ \]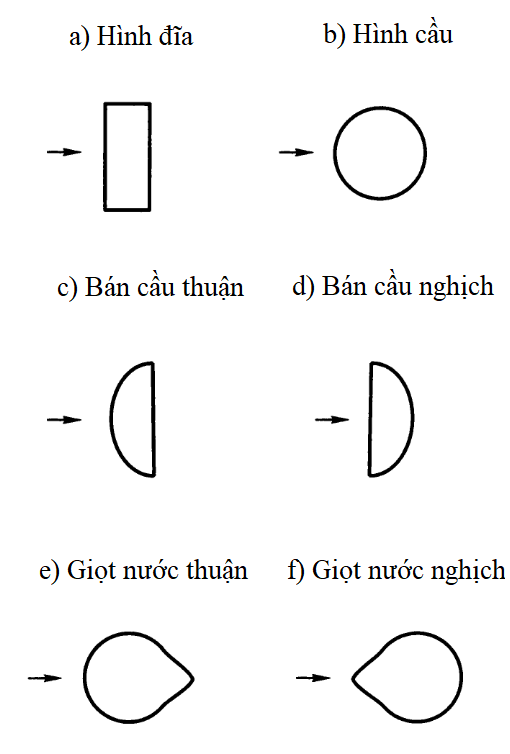
Nhằm thống nhất và đơn giản hoá, chúng ta chọn hình dạng vật thể là hình cầu, tương ứng với \(c=0.4\). Khi ấy:
\[k_2=\frac{1}{2}cS\rho_0=0.2\pi r^2\rho_0.\]
Thể tích vật cũng tính được dễ dàng:
\[V=\frac{4}{3}\pi r^3.\]
Ta thử tiến hành trên Matlab thí nghiệm như sau: Thả một hòn bi sắt đường kính 5 mm vào một bình chứa nước cao 50 cm và quan sát quy luật chuyển động.
Các tham số khai báo qua những dòng lệnh sau:
1 2 3 4 5 6 7 8 9 | %% INPUT DATA h0 = 0.5; % do cao ban dau [m] rho = 7800; % khoi luong rieng cua vat (Sat) R = 2.5e-3; % ban kinh vat hinh cau rho0 = 1000; % khoi luong rieng chat long (Nuoc) mu = 0.9e-3; % do nhot cua chat long [Pa.s] (Nuoc) dt = 0.0005; % [s] |
Từ các tham số do người dùng nhập vào nói trên, chương trình sẽ xử lý sơ bộ qua các lệnh sau để tính khối lượng, tiết diện ngang, thể tích, các hệ số ma sát và thiết lập trạng thái ban đầu:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Phương trình cơ bản của động lực học Newton thể hiện qua lệnh tính gia tốc sau mỗi vòng lặp:
1 2 3 | a = -g+a_Archimedes+F_ms(k1,k2,v)/m; v = v+a*dt; y = y+v*dt+0.5*a*dt.^2; |
Với lực Archimedes và lực ma sát thực thi qua hai chương trình con:
1 2 3 4 5 6 7 8 9 10 |
Video minh hoạ
Code chương trình
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 | function roi_trong_chat_long clc close all clear all global g %% CONSTANTS g = 9.81; % [m/s^2] %% INPUT DATA h0 = 0.5; % do cao ban dau [m] rho = 7800; % khoi luong rieng cua vat (Sat) R = 2.5e-3; % ban kinh vat hinh cau rho0 = 1000; % khoi luong rieng chat long (Nuoc) mu = 0.9e-3; % do nhot cua chat long [Pa.s] (Nuoc) dt = 0.0005; % [s] %% xu ly S = pi*R^2; V = 4/3*pi*R^3; m = rho*V; k1 = 6*pi*mu*R; % dinh luat Stokes k2 = 0.5*0.4*S*rho0; % cong thuc tinh k2 danh cho vat hinh cau x = 0; y = h0; v = 0; a_Archimedes = F_Archimedes(rho0,V)/m; % luc day Archimedes tao gia toc khong doi a = -g+a_Archimedes; t = 0; s = 0; t_array = t; s_array = s; v_array = v; a_array = abs(a); %% FIGURE fig_vatroi = figure('name','Vat roi','color','black','numbertitle','off'); set(gcf,'Units','normalized'); set(gcf,'Position',[0 0.1 0.2 0.8]); graph_quanang = plot(x*100,y*100,'ro','MarkerSize',20,'markerfacecolor','r'); set(gca,'color','k') xlabel('X [cm]'); ylabel('Y [cm]'); dodaivector_g = h0*20; vetrongluc = drawArrow_trongluc('',[0 y*100],[0 y*100-dodaivector_g],'y',false); veluccan = drawArrow_trongluc('',[0 y*100],[0 y*100+a_Archimedes/g*dodaivector_g],'m',false); axis equal axis([-0.15*h0 0.15*h0 -0.2*h0 1.2*h0]*100); fig_quangduong = figure('name','Quang duong','color','white','numbertitle','off'); set(gcf,'Units','normalized'); set(gcf,'Position',[0.2 0.1 0.3 0.38]); graph_quangduong = plot(t_array,s_array,'b','linewidth',2); xlabel('Thoi gian [s]'); ylabel('Quang duong [m]'); fig_vantoc = figure('name','Van toc','color','white','numbertitle','off'); set(gcf,'Units','normalized'); set(gcf,'Position',[0.5 0.1 0.3 0.38]); graph_vantoc = plot(t_array,v_array,'g','linewidth',2); xlabel('Thoi gian [s]'); ylabel('Van toc [m/s]'); fig_giatoc = figure('name','Gia toc','color','white','numbertitle','off'); set(gcf,'Units','normalized'); set(gcf,'Position',[0.2 0.52 0.3 0.38]); graph_giatoc = plot(t_array,a_array,'r','linewidth',2); xlabel('Thoi gian [s]'); ylabel('Gia toc [m/s^2]'); %% CALCULATION while y>0 t = t+dt; t_array = [t_array t]; a = -g+a_Archimedes+F_ms(k1,k2,v)/m; v = v+a*dt; y = y+v*dt+0.5*a*dt.^2; s_array = [s_array h0-y]; v_array = [v_array abs(v)]; a_array = [a_array abs(a)]; figure(fig_vatroi); set(graph_quanang,'xdata',x,'ydata',y*100); drawArrow_trongluc(vetrongluc,[0 y*100],[0 y*100-dodaivector_g],'yellow',true); drawArrow_trongluc(veluccan,[0 y*100],[0 y*100+(a+g)/g*dodaivector_g],'m',true); figure(fig_quangduong); set(graph_quangduong,'xdata',t_array,'ydata',s_array); figure(fig_vantoc); set(graph_vantoc,'xdata',t_array,'ydata',v_array); figure(fig_giatoc); set(graph_giatoc,'xdata',t_array,'ydata',a_array); pause(0.002); end end %% Luc day Archimedes function F = F_Archimedes(rho0,V) global g; F = rho0*g*V; end %% Ham luc ma sat function F = F_ms(k1,k2,v) F = sign(v)*k1*v-sign(v)*k2*v.^2; end %% Ham ve mui ten function hArrow = drawArrow_trongluc(fun,p0,p1,color,draw) % drawArrow(p0,p1) % draw: boolean if nargin == 2 color = 'k'; end % Parameters: W1 = 0.08; % half width of the arrow head, normalized by length of arrow W2 = 0.014; % half width of the arrow shaft L1 = 0.18; % Length of the arrow head, normalized by length of arrow L2 = 0.13; % Length of the arrow inset % Unpack the tail and tip of the arrow x0 = p0(1); y0 = p0(2); x1 = p1(1); y1 = p1(2); % Start by drawing an arrow from 0 to 1 on the x-axis P = [... 0, (1-L2), (1-L1), 1, (1-L1), (1-L2), 0; W2, W2, W1, 0, -W1, -W2, -W2 ]; % Scale,rotate, shift and plot: dx = x1-x0; dy = y1-y0; Length = sqrt(dx*dx + dy*dy); Angle = atan2(-dy,dx); P = Length*P; %Scale P = [cos(Angle), sin(Angle); -sin(Angle), cos(Angle)]*P; %Rotate P = p0(:)*ones(1,7) + P; %Shift % Plot! if draw == 0 hArrow = patch(P(1,:), P(2,:),color); hArrow.EdgeColor = color; else set(fun,'xdata',P(1,:),'ydata',P(2,:),'EdgeColor',color); end end |