Bài 25A: Khảo sát sự phân bố điện trường giữa các điện cực

MỤC ĐÍCH

Bài thí nghiệm này cho phép chúng ta xác định được các đường đẳng thế và các đường sức điện trường, miêu tả sự phân bố điện trường trong không gian giữa các điện cực. Từ đây ta có thể đi đến kết luận rằng, điện trường giữa các điện cực hoàn toàn phụ thuộc vào vào hình dáng và sự bố trí của các điện cực ấy.

MỐI LIÊN HỆ GIỮA CƯỜNG ĐỘ ĐIỆN TRƯỜNG VÀ ĐIỆN THẾ

Cường độ điện trường và điện thế đều là những mặt biểu hiện của một thực thể duy nhất là điện trường.

Với cách biểu diễn qua cường độ điện trường, toàn bộ không gian được lấp đầy bởi trường vector \(\vec{E}\). Tại mỗi vị trí bất kì, điện trường được đặc trưng bởi cường độ và chiều hướng, thông qua độ dài và chiều hướng của vector cường độ điện trường \(\vec{E}\).

Trường vector \(\vec{E}\) cũng có thể hình dung trực quan qua các đường sức điện trường. Với trường tĩnh, các đường sức này đi ra khỏi điện tích dương và đi vào điện tích âm. Tại một điểm bất kì thuộc đường sức, vector \(\vec{E}\) nằm theo phương tiếp tuyến với đường sức và có chiều hướng như đường sức điện trường.

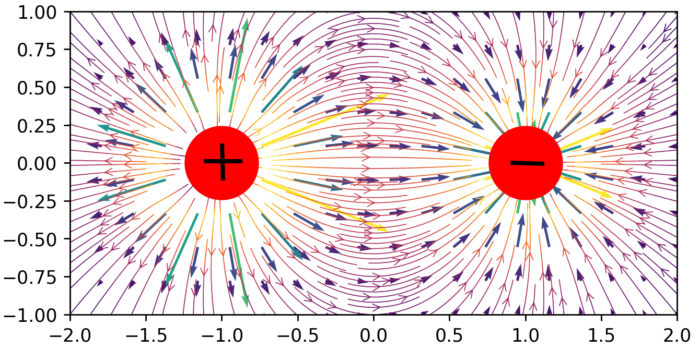
Với cách biểu diễn điện trường theo điện thế, người ta dùng hệ các đường đẳng thế, nối liền các điểm có cùng điện thế: \(V=\mathrm{const}\). Các đường đẳng thế miêu tả điện trường như địa đồ với các đường đồng mức. Theo đó, các đường sức điện trường có xu hướng chảy từ nơi điện thế cao về nơi điện thế thấp. Đặc biệt, đường sức điện trường luôn vuông góc với các đường đẳng thế tại các giao điểm.

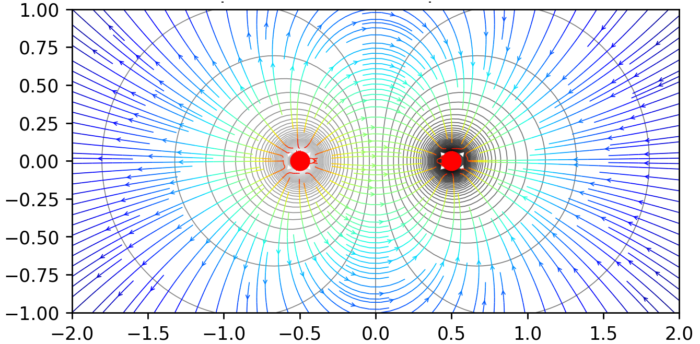
Trong khảo sát thực nghiệm về điện trường, việc xác định vector cường độ điện trường \(\vec{E}\) một cách trực tiếp không thuận lợi về mặt kỹ thuật. Thực tế người ta khảo sát sự phân bố của điện thế, sau đó suy ra vector cường độ điện trường qua mối liên hệ:

\[\vec{E}=-\mathrm{grad}(V).\tag{1}\]

Phương trình trên có ý nghĩa rằng: vector cường độ điện trường \(\vec{E}\) luôn hướng theo chiều suy giảm nhanh nhất của điện thế \(V\) và có độ lớn bằng tốc độ suy giảm của điện thế theo hướng đó.

Nếu chỉ xét cường độ điện trường theo phương \(x\), \(y\) hoặc \(z\), cường độ điện trường theo mỗi phương ấy được tính qua đạo hàm riêng:

\[E_x=-\frac{\partial{V}}{\partial{x}},\quad E_y=-\frac{\partial{V}}{\partial{y}},\quad E_z=-\frac{\partial{V}}{\partial{z}}.\]

NGUYÊN LÝ PHÉP ĐO

Hệ khảo sát của chúng ta cấu thành từ hai điện cực đặt trong một chất lỏng dẫn điện yếu. Cụ thể trong bài thí nghiệm này, ta dùng một bể nước và nhúng hai điện cực vào như hình dưới.

Hai điện cực được nối với hai cực của nguồn điện không đổi có hiệu điện thế \(U_0\). Điện cực nối với cực âm của nguồn gọi là điện cực âm \(K\), hay cathode. Điện cực nối với cực dương của nguồn gọi là điện cực dương \(A\), hay anode. Gốc điện thế có thể chọn tại điện cực âm: \(V_K=0\). Như vậy, điện thế tại điện cực dương \(V_A=U_0\).

Một vôn kế có đầu âm nối liền với điện cực âm \(K\), còn đầu dương là một đầu dò kim loại nhúng vào chất lỏng tại điểm \(P\) bất kì. Trong chất lỏng có các dòng điện chạy từ điện cực dương sang điện cực âm, cũng như có dòng điện chạy từ điểm \(P\) về \(K\), do đó vôn kế sẽ chỉ ra hiệu điện thế giữa \(P\) và gốc điện thế \(K\), cũng chính là điện thế \(V_P\).

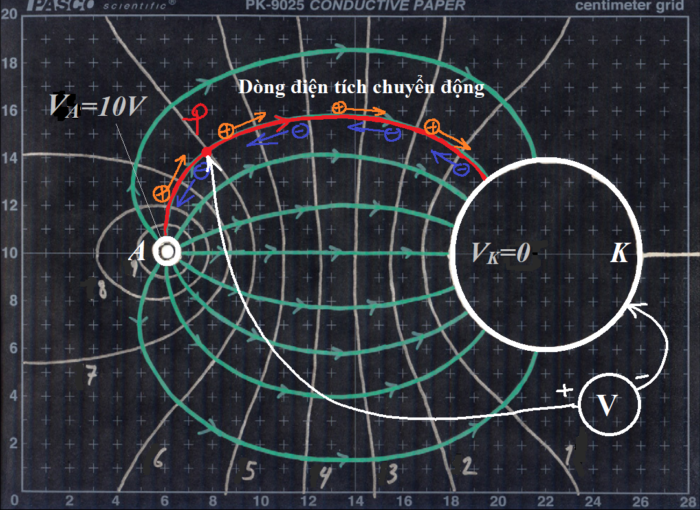
Ta sẽ đi tìm các đường đẳng thế, hay tập hợp các điểm có điện thế \(V_i\) bằng nhau, bằng cách di chuyển đầu dò của volt kế. Tìm được nhiều đường đẳng thế như vậy, ta sẽ có thể suy ra được hệ các đường sức điện trường. Thao tác tính toán xây dựng các đường sức điện trường được miêu tả chi tiết trong phần xử lý dữ liệu.

Lưu ý rằng, nếu không có chất lỏng làm môi trường, sẽ không có dòng điện chạy qua và việc đo điện thế không diễn ra được. Nhưng mặt khác, chúng ta muốn khảo sát điện trường trong chân không chứ không phải điện trường trong môi trường dẫn điện. Một lựa chọn trung dung là sử dụng môi trường chất lỏng dẫn điện yếu. Chỉ khi ấy, các đường sức điện trường chưa bị biến dạng nhiều, và bức tranh điện trường thu được trong thí nghiệm này có thể xem như điện trường trong chân không hoặc không khí.

QUY TRÌNH THÍ NGHIỆM

Sinh viên cần chuẩn bị giấy ô ly có độ chia nhỏ nhất 1mm. Giáo viên sẽ chỉ định loại điện cực, hiệu điện thế \(U_0\) giữa hai điện cực và cách sắp xếp chúng trên bể nước. Sinh viên bố trí lại theo đúng vị trí yêu cầu và vẽ lại hình dạng các điện cực trên giấy ô ly của mình.

Mắc hai điện cực vào nguồn điện không đổi. Bật nguồn và cài đặt hiệu điện thế đến giá trị \(U_0\).

Nối chốt âm của volt kế vào điện cực âm \(K\), còn chốt dương chính là đầu dò để tự do. Để nhận được các đường đẳng thế, ta bắt đầu phép đo theo quy trình sau.

• Dùng đầu dò nhúng vào bể chất lỏng, tìm một điểm có điện thế \(V_1=1\,\mathrm{V}\). Ghi lại vị trí của điểm tương ứng trên giấy ô ly bằng một chấm tròn.
• Dùng đầu dò tìm một điểm khác cũng có điện thế \(V_1=1\,\mathrm{V}\), nằm cách điểm ban đầu không vượt quá \(1\,\mathrm{cm}\).
• Tiếp tục tìm các điểm có cùng mức điện thế như trên chừng nào đầu dò còn chưa vượt ra ngoài phạm vi bể nước.

Tương tự, lặp lại toàn bộ quy trình trên với điện thế \(V_2=2\,\mathrm{V}\), \(V_3=3\,\mathrm{V}\), \(V_n=n<U_0\).

XỬ LÝ DỮ LIỆU

Các đường đẳng thế thu được từ thí nghiệm mới chỉ là các đường rời rạc từ những chấm thực nghiệm. Để bức tranh điện trường rõ nét hơn, ta dùng bút chì vẽ các đường đẳng thế bằng những đường cong trơn, dựa theo các điểm thực nghiệm ở trên. Ghi rõ giá trị điện thế \(V_1,V_2,\ldots\) cho mỗi đường đẳng thế.

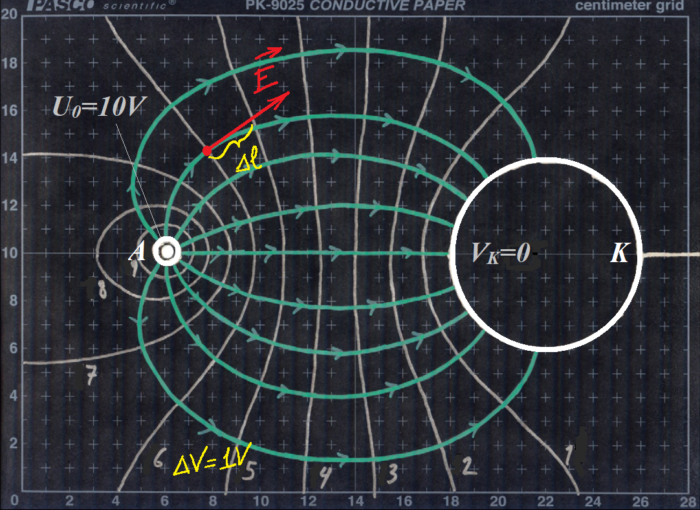
Từ các đường đẳng thế, ta có thể vẽ các đường sức điện trường tương tự như hình 5. Các đường sức điện trường phải vuông góc với các đường đẳng thế tại các giao điểm. Đường sức điện trường kéo dài đến bề mặt các điện cực và vuông góc với bề mặt của điện cực.

Tại mỗi giao điểm giữa đường đẳng thế và đường sức, dựng vector cường độ điện trường theo phương pháp sau:

• Vẽ tiếp tuyến với đường sức tại giao điểm.
• Dùng thước đo khoảng cách \(\Delta l\) từ giao điểm đến đường đẳng thế lân cận có điện thế thấp hơn.
• Tính độ lớn của vector \(\vec{E}\) theo công thức
  \[E=\frac{\Delta V}{\Delta l,}\]
  với \(\Delta V\) là độ suy giảm điện thế từ giao điểm đến đường đẳng thế lân cận.
• Vẽ vector \(\vec{E}\) hướng theo phương tiếp tuyến, có chiều theo hướng suy giảm của điện thế, có độ dài tỉ lệ với độ lớn tính ở bước trên. Cứ 1cm vẽ tương ứng với cường độ điện trường bằng \(100\,\mathrm{V/m}\).