Nguyên lý bất định Heisenberg

Sự xác định và bất định của sóng de-Broglie

Trong bài giảng “Sóng de-Broglie” ta đã đề cập đến sóng phẳng hình sin đại diện cho chùm hạt tự do:

\[\psi_p(x,t)=Ce^{i(\frac{p}{\hbar}x-\frac{E}{\hbar}t)}.\]

Chùm hạt tự do có các hạt chuyển động cùng hướng, cùng vận tốc. Một mặt, tất cả các hạt đều có chung một vector xung lượng \(p\), có hướng trùng với hướng truyền sóng de-Broglie. Ta nói rằng chùm hạt tự do có chung một giá trị xung lượng duy nhất.

Mặt khác, chùm hạt tự do không cho phép chỉ rõ ra một hạt nào. Ta không thể biết được một hạt cụ thể nằm ở đâu trong chùm hạt, vì tất cả bị trộn lẫn đồng nhất với nhau. Bản thân sóng de-Broglie cũng tương ứng với sự phân bố mật độ đều đặn trong không gian, không phụ thuộc vào toạ độ:

\[P=\psi_p^*\psi_p=Ce^{-i(\frac{p}{\hbar}x-\frac{E}{\hbar}t)}Ce^{i(\frac{p}{\hbar}x-\frac{E}{\hbar}t)}=C^2=\mathrm{const}.\]

Ta nói rằng vị trí của hạt hoàn toàn bất định.

Mô hình MỘT hạt tự do

Chùm hạt tự do mang tính bất định trong việc chỉ ra vị trí của hạt, do vậy mô hình một hạt tự do cần có dạng một hàm sóng \(\psi(x,t)\) nào đó, sao cho mật độ của hạt tập trung quanh một điểm nhất định nào đó trong không gian. Hãy khảo sát một sóng hình chuông, đặc trưng cho một hạt đang chuyển động với xung lượng \(p_0\). Tại thời điểm ban đầu \(t=0\) sóng có dạng hàm:

\[\psi(x,0)=Ae^{-x^2/4\sigma_x^2}e^{i(\frac{p_0}{\hbar}x-\frac{E_0}{\hbar}0)}.\label{eq:1}\tag{1}\]

Sóng này có “ruột” giống như một sóng de-Broglie có xung lượng bằng \(p_0\):

\[\psi_p(x,t)=e^{i(\frac{p_0}{\hbar}x-\frac{E_0}{\hbar}t)},\]

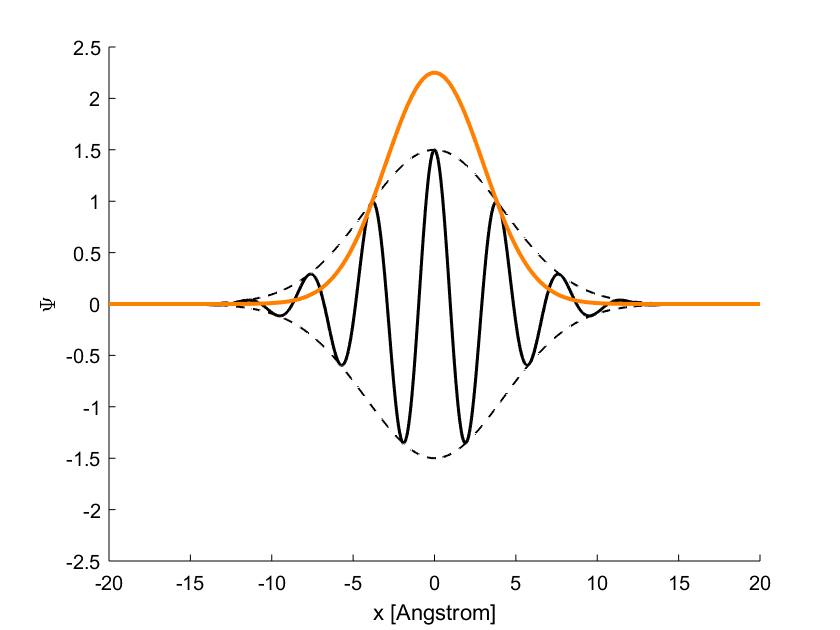
nhưng thực ra không phải sóng de-Broglie, bởi vì biên độ thay đổi theo quy luật \(Ae^{-x^2/4\sigma_x^2}\). Hàm sóng \eqref{eq:1} được diễn tả như hình 2, với \(\sigma_x=3\,\mathrm{A}\). Mật độ của hạt lúc \(t=0\)

\[\psi(x,0)^*\psi(x,0)=Ae^{-x^2/2\sigma_x^2}\]

có dạng của phân bố Gauss với độ lệch chuẩn bằng \(\sigma_x\), diễn tả qua đường màu cam trên hình 2. Như vậy, hàm sóng \eqref{eq:1} diễn tả một “đám mây” hạt mà có đến \(70\,\%\) khối lượng của nó hội tụ quanh vị trí \(x=0\) trong vòng bán kính \(\sigma_x\). Nói cách khác, hạt bây giờ không còn phân tán khắp không gian, mà cô tụ quanh vị trí \(x=0\) với độ bất định bằng \(\sigma_x\).

Phân tích hàm sóng

Phương trình \eqref{eq:1} chỉ miêu tả hình dạng của sóng ban đầu. Rõ ràng khi thời gian trôi đi, sóng sẽ phải di chuyển. Tuy nhiên ta chưa biết được quy luật biến chuyển của sóng như thế nào! Để tìm ra sự di chuyển này, ta tiến hành chuỗi phương án sau:

Bước 1: Phân tích hàm sóng \(\psi(x,0)\) trên hình 2 thành tổng các sóng de-Broglie \(\psi_p(x,0)\).
Bước 2: Sóng de-Broglie \(\psi_p(x,0)\) vừa mới phân tích ra là sóng sin, sau thời gian \(t\) những sóng này trở thành \(\psi_p(x,t)\).
Bước 3: Hàm sóng \(\psi(x,t)\) tại thời điểm \(t\) chính bằng tổng của các sóng de-Broglie \(\psi_p(x,t)\) nói trên.

Thực vậy, hàm sóng bất kì, kể cả sóng hình chuông \(\psi(x,0)\) đang đề cập luôn luôn có thể khai triển ra thành chuỗi Fourier, tức khai triển thành sự chồng chập của những sóng de-Broglie hình sin (khi \(t=0\)):

\[\psi(x,0)=\int\limits_{-\infty}^{\infty}{C(p)e^{i\frac{p}{\hbar}x}\,dp},\label{eq:2}\tag{2}\]

trong đó các hệ số \(C(p)\) phụ thuộc được tính toán theo phép biến đổi Fourier:

\[C(p)=\frac{1}{2\pi\hbar}\int\limits_{-\infty}^{\infty}{e^{-i\frac{p}{\hbar}x}\psi(x,0)\,dx},\label{eq:3}\tag{3}\]

Cận lấy tích phân theo biến xung lượng \(p\) nói trên có thể lấy từ rất nhỏ đến rất lớn. Tuy nhiên, kết quả tính toán hệ số \(C(p)\) ghi lại trên hình 3 cho thấy: để tổng hợp nên sóng hình chuông \eqref{eq:1}, chủ yếu chỉ cần sự góp mặt của những sóng de-Broglie có xung lượng nằm lân cận quanh giá trị \(p_0\).

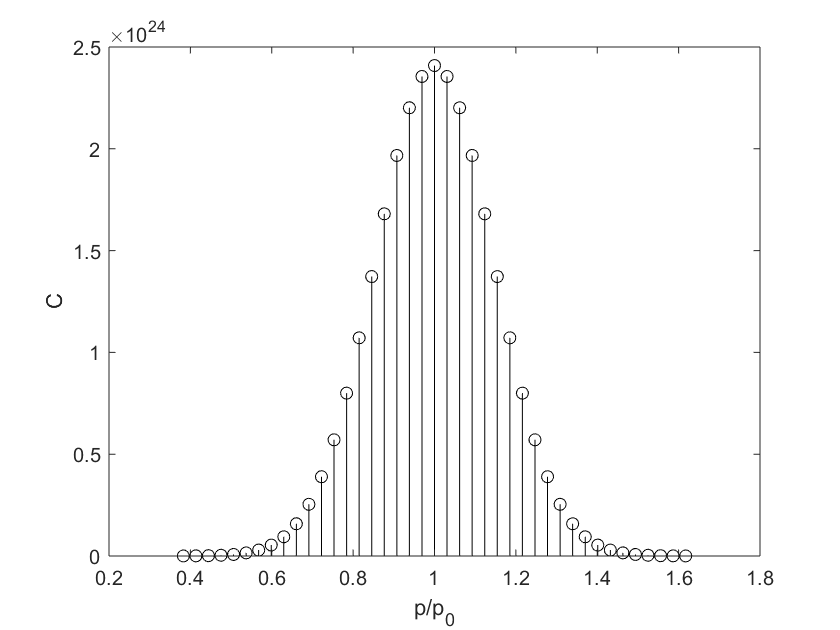
Hình 3: Sự phụ thuộc của hệ số \(C(p)\) vào xung lượng trong khai triển \eqref{eq:2}

Bức tranh tổng hợp trên hình 4 sẽ cho ta lời giải thích cho nhận định trên. Quả thực để “nắn” thành một “chuông sóng” có bước sóng \(\lambda_0=2\pi\hbar/p_0\), đầu tiên ta cần một sóng de-Broglie có xung lượng đúng bằng \(p_0\). Sau đó chồng chập với vài sóng de-Broglie có bước sóng ngắn hơn và dài hơn chỉ một chút, phần trung tâm sẽ được cộng hợp mạnh, còn phần rìa biên sẽ tự tiêu khử nhau do loạn pha. Kết quả ta có được tổ hợp sinh động như hình 4.

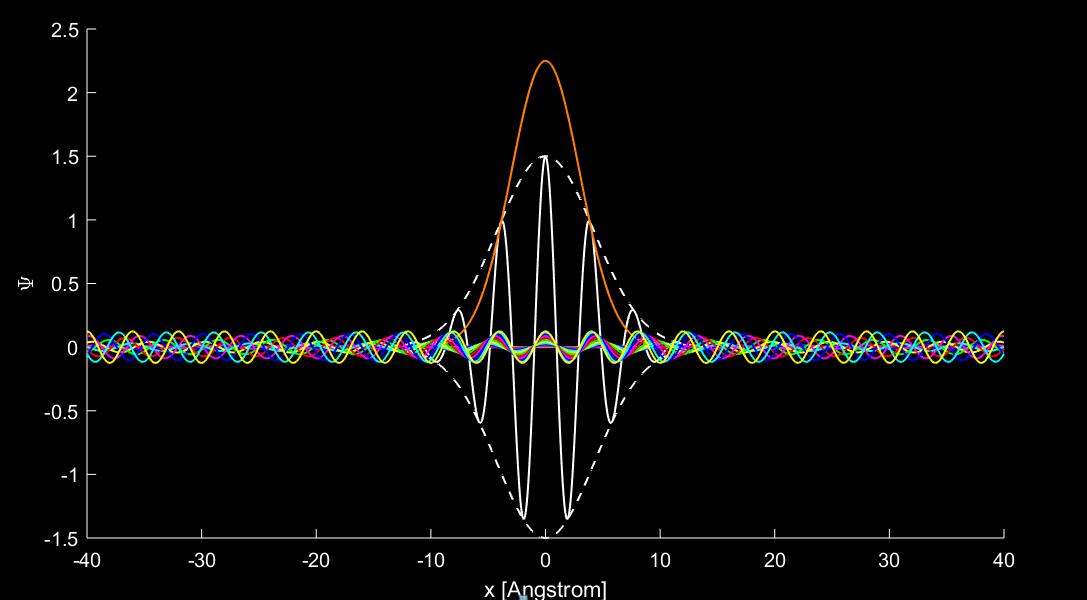
Hình 4: Phân tích hàm sóng ra các thành phần de-Broglie

Trạng thái của hạt tại thời điểm \(t\) bất kì là sự tổng hợp các sóng de-Broglie trở lại:

\[\psi(x,t)=\int\limits_{-\infty}^{\infty}{C(p)e^{i(\frac{p}{\hbar}x-\frac{E}{\hbar}t)}\,dp},\]

với các hệ số \(C(p)\) đã tính được từ phép biến đổi \eqref{eq:3}. Diễn biến quá trình sóng được miêu tả như video dưới. Theo thời gian đám mây hạt di chuyển và cũng bị biến dạng dần, bởi mỗi sóng đơn de-Broglie có tốc độ khác nhau (do xung lượng khác nhau).

Nguyên lý bất định

Từ trên ta thấy, muốn tạo nên một “đám mây hạt” nằm gọn trong bán kính \(\sigma_x=3\,\mathrm{A}\), ta cần sự chồng chập của nhiều sóng de-Broglie cùng lúc, với xung lượng phân tán từ khoảng \(0.8 p_0\) đến \(1.2 p_0\). Bây giờ ta đặt ra bài toán: hãy làm cho đám mây hạt của chúng ta được cô lại gọn gàng hơn, ví dụ với bán kính \(\sigma_x=1.5\,\mathrm{A}\). Đám mây hạt này so với đám mây trước sẽ hẹp hơn, chỉ còn bằng một nửa so với trước (hình 5).

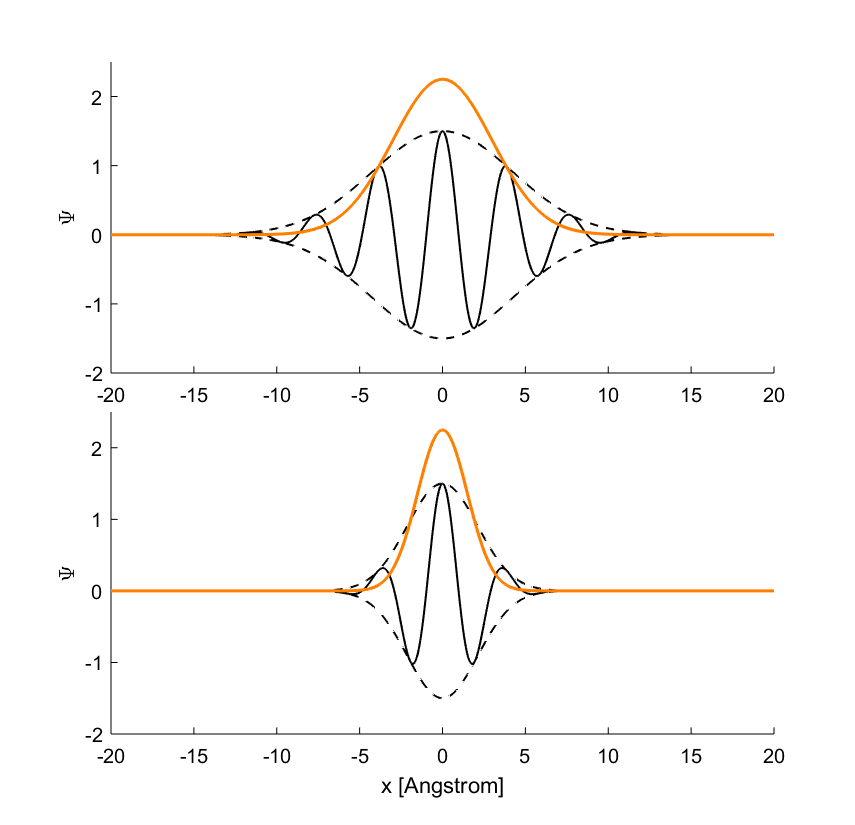
Làm lại phép phân tích bó sóng thành sự chồng chập nhiều sóng de-Broglie như trước, ta có được kết quả phân tích chuỗi Fourier như hình 6, đường màu xanh. Đường màu đỏ tương ứng với phép phân tích bó sóng cũ.

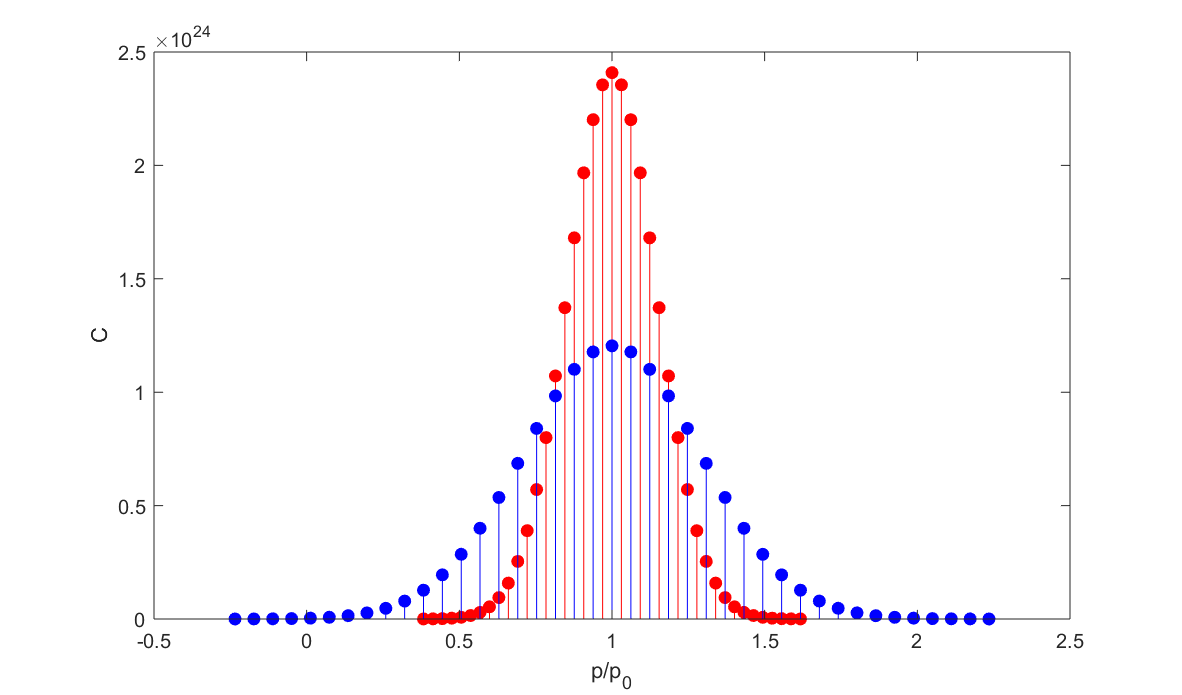
Hình 6: So sánh sự phân tán về xung lượng của hai bó sóng

Hình ảnh cho thấy, khi đám mây hẹp đi 2 lần, ta cần độ phân tán của xung lượng lớn hơn 2 lần. Bó sóng càng hẹp, ta cần dùng càng nhiều sóng de-Broglie để diễn tả nó. Như vậy, khi càng muốn đám mây hạt “sắc nét” hơn trong vị trí, vô tình ta lại làm cho xung lượng càng bị phân tán nhiều hơn. Và đó cũng là nội dung của nguyên lý bất định Heisenberg.

Tính toán chi tiết cho thấy, sự phân bố xung lượng trong phân tích Fourier hình 6 cũng mang dạng hình chuông của phân bố Gauss, với độ lệch chuẩn, hay độ phân tán bằng \(\sigma_p\). Nguyên lý bất định có thể biểu diễn dưới dạng toán học:

\[\sigma_x\sigma_p>\hbar.\]

Bất đẳng thức này nói lên rằng, bán kính của đám mây hạt càng nhỏ, sự phân tán về xung lượng càng lớn. Ngược lại, bán kính đám mây hạt càng lớn, sự phân tán xung lượng sẽ càng nhỏ đi. Đặc biệt, nếu đám mây hạt hoàn toàn “nhoè” đi trong không gian, tức \(\sigma_x\rightarrow\infty\), nó sẽ có xung lượng hoàn toàn xác định \(\sigma_p=0\), tức di chuyển rõ ràng theo một hướng với tốc độ xác định. Điều sau cùng này tương ứng với sóng de-Broglie.

Code chương trình Matlab

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140

function wavepacket_fourier_analys
% Created by Tran Hai Cat
% 2018.03.04
clc;
clear variables
close all

global j h m xmin xmax A

%% CONSTANTS
h = 1.054e-34;
m = 9.1095e-31;
q_element = 1.6e-19;
Angstrom = 1e-10;
j = sqrt(-1);

%% INPUT PARAMETRS
E = 10*q_element;
xmin = -20*Angstrom;
xmax = 70*Angstrom;
x0 = -0*Angstrom; % Initial possition of wave packet
delta_x = 3*Angstrom; % standart deviation (radius of wave packet)
A = 1.5;
Np = 20;

%% DATA PROCESSING
x = linspace(xmin,xmax,1000);
w = E/h; T = 2*pi/w; dt = T/100;
tmax = 100*T;
t = 0;

p0 = sqrt(2*m*E);
[p,C] = packet_analys(E,x,x0,delta_x,Np);

%% FIGURES
figure('name','Analys koefficients of Fourier series',...
'color','white','numbertitle','off')
stem(p/p0,abs(C),'color','k');
xlabel('p/p_0');
ylabel('C');

cstring = 'bcygrm'; % color string
dp = 3*h/delta_x/Np;
figure('name','Synthes wave packet from de Broglie waves',...
'color','black','numbertitle','off')
set(gca,'color','k','xcolor','w','ycolor','w')
hold on
psi = wavepacket_synthes(p,C,x,t);
plot(x/Angstrom,real(psi),'linewidth',1,'color','w');
plot(x/Angstrom,A*exp(-(x-x0).^2/4/delta_x.^2),...
'linestyle','--','linewidth',1,'color','w');
plot(x/Angstrom,-A*exp(-(x-x0).^2/4/delta_x.^2),...
'linestyle','--','linewidth',1,'color','w');
plot(x/Angstrom,psi.*conj(psi),...
'linewidth',1,'color',[1,0.5,0]);
for ip = 1:Np
E = p(ip)*p(ip)/2/m;
psi = C(ip)*de_Broglie(E,p(ip),x,t)*dp;
plot(x/Angstrom,real(psi),...
'linewidth',1,'color',cstring(mod(ip,6)+1));
end
xlabel('x [Angstrom]');
ylabel('\Psi');

figure('name','Wavepaket Free Particle',...
'color','black','numbertitle','off');
hold on
psi = wavepacket_synthes(p,C,x,t);
line_psi = plot(x/Angstrom,real(psi),...
'linewidth',1,'color','w');
line_psi_psi = plot(x/Angstrom,psi.*conj(psi),...
'linewidth',1,'color',[1,0.5,0]);
draw_de_Broglie = zeros(1,Np);
for ip = 1:Np
draw_de_Broglie(ip) = plot(x/Angstrom,real(psi),...
'linewidth',1,'color',cstring(mod(ip,6)+1));
end
axis([xmin/Angstrom xmax/Angstrom -2.0 2.5]);
set(gca,'color','k','xcolor','w','ycolor','w')
xlabel('x [Angstrom]');
ylabel('\Psi');

%% CHANGE OF WAVE FUNCTION OVER TIME
while t<tmax
t = t+dt;
psi = wavepacket_synthes(p,C,x,t);
set(line_psi_psi,'ydata',psi.*conj(psi));
set(line_psi,'ydata',real(psi));
for ip = 1:Np
E = p(ip)*p(ip)/2/m;
psi = C(ip)*de_Broglie(E,p(ip),x,t)*dp;
set(draw_de_Broglie(ip),'ydata',real(psi));
end
pause(0.001);
end

function psi = de_Broglie(E,p,x,t)
%% de Broglie wave (sin wave)
global j h
psi = exp(-j/h*(E.*t-p.*x));

function psi = wavepacket_Gauss(E,x0,delta_x,x)
%% wave packet with Gauss's distribution (normal distribution)
global h m j A
k0 = sqrt(2*m*E)/h;
psi = A*exp(-(x-x0).^2/4/delta_x.^2).*exp(j*k0*(x-x0));

function [p,C] = packet_analys(E,x,x0,delta_x,Np)
%% Calculate koefficients of Fourier's series
global h m
dp = 3*h/delta_x/Np;
p0 = sqrt(2*m*E);
psi0 = wavepacket_Gauss(E,x0,delta_x,x);
p = zeros(1,2*Np+1);
C = zeros(1,2*Np+1);

p(Np+1) = p0;
E0 = p0*p0/2/m;
C(Np+1) = (1/2/pi/h)...
*trapz(x,conj(de_Broglie(E0,p0,x,0)).*psi0);
for ip = 1:Np
p(Np+1-ip) = p0-ip*dp;
E = p(Np+1-ip)*p(Np+1-ip)/2/m;
C(Np+1-ip) = (1/2/pi/h)...
*trapz(x,conj(de_Broglie(E,p(Np+1-ip),x,0)).*psi0);

p(Np+1+ip) = p0+ip*dp;
E = p(Np+1+ip)*p(Np+1+ip)/2/m;
C(Np+1+ip) = (1/2/pi/h)...
*trapz(x,conj(de_Broglie(E,p(Np+1+ip),x,0)).*psi0);
end

function psi = wavepacket_synthes(p,C,x,t)
%% Synthesys initial wave packet from koefficients of Fourier's series
global m
E = p.*p/2/m;
psi = zeros(size(x));
for i = 1:length(x)
psi(i) = trapz(p,C.*de_Broglie(E,p,x(i),t));
end

Bài mới

Nguyên lý bất định Heisenberg

Sự xác định và bất định của sóng de-Broglie

Mô hình MỘT hạt tự do

Phân tích hàm sóng

Nguyên lý bất định

Code chương trình Matlab

Đáng chú ý

Trạng nguyên vật lý mùa 2

Giải nhất thực nghiệm Olympic vật lý quốc gia thuộc về sinh viên ngành cơ điện tử

ADN và cuốn sách cuộc đời

Giải thưởng vật lý danh giá cho nhà khoa học trẻ