Mô-men động lượng

Toán tử mô-men động lượng

Toán tử xung lượng \(\hat{p}=-i\hbar\frac{\partial}{\partial x}\) là hệ quả của lý thuyết de-Broglie về lưỡng tính sóng hạt, gắn liền với sóng de-Broglie. Toán tử động năng \(\hat{T}=-\frac{\hbar}{2m}\frac{\partial^2}{\partial x^2}\) là hệ quả của phương trình Schrodinger. Giữa hai toán tử này lại có mối liên hệ:

\[\hat{T}=\frac{\hat{p}^2}{2m},\]

có hình ảnh rất tương tự với mối quan hệ cổ điển:

\[T=\frac{p^2}{2m}.\]

Điều đó khiến các nhà vật lý nghĩ đến sự mở rộng cho việc định nghĩa các đại lượng mới. Moment động lượng cũng nằm trong số đó. Toán tử moment động lượng được định nghĩa như sau:

\[\hat{M}=[\vec{r}\times\hat{p}]=\left[\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\ x&y&z\\ \hat{p_x}&\hat{p_y}&\hat{p_z}\end{array}\right]\]

với

\[\hat{p_x}=-i\hbar\frac{\partial}{\partial x},\qquad\hat{p_y}=-i\hbar\frac{\partial}{\partial y},\qquad\hat{p_z}=-i\hbar\frac{\partial}{\partial z}.\]

Ta có khai triển theo thành phần:

\[\begin{cases}\hat{M_x}=i\hbar\left(z\frac{\partial}{\partial y}-y\frac{\partial}{\partial z}\right),\\ \hat{M_y}=i\hbar\left(x\frac{\partial}{\partial z}-z\frac{\partial}{\partial x}\right),\\ \hat{M_z}=i\hbar\left(y\frac{\partial}{\partial x}-x\frac{\partial}{\partial y}\right).\end{cases}\]

Toán tử bình phương moment động lượng định nghĩa qua hệ thức:

\[\hat{M^2}=\hat{M_x^2}+\hat{M_y^2}+\hat{M_z^2}=-\hbar\left[\left(z\frac{\partial}{\partial y}-y\frac{\partial}{\partial z}\right)+\left(x\frac{\partial}{\partial z}-z\frac{\partial}{\partial x}\right)+\left(y\frac{\partial}{\partial x}-x\frac{\partial}{\partial y}\right)\right].\]

Trên thực tế, biểu diễn trong hệ toạ độ cầu mang lại nhiều lợi ích thiết thực:

\[\begin{cases}\hat{M_x}=i\hbar\left(\sin\varphi\frac{\partial}{\partial\vartheta}+\mathrm{ctg}\vartheta\cos\varphi\frac{\partial}{\partial\varphi}\right),\\ \hat{M_y}=-i\hbar\left(\cos\varphi\frac{\partial}{\partial\vartheta}-\mathrm{ctg}\vartheta\sin\varphi\frac{\partial}{\partial\varphi}\right),\\ \hat{M_z}=-i\hbar\frac{\partial}{\partial\varphi}.\end{cases}\]

\[\hat{M^2}=-\hbar^2\left[\frac{1}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\left(\sin\vartheta\frac{\partial}{\partial\vartheta}\right)+\frac{1}{\sin^2\vartheta}\frac{\partial^2}{\partial\varphi^2}\right].\]

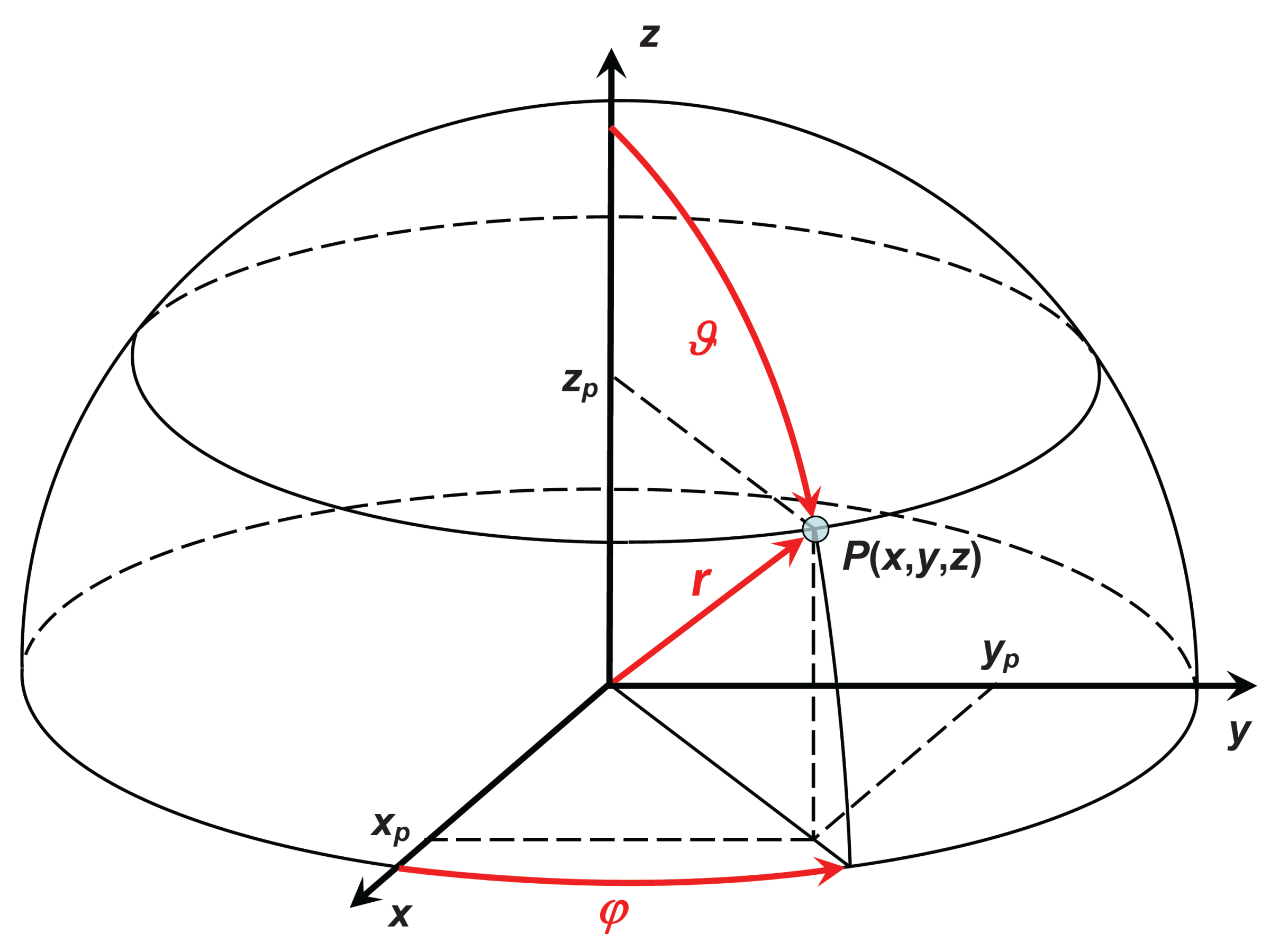
Moment động lượng đối với trục quay

Toán tử \(\hat{M^2}\) nói về moment động lượng toàn phần đối với một điểm làm mốc. Mục này ta tìm hiểu về giá trị của moment động lượng đối với trục quay bất kì nào đó. Không mất tính tổng quát, ta có thể gán trục quay cần tính moment động lượng làm trục \(z\), vì đối với trục này biểu thức của moment động lượng có dạng đơn giản nhất:

\[\hat{M_z}=-i\hbar\frac{\partial}{\partial\varphi}.\]

Ta sẽ đi tìm hàm sóng tương ứng với trạng thái, khi hạt có moment động lượng hoàn toàn xác định, bằng đúng \(M_z\). Theo tính chất của hàm riêng và giá trị riêng:

\[\hat{M_z}\Psi(r,\vartheta,\varphi,t)=M_z\Psi(r,\vartheta,\varphi,t),\]

hay:

\[-i\hbar\frac{\partial}{\partial\varphi}\Psi(r,\vartheta,\varphi,t)=M_z\Psi(r,\vartheta,\varphi,t).\label{eq:1}\tag{1}\]

Phương trình \eqref{eq:1} có nghiệm dễ thấy:

\[\Psi(r,\vartheta,\varphi,t)=\Psi_{r,\vartheta,t}(r,\vartheta,t)e^{i\frac{M_z}{\hbar}\varphi}.\label{eq:2}\tag{2}\]

Biểu thức \(\Psi_{r,\vartheta,t}(r,\vartheta,t)\) ở đây như một hệ số nhân vào, không phụ thuộc vào \(\varphi\). Theo dạng hàm \eqref{eq:2} thu được, đám mây hạt muốn có moment động lượng xác định theo trục \(z\), nó phải quay quanh trục \(z\). Để hiểu rõ, cần đọc bài “Ý nghĩa toán tử quay của kí hiệu \(i\)“.

Nhìn chung khi đám mây hạt quay quanh trục \(z\), nó có thể mang moment động lượng \(M_z\) với giá trị bất kì. Hạt lúc này trông như một con quay, sóng chạy vòng quanh tự giao thoa hỗn loạn. Tuy nhiên, chúng ta lại quan tâm đến những trạng thái dừng, khi năng lượng của hạt có mức xác định. Sóng phải có dạng sao cho khi chạy quanh \(z\), sự giao thoa cho ra một sóng dừng.

Sóng dừng chỉ xuất hiện khi đảm bảo điều kiện:

\[e^{i\frac{M_z}{\hbar}\varphi}=e^{i\frac{M_z}{\hbar}\left(\varphi+m2\pi\right)},\qquad m=0,\pm 1,\pm 2\ldots\]

Điều đó chỉ có được khi moment động lượng \(M_z\) là bội số nguyên của hằng số Planck:

\[M_z=m\hbar.\label{eq:3}\tag{3}\]

Thực vây:

\[e^{i\frac{M_z}{\hbar}\left(\varphi+m2\pi\right)}=e^{im\left(\varphi+m2\pi\right)}=e^{im\varphi+im2\pi}=e^{im\varphi}=e^{i\frac{M_z}{\hbar}\varphi}.\]

Như vậy hạt có moment động lượng hoàn toàn xác định theo trục \(z\), lại vừa có mức năng lượng xác định, phải là một sóng dừng có dạng:

\[\Psi(r,\vartheta,\varphi,t)=\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}\cdot e^{-i\frac{E}{\hbar}t},\qquad m=0,\pm 1,\pm 2\ldots\label{eq:4}\tag{4}\]

Và giá trị của moment động lượng bị lượng tử hoá theo \eqref{eq:3}. Sự lượng tử hoá này có nguyên nhân bản chất do sự giới hạn của góc quay: góc quay chỉ lặp đi lặp lại trong không gian từ \(0\rightarrow 2\pi\). Do đó ta còn gọi đây là sự lượng tử hoá không gian.

Mô hình so sánh với dao động màng rung

Trạng thái dừng có moment động lượng \(M_z=0\) có thể hình dung như một sóng dừng hoàn toàn đối xứng quanh trục \(z\). Lúc này hạt không hề quay, nên nó có moment động lượng bằng không. Khác với thuyết nguyên tử Bohr, theo đó hạt luôn phải quay quanh hạt nhân, nên moment động lượng tối thiểu phải bằng \(1\hbar\). Cơ học lượng tử cho phép trạng thái không có moment động lượng, hạt không cần quay nhưng vẫn không bị rơi vào hạt nhân, đơn giản vì hạt không phải là chất điểm, mà là một đám mây hạt vận động như sóng.

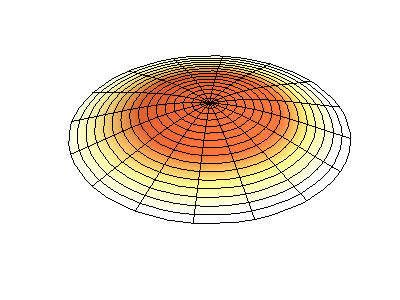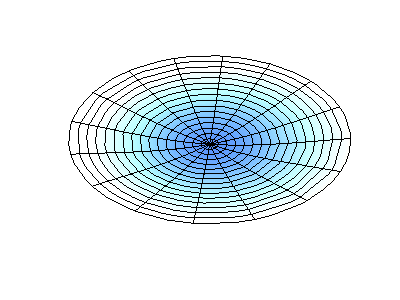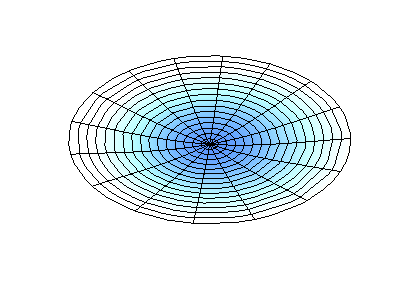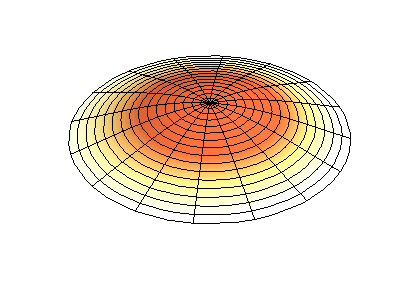
Trạng thái dừng có moment động lượng \(M_z=1\hbar\) có thể hình dung như một sóng dừng với \(2\) bụng sóng.

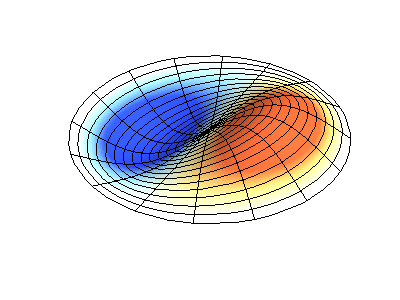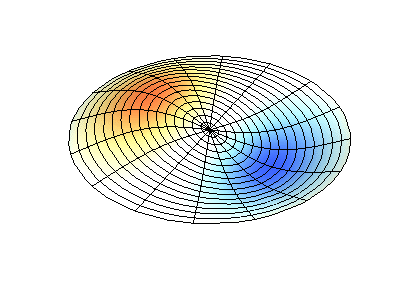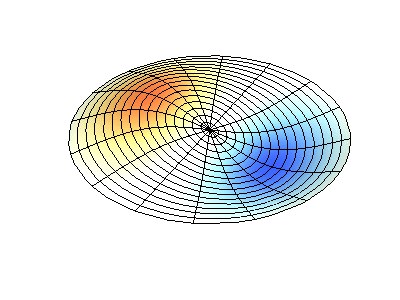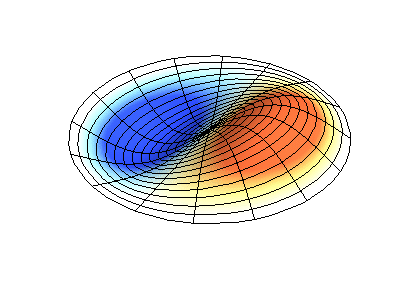
Trạng thái dừng có moment động lượng \(M_z=2\hbar\) có thể hình dung như một sóng dừng với \(4\) bụng sóng.

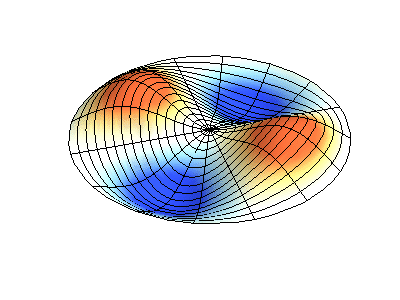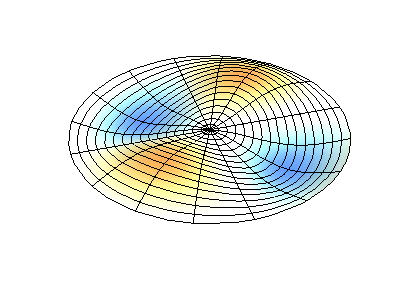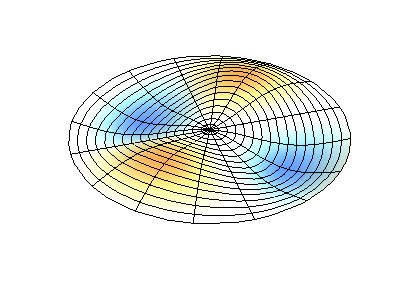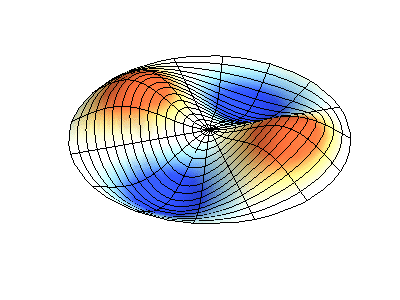
Trạng thái dừng có moment động lượng \(M_z=3\hbar\) có thể hình dung như một sóng dừng với \(6\) bụng sóng.

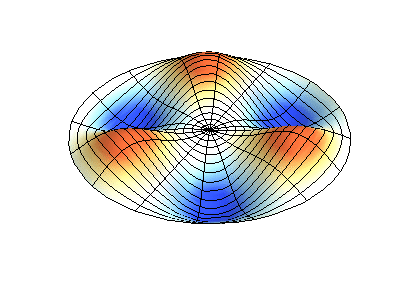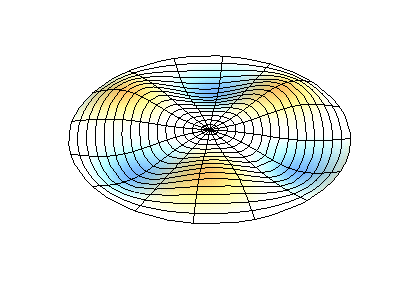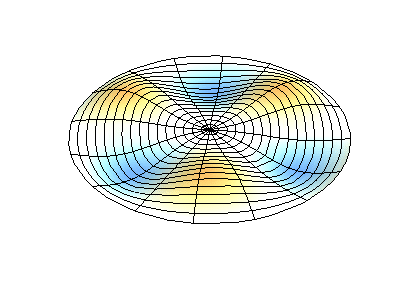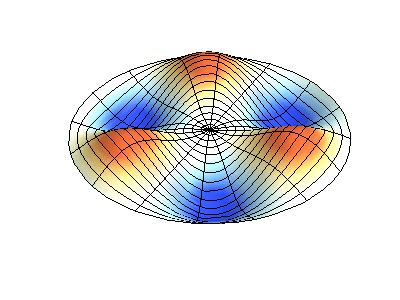
Nguồn hình ảnh minh hoạ màng rung: https://wtt.pauken.org/.

Moment động lượng toàn phần

Khi hạt có moment động lượng \(M_z\) xác định theo trục \(z\), nó phải quay quanh \(z\). Đám mây hạt không thể vừa quay quanh \(z\), vừa quay quanh trục \(x\) cũng như \(y\). Nói cách khác hạt không thể có moment động lượng \(M_x\) và \(M_y\) xác định. Ta không thể xác định đồng thời giá trị các thành phần moment động lượng toàn phần \(M\) theo cả ba trục. Do vậy, hướng của moment động lượng toàn phần hoàn toàn bất định. Trong mục này ta đánh giá chỉ về độ lớn của nó.

Xét một hạt có năng lượng \(E\) hoàn toàn xác định, có moment động lượng \(M_z\) hoàn toàn xác định, với hàm sóng có dạng \eqref{eq:4}:

\[\Psi(r,\vartheta,\varphi,t)=\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}\cdot e^{-i\frac{E}{\hbar}t},\qquad m=0,\pm 1,\pm 2\ldots\]

Nếu hạt có moment động lượng toàn phần hoàn toàn xác định, có giá trị đúng bằng \(M\), hàm sóng phải là hàm riêng của phương trình:

\[\hat{M^2}\Psi(r,\vartheta,\varphi,t)=M^2\Psi(r,\vartheta,\varphi,t),\]

hay:

\[-\hbar^2\left[\frac{1}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\left(\sin\vartheta\frac{\partial}{\partial\vartheta}\right)+\frac{1}{\sin^2\vartheta}\frac{\partial^2}{\partial\varphi^2}\right]\left[\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}\cdot e^{-i\frac{E}{\hbar}t}\right]=M^2\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}\cdot e^{-i\frac{E}{\hbar}t}.\]

Qua chút biến đổi đạo hàm thu được:

\[\frac{1}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\left(\sin\vartheta\frac{\partial}{\partial\vartheta}\right)\left[\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}\right]-\frac{m^2}{\sin^2\vartheta}\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}=-\frac{M^2}{\hbar^2}\Psi_{r,\vartheta}(r,\vartheta)e^{im\varphi}.\]

Bây giờ phương trình không còn chứa đạo hàm theo \(\varphi\) nên có thể lược bớt phần \(e^{im\varphi}\):

\[\frac{1}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\left(\sin\vartheta\frac{\partial}{\partial\vartheta}\right)\Psi_{r,\vartheta}(r,\vartheta)-\frac{m^2}{\sin^2\vartheta}\Psi_{r,\vartheta}(r,\vartheta)=-\frac{M^2}{\hbar^2}\Psi_{r,\vartheta}(r,\vartheta).\]

Phương trình cũng không chứa đạo hàm theo \(r\), nên ta sẽ tìm hàm \(\Psi_{r,\vartheta}(r,\vartheta)\) dưới dạng:

\[\Psi_{r,\vartheta}(r,\vartheta)=R(r)\Theta(\vartheta),\]

theo đó hàm \(R(r)\) chỉ chứa biến \(r\), còn hàm \(\Theta(\vartheta)\) chỉ chứa biến \(\vartheta\). \(R(r)\) có thể là một hàm tuỳ ý, còn \(\Theta(\vartheta)\) là nghiệm của phương trình:

\[\frac{1}{\sin\vartheta}\frac{\partial}{\partial\vartheta}\left(\sin\vartheta\frac{\partial}{\partial\vartheta}\right)\Theta(\vartheta)-\frac{m^2}{\sin^2\vartheta}\Theta(\vartheta)=-\frac{M^2}{\hbar^2}\Theta(\vartheta).\label{eq:5}\tag{5}\]

hay viết dưới dạng thực hành:

\[\Theta”(\vartheta)=-\frac{1}{\tan\vartheta}\Theta'(\vartheta)-\left(\frac{M^2}{\hbar^2}-\frac{m^2}{\sin^2\vartheta}\right)\Theta(\vartheta)\label{eq:6}\tag{6}\]

Giải hàm \(\Theta(\vartheta)\) trên máy tính

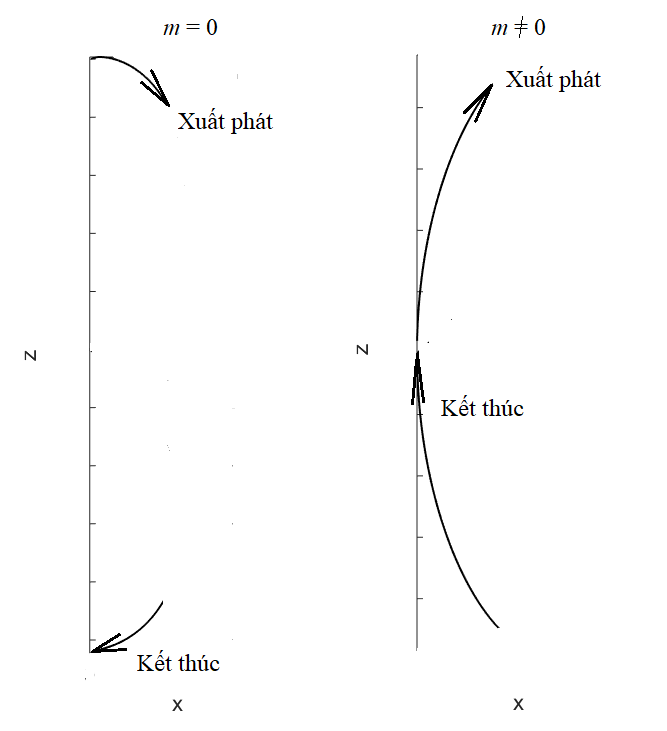
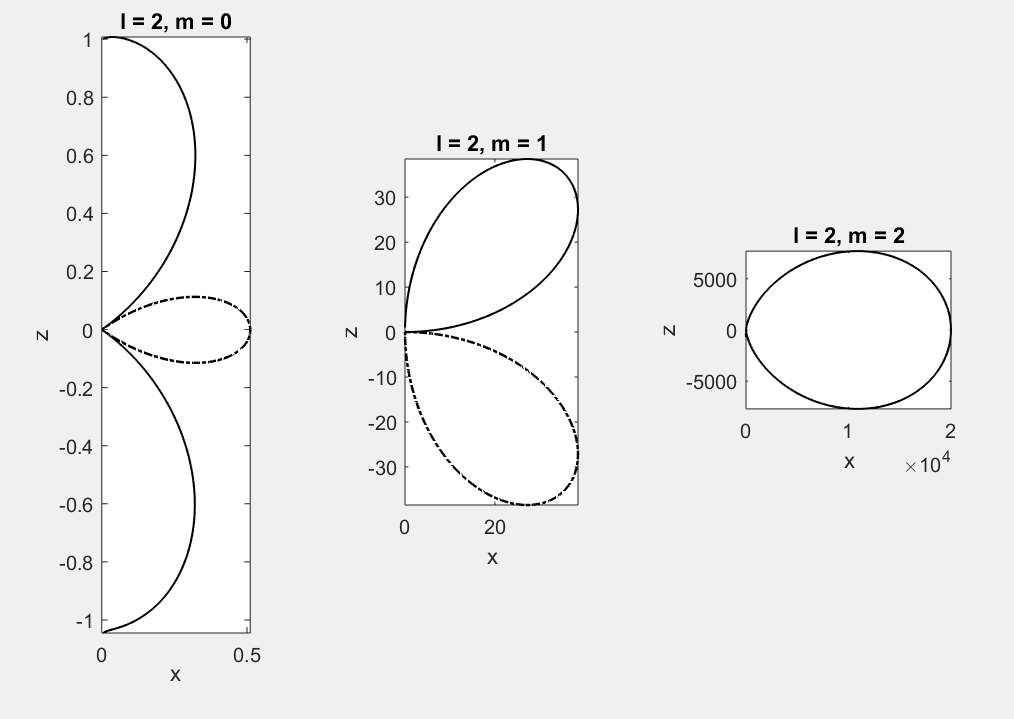
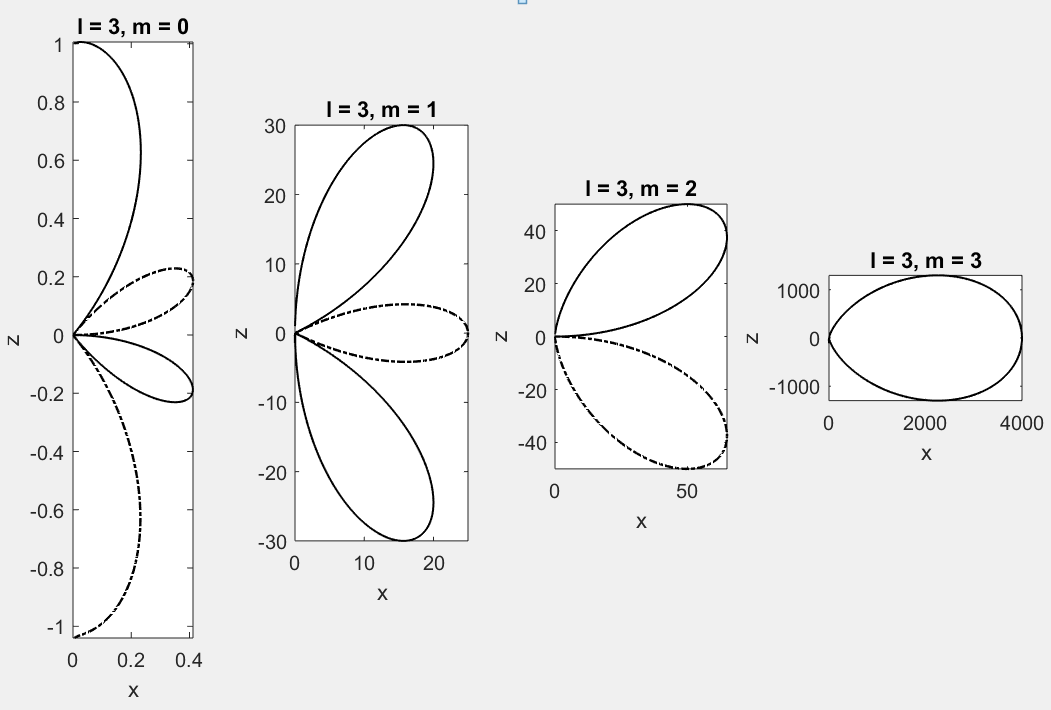
Vì đám mây hạt sẽ quay quanh trục \(z\) nên hàm \(\Theta(\vartheta)\) phải có dạng sao cho trong phép quay đó, sóng phải có dạng cong trơn liên tục theo tự nhiên. Có hai trường hợp xảy ra: \(m=0\) và \(m\neq 0\).

• Nếu \(m=0\), đám mây hạt thực tế không quay và có dạng đồng nhất theo mọi hướng \(\varphi\). Hàm \(\Theta(\vartheta)\) phải bắt đầu tại một điểm nào đó nằm ngay trên trục \(z\) theo hướng nằm ngang và kết thúc tại \(\vartheta=\pi\) cũng theo phương ngang. Điều này tương đương với điều kiện biên \(\Theta'(0)=0\) và \(\Theta'(\pi)=0\).
• Nếu \(m\neq 0\), hàm \(\Theta(\vartheta)\) phải bắt đầu tại gốc toạ độ \(0\) theo hướng thẳng đứng lên trên và kết thúc cũng tại gốc toạ độ theo hướng đâm từ dưới lên. Điều này tương đương với điều kiện biên \(\Theta'(0)\approx+\infty\) và \(\Theta'(\pi)\approx+\infty\).

Bài toán đặt ra cho chúng ta là: Cần chọn giá trị của moment động lượng toàn phần \(M\) bằng bao nhiêu để những điều kiện biên nói trên được thoả mãn? Để trả lời câu hỏi này, cần thử nghiệm giải phương trình \eqref{eq:5} hay \eqref{eq:6} với nhiều giá trị \(M\) khác nhau.

Phương trình \eqref{eq:6} trình bày trên Matlab theo code:

Phép giải tiến hành qua lệnh:

Hoá ra, chỉ tồn tại một vài giá trị rời rạc của moment động lượng toàn phần \(M\) giúp thoả mãn điều kiện biên:

\[M=\hbar\sqrt{l(l+1)},\qquad l=0,1,2,\ldots\]

Hơn nữa, \(l\) phải có giá trị lớn hơn \(m\). Như vậy với mỗi số nguyên \(l\geq 0\) cho trước, chỉ tồn tại những số nguyên:

\[m=-l,(-l+1),\ldots 0,1,\ldots (l-1),l\]

phương trình \eqref{eq:6} mới có nghiệm. Những hình dưới đây thể hiện kết quả tính toán cho hàm \(\Theta(\vartheta)\) với một vài giá trị nhỏ nhất của \(l\) và \(m\). Đường liền nét biểu thị cho giá trị dương của hàm, còn đường nét đứt thể hiện giá trị âm.

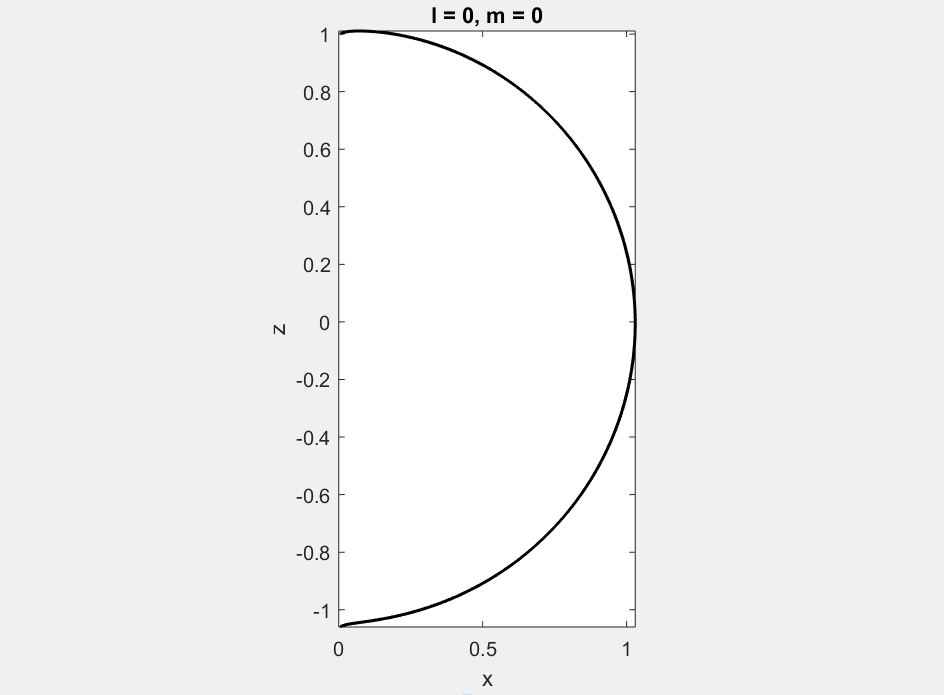
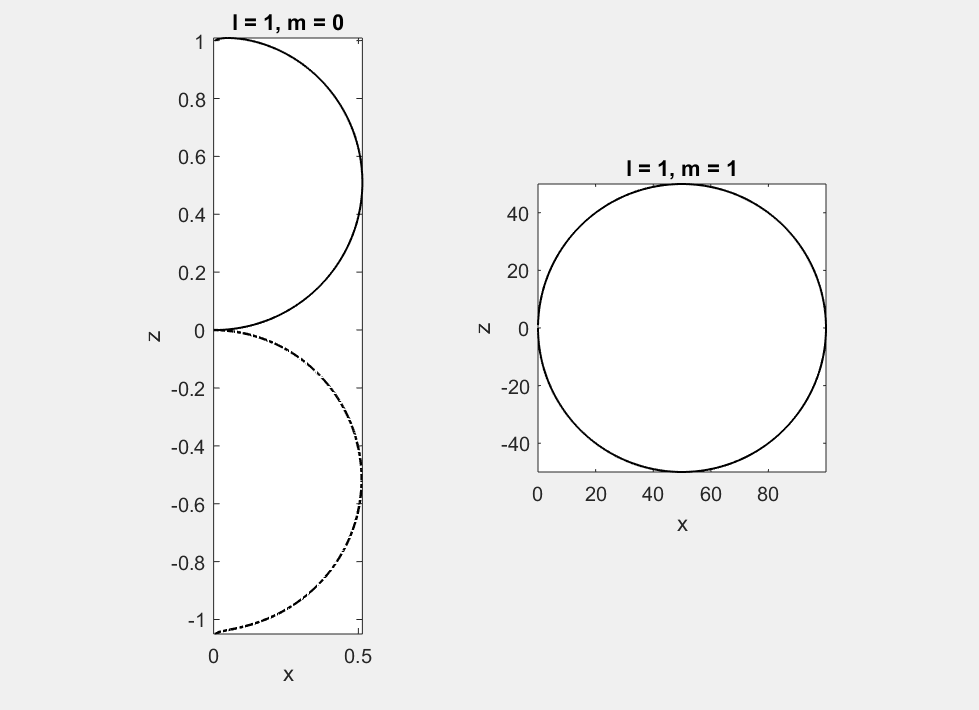
Nhận định chung

Như vậy, hạt có năng lượng \(E\), moment động lượng toàn phần \(M\) cũng như moment động lượng \(M_z\) hoàn toàn xác định sẽ có hàm sóng dạng:

\[\Psi(r,\vartheta,\varphi,t)=R(r)\Theta_{lm}(\vartheta)e^{im\varphi}\cdot e^{-i\frac{E}{\hbar}t}.\]

Trong đó \(m\) là một số nguyên. Hàm \(\Theta_{lm}(\vartheta)\) là nghiệm của phương trình (6) vừa giải ở trên, phụ thuộc vào hai số nguyên \(l\) và \(m\). Còn hàm \(R(r)\) phụ thuộc vào dạng hố thế mà hạt rơi vào.

Moment động lượng toàn phần có giá trị bằng:

\[M=\hbar\sqrt{l(l+1)}.\]

Moment động lượng theo một trục \(z\) nào đó bằng:

\[M_z=m\hbar.\]

Nếu cho trước số nguyên \(l\geq 0\), số nguyên \(m\) sẽ có độ lớn không vượt quá \(l\):

\[m=-l,(-l+1),\ldots 0,1,\ldots (l-1),l.\]

Hàm cầu

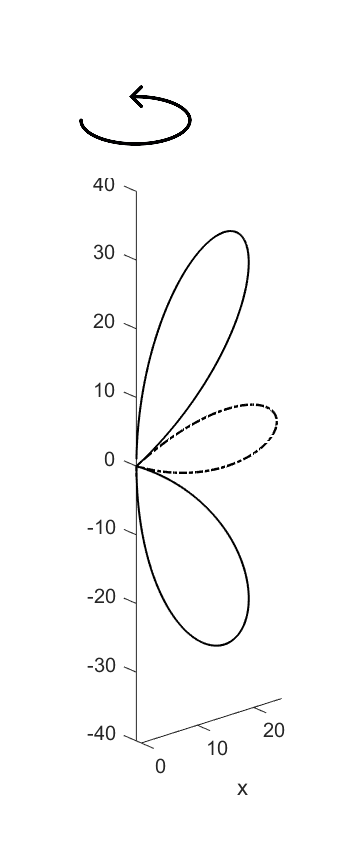
Nhìn chung đám mây hạt quay đều quanh trục \(z\), thể hiện ở thành tố \(e^{im\varphi}\) chứa trong hàm sóng. Để thu được hình ảnh quay của đám mây hạt, ta chỉ cần cho hàm \(\Theta_{lm}(\vartheta)\) vừa tính được ở trên quay quanh trục \(z\), có tính đến bụng sóng và nút sóng do phép quay \(e^{im\varphi}\) tạo ra. Phép quay này tương đương với hàm:

\[Y_{lm}(\vartheta,\varphi)=\Theta_{lm}(\vartheta)e^{im\varphi}\label{eq:7}\tag{7}\]

và ta gọi là hàm cầu. Trong tính toán, hàm cầu thu được qua phần thực của \eqref{eq:7}:

\[Y_{lm}(\vartheta,\varphi)=\Theta_{lm}(\vartheta)\cos(m\varphi).\]

Hàm sóng đầy đủ của hạt có thể trình bày lại theo công thức:

\[\Psi(r,\vartheta,\varphi,t)=R(r)Y_{lm}(\vartheta,\varphi)\cdot e^{-i\frac{E}{\hbar}t}.\]

Video dưới đây trình bày tổng quan kết quả tính toán của hàm cầu với nhiều giá trị \(l,m\) khác nhau. Những vùng màu xanh lá thể hiện phần âm của hàm cầu, tương ứng với pha dao động ngược với những phần còn lại. Thực sự hàm cầu \(Y_{lm}(\vartheta,\varphi)\) thể hiện hình ảnh của vi hạt đang quay quanh một trục khi \(R(r)=1\).

Code chương trình Matlab hoàn chỉnh

• Hàm sóng
• Sóng de Broglie
• Nguyên lý bất định Heisenberg
• Phương trình Schrodinger
• Sóng de-Broglie với rào thế bậc thang
• Bó sóng với rào thế bậc thang
• Sự hình thành trạng thái dừng nguyên tử
• Phương trình dừng Schrodinger
• Giải phương trình Schrodinger bằng phương pháp bắn tên
• Trạng thái dừng trong hố thế vuông
• Dao động tử điều hoà – Phần 1
• Dao động tử điều hoà – Phần 2
• Máy phân tích phổ nhiễu xạ – Toán tử động lượng
• Máy phân tích quang phổ – Toán tử năng lượng
• Đại lượng có giá trị xác định đồng thời
• Mô-men động lượng
• Nguyên tử hidro trong trường hợp đối xứng cầu
• Nguyên tử hidro trường hợp tổng quát
• Đề cương ôn tập Cơ học lượng tử & Vật lý nguyên tử