Máy phân tích quang phổ – Toán tử năng lượng
Máy phân tích quang phổ là thiết bị giúp phân tích quang phổ của chùm sáng phát ra từ một khối vật chất nào đó. Vì mỗi loại nguyên tử và phân tử đều bức xạ những tia có hệ bước sóng đặc trưng, nên qua đánh giá quang phổ, ta có thể thu được thông tin về thành phần nguyên tử và phân tử cấu thành nên khối vật chất đó.
Nguồn gốc của quang phổ hình thành do sự dịch chuyển từ trạng thái dừng có mức năng lượng cao xuống trạng thái dừng có mức năng lượng thấp.
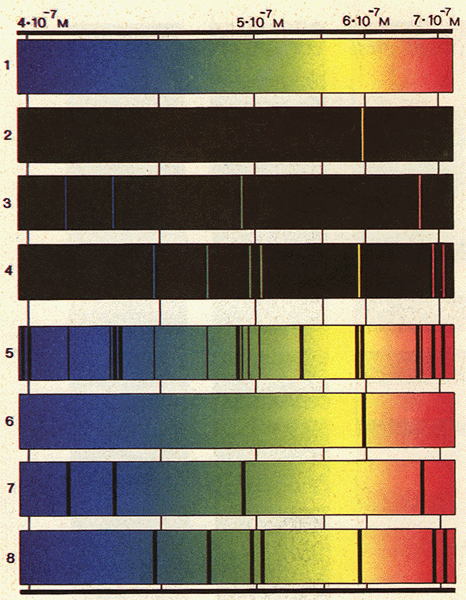
Phép phân tích quang phổ
Lấy mô hình phân tích quang phổ vạch của hidro làm ví dụ. Trước khi làm phép phân tích quang phổ, ta cần chuẩn bị nguồn phát xạ kích thích của nguyên tử hidro, hay còn gọi “đèn hidro”. Đó là một đèn phóng điện giữa hai điện cực, chứa đầy khí hidro. Quá trình phóng điện làm ion hoá hidro phân tử, làm chúng phân tách thành hidro nguyên tử, đồng thời cung cấp năng lượng cho nguyên tử đạt đến những trạng thái kích thích có mức năng lượng cao. Từ những trạng thái kích thích này, hidro nguyên tử sẽ bức xạ photon và biến đổi trạng thái. Sự hấp thụ và bức xạ luôn diễn ra đồng hành.
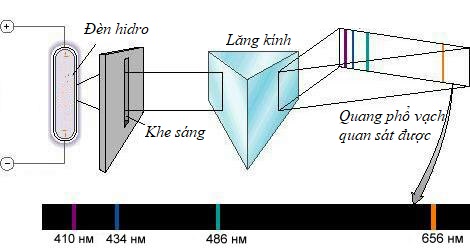
Nếu đèn hidro bị bịt kín, dòng điện sẽ nung khối khí nhốt trong ống đèn thành một khối tương tự như vật đen tuyệt đối. Khi ấy bức xạ bị “cầm tù”, năng lượng của hệ có phổ đặc trưng của vật đen tuyệt đối. Nếu công suất đèn đủ mạnh mà đèn không cháy, có thể hình dung nó giống như một khối nung bức xạ ra phổ liên tục như hình 1.1.
Khi đèn được khoét ô cửa rộng, hoặc để trần với bóng thuỷ tinh, các tia bức xạ sẽ làm nên dòng chảy năng lượng ào ạt thoát ra ngoài. Một quá trình nung nóng, ion hoá, kích thích nguyên tử và bức xạ diễn ra theo dòng chảy này. Theo định luật bảo toàn moment động lượng, các photon phát ra với moment động lượng bằng \(1\hbar\) chỉ xảy ra khi nguyên tử dịch chuyển từ trạng thái dừng này sang trạng thái dừng có moment động lượng ít hơn một đơn vị \(\hbar\). Khi chùm bức xạ ánh sáng này rọi vào quang phổ kế, phổ thu được không phải phổ liên tục của vật đen tuyệt đối, mà là quang phổ vạch rời rạc. Với nguyên tử hidro, đó là dãy Balmer thuộc dải sáng nhìn thấy và nhiều dãy khác.
Như vậy, máy phân tích quang phổ có vai trò tách hàm sóng \(\psi(x,t)\) ra thành sự chồng chập của nhiều trạng thái dừng \(\psi_{E_n}(x,t)\), mỗi trạng thái dừng có mức năng lượng \(E_n\) xác định:
\[\psi(x,t)=\sum_n{C_n\psi_{E_n}(x,t),}\]
Trạng thái dừng \(\psi_{E_n}(x,t)=\Psi_n(x)e^{i(E_n/\hbar)t}\) có hàm biên độ \(\Psi_n(x)\) là nghiệm của phương trình dừng Schrodinger:
\[\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\Psi(x)=E\Psi(x),\label{eq:1}\tag{1}\]
với \(U(x)\) – hàm thế năng. Sau phép tách sóng thành các trạng thái dừng như trên, việc xảy ra sự chuyển hoá từ trạng thái dừng \(\psi_{E_2}(x,t)\) sang trạng thái dừng \(\psi_{E_1}(x,t)\) với năng lượng thấp hơn sẽ kéo theo bức xạ photon với năng lượng:
\[\Delta E=E_2-E_1.\]
Máy phân tích quang phổ tuy thể hiện kết quả dưới dạng phổ năng lượng của photon, nhưng thực chất nó xây dựng bức tranh toàn cảnh về các mức năng lượng làm nên phổ năng lượng photon ấy.
Toán tử năng lượng
Từ phương trình dừng Schrodinger \eqref{eq:1}, các nhà vật lý gọi biểu thức
\[\hat{H}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\label{eq:2}\tag{2}\]
là toán tử năng lượng, hay còn gọi toán tử Hamilton. Toán tử năng lượng này có vai trò tương đương với quang phổ kế. Nếu hệ đang nằm ở trạng thái dừng với mức năng lượng \(E\) xác định:
\[\psi(x,t)=\psi_E(x,t),\]
quang phổ kế sẽ “nhận ra” được mức năng lượng duy nhất này, và năng lượng trung bình \(\langle E\rangle\) cũng phải bằng chính năng lượng duy nhất đó. Thực vậy:
\[\begin{aligned}\langle E\rangle&=\int\limits_{-\infty}^{\infty}{\,\psi_E(x,t)^*\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\psi_E(x,t)dx}\\&=\int\limits_{-\infty}^{\infty}{\,\psi_E(x,t)^*E\psi_E(x,t)dx}\\&=E.\end{aligned}\]
Nếu sóng \(\psi(x,t)\) có dạng bất kì, máy phân tích quang phổ sẽ làm nhiệm vụ phân tích sóng thành tổng phổ:
\[\begin{aligned}\langle E\rangle&=\int\limits_{-\infty}^{\infty}{\,\psi(x,t)^*\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\psi(x,t)dx}\\&=\int\limits_{-\infty}^{\infty}{\,\sum_n{C_n^*\psi_{E_n}(x,t)^*}\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]\sum_n{C_n\psi_{E_n}(x,t)}dx}\\&=\sum_n{\int\limits_{-\infty}^{\infty}{\,C_n^*\psi_{E_n}(x,t)^*\left[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+U(x)\right]C_n\psi_{E_n}(x,t)dx}}\\&=\sum_n{\int\limits_{-\infty}^{\infty}{\,C_n^*\psi_{E_n}(x,t)^*E_nC_n\psi_{E_n}(x,t)dx}}\\&=\sum_n{|C_n|^2E_n}.\end{aligned}\]
Rõ ràng toán tử năng lượng \(\left[-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2}+U(x)\right]\) đang đóng vai trò như một quang phổ kế. Nó phân tích sóng \(\psi(x,t)\) ra các trạng thái dừng \(\psi_E(x,t)\) và đánh giá giá trị năng lượng của mỗi trạng thái dừng đó. Mối liên hệ ấy có thể hình dung qua sơ đồ sau:
- Hàm sóng \(\psi(x,t)\) \(\rightarrow\) Quang phổ kế \(\rightarrow\) Tổng các trạng thái dừng \(\psi_E(x,t)\) \(\rightarrow\) Đánh giá năng lượng qua sự chuyển dịch giữa các trạng thái dừng, biểu hiện bằng quang phổ.
- Hàm sóng \(\psi(x,t)\) \(\rightarrow\) Toán tử năng lượng \(\left[-\dfrac{\hbar^2}{2m}\dfrac{\partial^2}{\partial x^2}+U(x)\right]\) \(\rightarrow\) Tổng các trạng thái dừng \(\psi_E(x,t)\) \(\rightarrow\) Đánh giá năng lượng qua các thành phần trạng thái dừng thu được.
Toán tử động năng
Từ biểu thức \eqref{eq:2} của toán tử năng lượng, ta đưa thêm khái niệm về toán tử động năng:
\[\hat{T}=-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\]
và toán tử thế năng:
\[\hat{U}=U(x).\]
Toán tử năng lượng – Hamilton có thể viết thành:
\[\hat{H}=\hat{T}+\hat{U}.\]
Phương trình Schrodinger cũng có thể trình bày dưới dạng toán tử:
\[\hat{H}\psi(x,t)=E\psi(x,t).\]
- Hàm sóng
- Sóng de Broglie
- Nguyên lý bất định Heisenberg
- Phương trình Schrodinger
- Sóng de-Broglie với rào thế bậc thang
- Bó sóng với rào thế bậc thang
- Sự hình thành trạng thái dừng nguyên tử
- Phương trình dừng Schrodinger
- Giải phương trình Schrodinger bằng phương pháp bắn tên
- Trạng thái dừng trong hố thế vuông
- Dao động tử điều hoà – Phần 1
- Dao động tử điều hoà – Phần 2
- Máy phân tích phổ nhiễu xạ – Toán tử động lượng
- Máy phân tích quang phổ – Toán tử năng lượng
- Đại lượng có giá trị xác định đồng thời
- Mô-men động lượng
- Nguyên tử hidro trong trường hợp đối xứng cầu
- Nguyên tử hidro trường hợp tổng quát
- Đề cương ôn tập Cơ học lượng tử & Vật lý nguyên tử