Máy phân tích phổ nhiễu xạ – Toán tử động lượng

Phép đo động lượng

Trong cơ học lượng tử, trạng thái của hệ vi hạt hoàn toàn được miêu tả qua hàm sóng. Nếu muốn xác định xem động lượng của sóng-hạt có giá trị bằng bao nhiêu, ta cần dùng cách tử nhiễu xạ tinh thể như thí nghiệm Davisson-Germer hình 1.

Cho chùm hạt tự do chiếu vuông góc vào mặt tinh thể nickel, đồng thời bố trí máy thu (detector) ở một góc nào đó. Máy thu cần di chuyển nhằm dò tìm cho được góc cực đại nhiễu xạ \(\vartheta\). Bước sóng de-Broglie có thể tính bằng công thức nhiễu xạ Bragg:

\[\lambda =2d\sin\left(90^{\circ }-{\frac {\vartheta}{2}}\right),\]

trong đó \(d\) – khoảng cách giữa hai nguyên tử liên tiếp trong tinh thể nickel, và suy ra động lượng:

\[p=\frac{2\pi\hbar}{\lambda}.\]

Thí nghiệm này được tiến hành vào năm 1927, củng cố cho lý thuyết Luis de Broglie khi cho rằng, chùm hạt tự do với động lượng \(p\) hoàn toàn tương đương với một sóng sin có dạng:

\[\psi_p(x,t)=e^{i\left(\frac{p}{\hbar}x-\frac{E}{\hbar}t\right)}.\]

Giá trị xung lượng \(p\) sẽ tương ứng với một giá trị \(\vartheta\) trong phép đo, và ngược lại. Nhưng, tình huống sẽ phức tạp hơn nếu ta bắn vào tinh thể không phải chùm hạt đồng nhất, mà là sự hỗn hợp giữa chùm có động lượng \(p_1\) với chùm có động lượng \(p_2\) (hình 2).

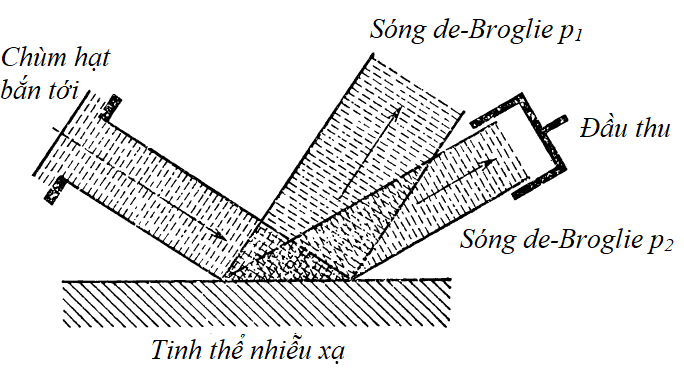
Lúc này, chùm có động lượng \(p_1\) sẽ nhiễu xạ ở góc \(\vartheta_1\), còn chùm kia nhiễu xạ ở góc \(\vartheta_2\), với hai hướng tách bạch rất rõ ràng. Từ đó máy đo có thể xác định được giá trị \(p_1\), \(p_2\) tương ứng. Về bản chất, máy đo đã làm phép phân tích sóng ban đầu thành sự tổng hợp hai sóng de-Broglie:

\[\psi(x,t)=C_1\psi_{p_1}(x,t)+C_2\psi_{p_2}(x,t).\]

Rõ ràng phép đo này không cho ra một giá trị động lượng \(p\) xác định, mà nhiều xung lượng cùng lúc. Vậy nên chỉ có thể nói về động lượng trung bình của sóng \(\psi(x,t)\):

\[\langle p\rangle=|C_1|^2p_1+|C_2|^2p_2,\]

với \(C_1\), \(C_2\) – biên độ của mỗi sóng de-Broglie thành phần.

Máy phân tích phổ nhiễu xạ

Thiết bị cách tử nhiễu xạ tinh thể Davisson-Germer giúp chúng ta phân tích sóng \(\psi(x,t)\) bất kì ra thành sự chồng chập của nhiều sóng de-Broglie:

\[\psi(x,t)=\sum_n{C_n\psi_{p_n}(x,t),}\]

Mỗi sóng de-Broglie \(\psi_{p_n}(x,t)\) đều có giá trị động lượng xác định bằng \(p_n\), cho nên động lượng trung bình của sóng \(\psi(x,t)\) bằng:

\[\langle p\rangle=\sum_n{|C_n|^2p_n}=\sum_n{C_n^*C_n\cdot p_n}.\label{eq:1}\tag{1}\]

Một cách nghệ thuật, nhờ tính trực giao của sóng de-Broglie, ta có thể biểu diễn \eqref{eq:1} dưới dạng đối xứng:

\[\langle p\rangle=\int\limits_{-\infty}^{\infty}{dx\sum_n{C_n^*\psi_{p_n}(x,t)^*}\cdot\sum_n{p_nC_n\psi_{p_n}(x,t)}}.\label{eq:2}\tag{2}\]

Mặt khác, giữa bản thân sóng de-Broglie \(\psi_{p_n}(x,t)\) và động lượng \(p_n\) của nó có mối liên hệ đạo hàm đơn giản:

\[-i\hbar\frac{\partial}{\partial x}\psi_{p_n}(x,t)=-i\hbar\frac{\partial}{\partial x}\left[e^{i\left(\frac{p}{\hbar}x-\frac{E}{\hbar}t\right)}\right]=p_n\psi_{p_n}(x,t).\]

Thế vào \eqref{eq:2}:

\[\langle p\rangle=\int\limits_{-\infty}^{\infty}{dx\sum_n{C_n^*\psi_{p_n}(x,t)^*\cdot\sum_n{-i\hbar\frac{\partial}{\partial x}C_n\psi_{p_n}(x,t)}}}.\]

Hay:

\[\langle p\rangle=\int\limits_{-\infty}^{\infty}{dx\sum_n{C_n^*\psi_{p_n}(x,t)^*}\cdot\left[-i\hbar\frac{\partial}{\partial x}\sum_n{C_n\psi_{p_n}(x,t)}\right]}.\]

Mà:

\[\sum_n{C_n^*\psi_{p_n}(x,t)^*}=\psi(x,t)^*.\]

\[\sum_n{C_n\psi_{p_n}(x,t)}=\psi(x,t).\]

Ta có được công thức tính động lượng trung bình chỉ cần thông qua trạng thái \(\psi(x,t)\):

\[\langle p\rangle=\int\limits_{-\infty}^{\infty}{\,\psi(x,t)^*\left(-i\hbar\frac{\partial}{\partial x}\right)\psi(x,t)dx}.\label{eq:3}\tag{3}\]

Như vậy, thiết bị đo động lượng Davisson-Germer về bản chất là một máy phân tích phổ nhiễu xạ, vừa đóng vai trò như một “máy đạo hàm”, giúp thực hiện phép đạo hàm \(-i\hbar\dfrac{\partial}{\partial x}\) nói trên mà không cần đến toán học. Bản thân đạo hàm trên được gọi là toán tử động lượng:

\[\hat{p}=-i\hbar\frac{\partial}{\partial x}.\]

Công thức \eqref{eq:3} có thể viết thành:

\[\langle p\rangle=\int\limits_{-\infty}^{\infty}{\,\psi(x,t)^*\hat{p}\psi(x,t)dx}.\]

Toán tử động lượng

Toán tử động lượng \(\hat{p}=-i\hbar\dfrac{\partial}{\partial x}\) là môt phương tiện toán học giúp tính toán động lượng trung bình của một sóng \(\psi(x,t)\) bất kì nào đó. Nếu sóng \(\psi(x,t)\) là một chùm hạt tự do đồng nhất de-Broglie:

\[\psi(x,t)=\psi_p(x,t),\]

máy phân tích phổ nhiễu xạ sẽ cho ra đúng một giá trị động lượng duy nhất, và động lượng trung bình \(\bar{p}\) cũng bằng chính động lượng duy nhất đó:

\[\begin{aligned}\langle p\rangle&=\int\limits_{-\infty}^{\infty}{\,\psi_p(x,t)^*\left(-i\hbar\frac{\partial}{\partial x}\right)\psi_p(x,t)dx}\\ &=\int\limits_{-\infty}^{\infty}{\,e^{-i\left(\frac{p}{\hbar}x-\frac{E}{\hbar}t\right)}\left(-i\hbar\frac{\partial}{\partial x}\right)e^{i\left(\frac{p}{\hbar}x-\frac{E}{\hbar}t\right)}dx}\&=p.\end{aligned}\]

Nếu sóng \(\psi(x,t)\) có dạng bất kì, máy phân tích phổ nhiễu xạ sẽ làm nhiệm vụ phân tích sóng thành tổng phổ:

\[\begin{aligned}\langle p\rangle&=\int\limits_{-\infty}^{\infty}{\,\psi(x,t)^*\left(-i\hbar\frac{\partial}{\partial x}\right)\psi(x,t)dx}\\&=\int\limits_{-\infty}^{\infty}{\sum_n{C_n^*\psi_{p_n}(x,t)^*}\left[-i\hbar\frac{\partial}{\partial x}\sum_n{C_n\psi_{p_n}(x,t)}\right]}dx\\&=\sum_n{\int\limits_{-\infty}^{\infty}{\,C_n^*\psi_{p_n}(x,t)^*\left(-i\hbar\frac{\partial}{\partial x}\right)C_n\psi_{p_n}(x,t)dx}}\\&=\sum_n{|C_n|^2p_n}.\end{aligned}\]

Rõ ràng toán tử động lượng \(-i\hbar\dfrac{\partial}{\partial x}\) đang đóng vai trò không khác gì máy phân tích phổ nhiễu xạ, hay thiết bị đo động lượng Davisson-Germer. Nó cũng phân tích sóng \(\psi(x,t)\) ra các thành phần de-Broglie và làm phép đạo hàm. Như vậy, toán tử động lượng có vai trò hoàn toàn tương đương với hoạt động của máy đo động lượng. Mối liên hệ ấy có thể hình dung qua sơ đồ sau:

1. Hàm sóng \(\psi(x,t)\) \(\rightarrow\) Máy phân tích phổ nhiễu xạ \(\rightarrow\) Tổng các sóng de-Broglie \(\rightarrow\) Tính động lượng trung bình \(\bar{p}\) qua góc lệch nhiễu xạ của mỗi sóng de-Broglie thành phần.
2. Hàm sóng \(\psi(x,t)\) \(\rightarrow\) Toán tử động lượng \(-i\hbar\dfrac{\partial}{\partial x}\) \(\rightarrow\) Tổng các sóng de-Broglie \(\rightarrow\) Tính động lượng trung bình \(\bar{p}\) bằng phép đạo hàm lên mỗi thành phần de-Broglie

• Hàm sóng
• Sóng de Broglie
• Nguyên lý bất định Heisenberg
• Phương trình Schrodinger
• Sóng de-Broglie với rào thế bậc thang
• Bó sóng với rào thế bậc thang
• Sự hình thành trạng thái dừng nguyên tử
• Phương trình dừng Schrodinger
• Giải phương trình Schrodinger bằng phương pháp bắn tên
• Trạng thái dừng trong hố thế vuông
• Dao động tử điều hoà – Phần 1
• Dao động tử điều hoà – Phần 2
• Máy phân tích phổ nhiễu xạ – Toán tử động lượng
• Máy phân tích quang phổ – Toán tử năng lượng
• Đại lượng có giá trị xác định đồng thời
• Mô-men động lượng
• Nguyên tử hidro trong trường hợp đối xứng cầu
• Nguyên tử hidro trường hợp tổng quát
• Đề cương ôn tập Cơ học lượng tử & Vật lý nguyên tử