Hàm sóng

Sóng là quá trình lan truyền xung. Một sóng phẳng lan truyền theo chiều dương của trục \(x\) và không bị biến dạng theo thời gian được miêu tả qua hàm sóng có dạng:

\[\psi(x,t)=\psi(x-vt),\label{eq:1}\tag{1}\]

trong đó \(v\) – tốc độ truyền sóng. Tại thời điểm \(t=0\), sóng có dạng hàm \(\psi=\psi(x,0)\). Khi thời gian trôi qua, tại thời điểm \(t\) sau mốc \(t=0\) hàm sóng vẫn giữ nguyên hình dạng \(\psi(x,0)\), nhưng bị kéo sang phải một đoạn đường bằng \(vt\), trở thành dạng \(\eqref{eq:1}\).

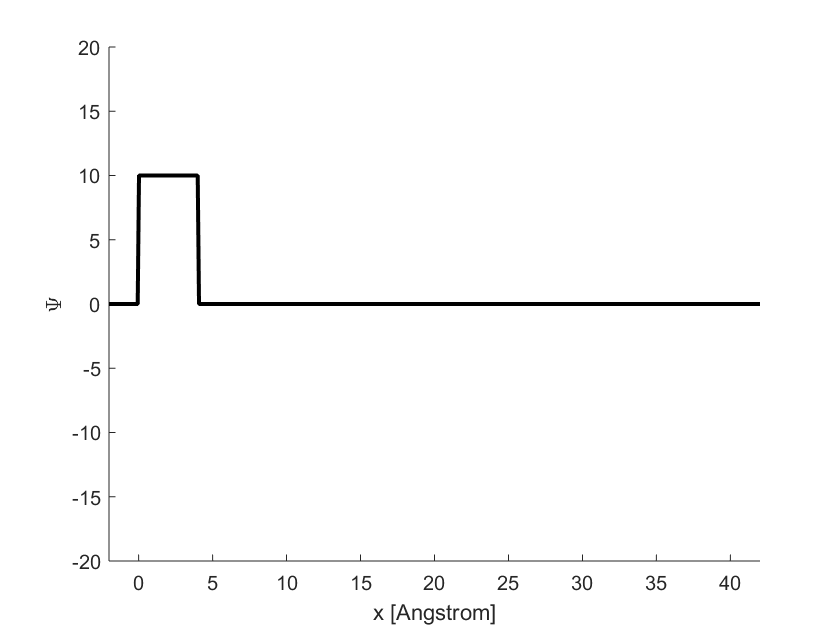
Để cho dễ hình dung, ta hãy lấy ví dụ về một sóng có hình dạng đơn giản, sóng vuông, có hình dạng tại thời điểm ban đầu \(t=0\) là một xung hình vuông có chiều cao \(C=10\) và độ dài \(a=4\cdot 10^{-10}\,\mathrm{m}\):

\[\psi(x,0)=\begin{cases}C&\mathrm{khi}\ x\in(0,a)\\0&\mathrm{khi}\ x\notin(0,a)\end{cases}\label{eq:2}\tag{2}\]

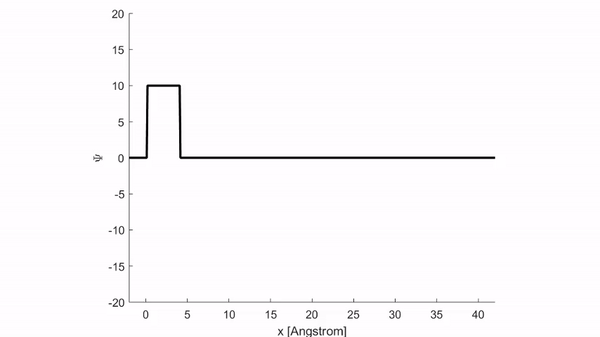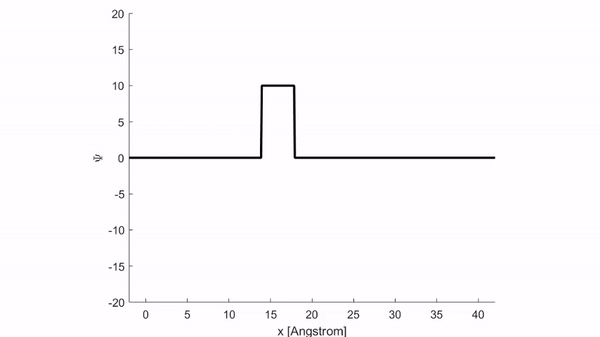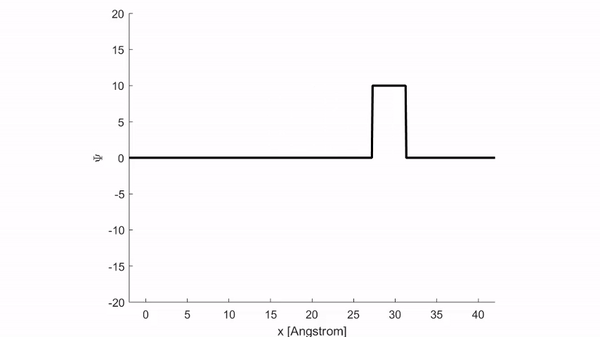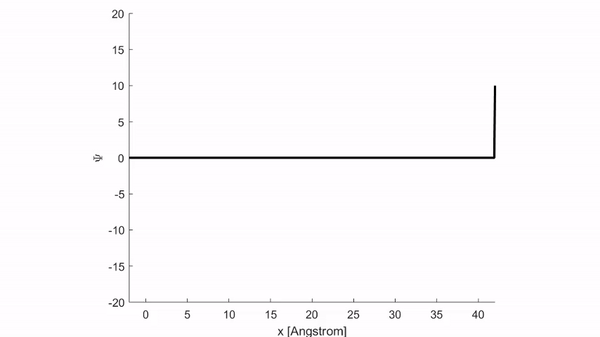
Xung vuông \(\eqref{eq:2}\) có hình dạng và vị trí ban đầu như miêu tả trên hình 1.

Muốn cho xung vuông \(\eqref{eq:2}\) di chuyển sang phải theo chiều dương của trục \(x\) với vận tốc \(v\), ta thay biến \(x\) trong \(\eqref{eq:2}\) thành \(x-vt\):

\[\psi(x,t)=\begin{cases}C&\mathrm{khi}\ (x-vt)\in(0,a)\\0&\mathrm{khi}\ (x-vt)\notin(0,a)\end{cases}\label{eq:3}\tag{3}\]

Khi ấy phương trình \(\eqref{eq:3}\) đã thực sự làm một hàm sóng. Trong Matlab, hàm sóng \(\eqref{eq:3}\) có thể diễn tả qua các dòng lệnh dưới:

1
2
3
4
5
6
7
8
9
10
11
12

function psi = square_wave(x)
%% square wave
global v t
C = 10;
a = 4e-10;
lenx = length(x);
psi = zeros(1,lenx);
for i = 1:lenx
if ((x(i)-v*t)>0) && ((x(i)-v*t)<a)
psi(i) = C;
end
end

Đây là kết quả mô phỏng sự lan truyền sóng vuông khi sử dụng code chương trình đầy đủ bên dưới:

Tương tự ta cũng có thể mô phỏng sự lan truyền của xung tam giác có dạng hàm số:

\[\psi(x,0)=\begin{cases}kx&\mathrm{khi}\ x\in(0,a)\\0&\mathrm{khi}\ x\notin(0,a)\end{cases}\label{eq:4}\tag{4}\]

bằng cách thay \(x\) trong \(\eqref{eq:4}\) thành \(x-vt\):

\[\psi(x,t)=\begin{cases}k(x-vt)&\mathrm{khi}\ (x-vt)\in(0,a)\\0&\mathrm{khi}\ (x-vt)\notin(0,a)\end{cases}\label{eq:5}\tag{5}\]

Trong Matlab, hàm sóng \(\eqref{eq:5}\) có thể viết thành lệnh:

1
2
3
4
5
6
7
8
9
10
11
12
13

function psi = triangle_wave(x)
%% triangle wave
global v t
C = 10;
a = 4e-10;
lenx = length(x);
psi = zeros(1,lenx);
k = C/a;
for i = 1:lenx
if ((x(i)-v*t)>0) && ((x(i)-v*t)<4e-10)
psi(i) = k*(x(i)-v*t);
end
end

Một trường hợp hết sức đặc biệt, thậm chí có vai trò quan trọng trong bộ môn cơ học lượng tử, cần nhắc đến là sóng sin, hay sự lan truyền dao động điều hoà:

\[\psi(x,t)=C\cdot\cos[k(x-vt)]=C\cdot\cos(kx-\omega t),\label{eq:6}\tag{6}\]

trong đó \(k\) và \(\omega\) liên hệ với nhau qua vật tốc \(v=\omega/k\). Ở đây \(k\) được gọi là số sóng, còn \(\omega\) là tần số góc, hay đơn giản là tần số. Số sóng thể hiện “độ giãn” của sóng trong không gian, còn tần số thể hiện “nhịp độ” của sóng theo thời gian:

\[k=\frac{2\pi}{\lambda},\qquad\omega=\frac{2\pi}{T}.\]

Trong Matlab, sóng điều hoà hình sin \(\eqref{eq:6}\) có thể viết thành lệnh:

1
2
3
4
5
6
7
8
9
10
11
12
13

function psi = sin_wave(x)
%% sin wave
global v t
C = 5;
lambda = 5e-10;
k = 2*pi/lambda;
w = k*v;

lenx = length(x);
psi = zeros(1,lenx);
for i = 1:lenx
psi(i) = C*cos(k*x(i)-w*t);
end

Và cho ra kết quả mô phỏng như hình dưới.

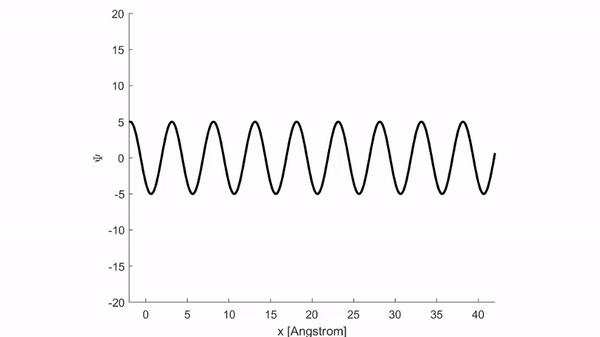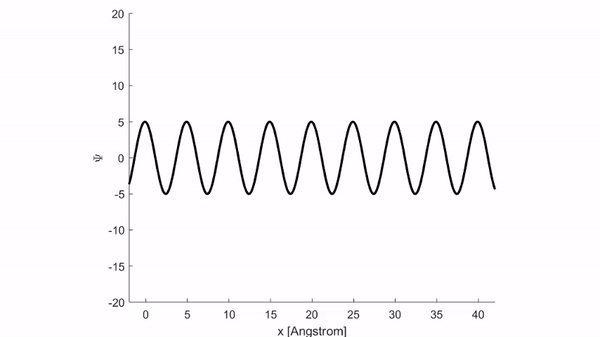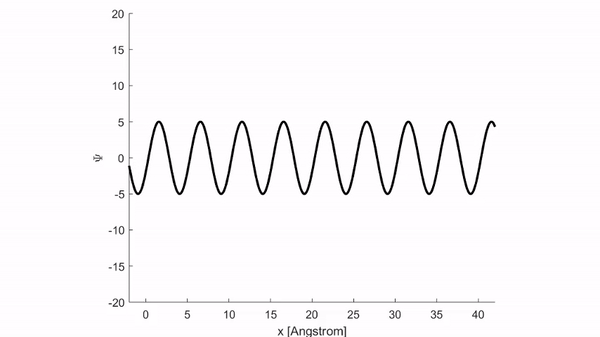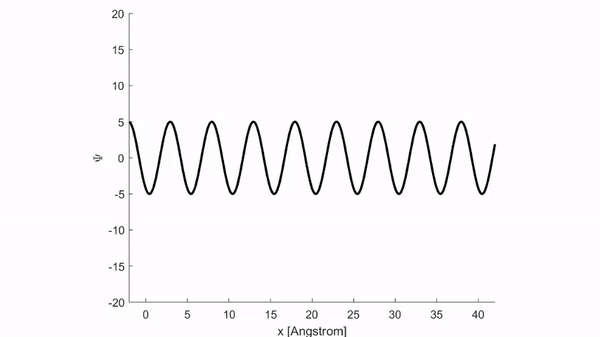
Thực tế cho thấy việc sử dụng hàm phức tỏ ra thuận tiện hơn nhiều so với hàm lượng giác. Do vậy trong cơ học lượng tử, người ta thường biểu diễn sóng sin \(\eqref{eq:6}\) dưới dạng hàm phức:

\[\psi(x,t)=Ce^{i(kx-\omega t)}.\label{eq:7}\tag{7}\]

Nguyên tắc của việc chuyển đổi này hết sức đơn giản: giá trị của hàm sóng chỉ thực sự nằm ở phần thực của hàm phức \(\eqref{eq:7}\):

\[Ce^{i(kx-\omega t)}=C[\cos(kx-\omega t)+i\cdot\sin(kx-\omega t)].\]

Để hiểu thêm về số phức và những thao tác trên nó, cần đọc bài “Hình học của số phức“.

Code chương trình

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

function wave_function
% Created by Tran Hai Cat
% 2019.03.03
clc;
clear variables
close all

global v t

%% CONSTANTS
h = 1.054e-34;
m = 9.1095e-31;
q_element = 1.6e-19;
Angstrom = 1e-10;

%% INPUT PARAMETRS
% Type of wave, choose one of:
% square_wave, triangle_wave, sin_wave
fun = 'square_wave';
E = 20*q_element;

xmin = -2*Angstrom;
xmax = 42*Angstrom;

%% DATA PROCESSING
x = linspace(xmin,xmax,500);
dt = 2e-19;

t = 0;
v = sqrt(2*E/m);

psi = feval(fun,x);

%% FIGURE
figure('name','Wave function','color','w','numbertitle','off');
hold on
line_psi = plot(x/Angstrom,real(psi),'linewidth',2,'color','k');
axis([xmin/Angstrom xmax/Angstrom -20 20]);
xlabel('x [Angstrom]');
ylabel('\Psi');

%% ANIMATION
while 1
t = t+dt;
psi = feval(fun,x);
set(line_psi,'ydata',psi);
pause(0.001);
end

function psi = square_wave(x)
%% square wave
global v t
C = 10;
a = 4e-10;
lenx = length(x);
psi = zeros(1,lenx);
for i = 1:lenx
if ((x(i)-v*t)>0) && ((x(i)-v*t)<a)
psi(i) = C;
end
end

function psi = triangle_wave(x)
%% triangle wave
global v t
C = 10;
a = 4e-10;
lenx = length(x);
psi = zeros(1,lenx);
k = C/a;
for i = 1:lenx
if ((x(i)-v*t)>0) && ((x(i)-v*t)<4e-10)
psi(i) = k*(x(i)-v*t);
end
end

function psi = sin_wave(x)
%% sin wave
global v t
C = 5;
lambda = 5e-10;
k = 2*pi/lambda;
w = k*v;

lenx = length(x);
psi = zeros(1,lenx);
for i = 1:lenx
psi(i) = C*cos(k*x(i)-w*t);
end

Bài mới

Hàm sóng

Code chương trình

Đáng chú ý

Trạng nguyên vật lý mùa 2

Giải nhất thực nghiệm Olympic vật lý quốc gia thuộc về sinh viên ngành cơ điện tử

ADN và cuốn sách cuộc đời

Giải thưởng vật lý danh giá cho nhà khoa học trẻ