Việc giải quyết các vấn đề thực tiễn, như giải phương trình sinh thái đề cập trong bài viết này, nhiều khi đưa về bài toán giải phương trình vi phân. Tuy nhiên trong nhiều tình huống, việc đi tìm nghiệm giải tích hết sức khó khăn và đôi khi không cần thiết. Ngày nay với công nghệ máy tính phát triển, các phương pháp tính toán số được ứng dụng rộng rãi. Python là một công cụ rất tốt để giải các bài toán đó.
Bài toán
Bài toán sau đây sẽ là một ví dụ cho thuật toán giải phương trình vi phân thông thường (ODE – Ordinary Differential Equation) thực thi trên Python. Vấn đề được trình bày theo tuần tự: Đặt vấn đề – Mô hình hoá – Thuật toán – Giải bằng Python.
Xét một hệ sinh thái đơn giản gồm thỏ và sói. Thỏ ăn cỏ để sống, còn sói chỉ ăn thịt thỏ. Số lượng bầy thỏ và bầy sói sẽ thay đổi như thế nào theo thời gian?
Bài toán sinh thái học này đã được nghiên cứu từ lâu và trở thành kinh điển trong các sách giáo khoa về các hệ động lực và cân bằng sinh thái. Số liệu thực nghiệm về quần thể thỏ – sói được ghi lại trong biểu đồ sau:
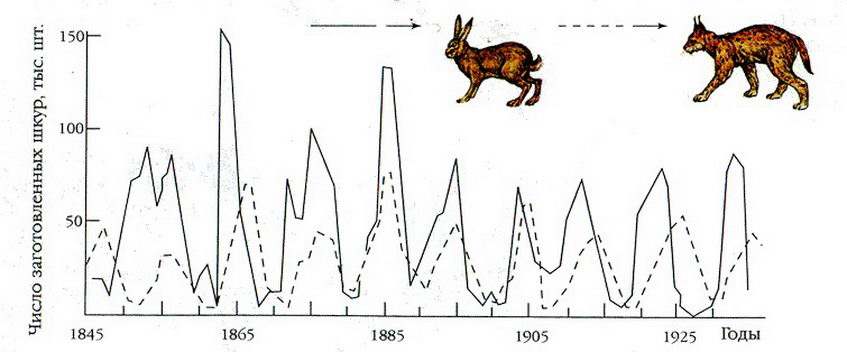
Dưới đây chúng ta sẽ lặp lại phân tích và giải thích diễn biến thực nghiệm ấy.
Mô hình hoá và thiết lập phương trình
Gọi \(y_1\) là số thỏ, \(y_2\) là số sói. Mục đích của chúng ta là tính số lượng thỏ và sói tại một thời điểm nào đó trong tương lai. Để làm được điều đó, ta cần đến hàm số miêu tả tốc độ biến đổi \(\frac{dy_1}{dt}\) và \(\frac{dy_2}{dt}\) theo thời gian.
Có thể xem rằng lượng cỏ đủ nhiều thỏ ăn mãi không hết. Thỏ mẹ sẽ sinh thỏ con, thỏ con lớn lên sẽ sinh thêm thỏ mới. Dễ hình dung rằng số lượng thỏ con sinh ra trong một đơn vị thời gian tỉ lệ với chính dân số bầy thỏ:
$$\frac{dy_1}{dt}=\alpha y_1,\tag{1}$$
trong đó \(\alpha\) – hệ số tỉ lệ phụ thuộc vào môi trường. Phương trình này có nghiệm giải tích đơn giản:
$$y_1=y_1(0)e^{\alpha t}.$$
Theo đó số thỏ không ngừng tăng lên theo hàm mũ! Thực tế tất nhiên không diễn ra như thế, thỏ sẽ bị sói ăn thịt bớt. Càng nhiều sói, thỏ càng bị ăn thịt nhiều. Ngoài ra số lượng thỏ bị ăn thịt cũng phải tỉ lệ với chính dân số của chúng. Phương trình (1) cần viết lại dưới dạng:
$$\frac{dy_1}{dt}=\alpha y_1-\beta y_1y_2.\tag{2}$$
Bây giờ xem qua đàn sói. Nếu không có thỏ sói sẽ bị thiếu thức ăn, lượng sói sẽ suy giảm với tốc độ tỉ lệ với chính dân số của chúng. Dân số càng cao thì số bị chết đi trong một đơn vị thời gian càng lớn:
$$\frac{dy_2}{dt}=-\gamma y_2.\tag{3}$$
Chúng sẽ chết dần theo quy luật:
$$y_2=y_2(0)e^{-\gamma t}.$$
Tất nhiên sói không chết hết mà vẫn duy trì quần thể nhờ ăn thịt thỏ. Thỏ càng nhiều, sói càng nhiều thức ăn và càng sinh sôi. Ngoài ra càng nhiều sói mẹ thì sói con cũng càng thêm được sinh ra. Phương trình (3) cần viết thành
$$\frac{dy_2}{dt}=-\gamma y_2+\delta y_1y_2.\tag{4}$$
Từ (2) và (4) ta có được hệ phương trình cần thiết:
$$\begin{aligned}\frac{dy_1}{dt}&=\alpha y_1-\beta y_1y_2,\\
\frac{dy_2}{dt}&=-\gamma y_2+\delta y_1y_2.\label{eq:lotka-volterra}\end{aligned}\tag{5}$$
Hệ phương trình này do Lotka và Volterra đưa ra vào năm 1925, được biết đến với tên gọi phương trình sinh thái Lotka-Volterra.
Giải phương trình sinh thái
Ta cần giải hệ phương trình (5) từ điều kiện sinh thái và số lượng thỏ – sói ban đầu. Hệ phương trình này viết bằng Python như sau:
import numpy as np
def model(y,t):
alpha = 0.07
beta = 0.0025
gamma = 0.2
delta = 0.003
dy_dt = (alpha-beta*y[1])*y[0]
d2y_dt2 = (-gamma+delta*y[0])*y[1]
return [dy_dt,d2y_dt2]Các tham số \(\alpha,\beta, \gamma, \delta\) được đưa vào hệ phương trình như những tham số bán thực nghiệm. Việc lấy tích phân sẽ bắt đầu với 30 con thỏ và 10 con sói:
y0 = [30,10]
Lấy khoảng thời gian khảo sát trong 200 tháng liên tục, chia làm 200 khoảng thời gian bằng nhau. Thư viện scipy.integrate của Python cho phép lấy nghiệm \(y_1\) và \(y_2\) tương ứng với hai hàm số thể hiện lượng thỏ và sói theo thời gian:
from scipy.integrate import odeint t = np.linspace(0,200,200) # Giải phương trình vi phân solve = odeint(model,y0,t) [y1,y2] = [solve.T[0],solve.T[1]]
Kết quả tính toán được thể hiện qua đồ thị bên dưới.
import plotly.graph_objects as go
import chart_studio.plotly as py
fig = go.Figure()
fig.add_trace(go.Scatter(x=t,y=y1,mode='lines+markers',name='Thỏ',
marker=dict(color='blue',line_width=0,line_color='blue'),
line=dict(color='red',width=1.5)))
fig.add_trace(go.Scatter(x=t,y=y2,mode='lines+markers',name='Sói',
marker=dict(color='red',line_width=0,line_color='red'),
line=dict(color='blue',width=1.5)))
fig.update_layout(title='Số lượng thỏ và sói theo thời gian',
xaxis_title='Thời gian [tháng]',
yaxis_title='Số lượng')Ta thấy rằng, một khi lượng thỏ tăng lên, sói cũng tăng lên theo dù chậm pha hơn một chút. Chính vì lượng sói tăng thêm này khiến số thỏ không thể tăng theo hàm mũ, mà tăng yếu dần rồi suy giảm. Lúc số thỏ đạt đỉnh cũng là khi lượng sói tăng nhanh nhất. Số thỏ giảm gây ra tổn thất cho bầy sói, làm cho bầy sói mất ăn, rồi cũng suy giảm theo một thời gian sau đó. Sói giảm, nguy cơ bớt đi, bầy thỏ lại sinh sôi. Và chu kì sinh giệt cứ lặp lại như cũ.
Đồ thị trực quan theo thời gian cung cấp cho ta một cái nhìn sinh động về chu kì sinh thái này.
Số lượng tương quan giữa thỏ và sói có thể quan sát qua đồ thị dưới. Có thể thấy được từ đồ thị này một cuộc rượt đuổi ngoạn mục của bầy thỏ và sói.
fig = go.Figure()
fig.add_trace(go.Scatter(x=y1,y=y2,mode='lines+markers',name='Thỏ',
marker=dict(color='blue',line_width=0,line_color='blue'),
line=dict(color='red',width=1.5)))
fig.update_layout(title='Tương quan số lượng thỏ - sói',
xaxis_title='Thỏ',
yaxis_title='Sói')
fig.update_yaxes(
scaleanchor = "x",
scaleratio = 1,
)Tác giả: Trần Hải Cát