Giải phương trình Schrodinger bằng phương pháp bắn tên

Ý tưởng

Trước hết cần nhắc lại phương trình Schrodinger:

\[-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}\Psi(x)+U(x)\Psi(x)=E\Psi(x).\]

hay viết dưới dạng thực hành:

\[\Psi”(x)=-k\left[E-U(x)\right]\Psi(x),\label{eq:1}\tag{1}\]

với \(k=\dfrac{2m}{\hbar^2}\). \(U(x)\) là hàm thế năng có phương trình phụ thuộc vào hình dạng của hố thế.

Trong bài “Phương trình dừng Schrodinger” chúng ta đã bàn về nguyên lý chung của việc giải phương trình Schrodinger bằng “phương pháp bắn tên”. Ý tưởng cơ bản của phương pháp bắn tên nằm ở chỗ: một mũi tên bắn đi với điều kiện ban đầu:

\[\begin{cases}\Psi(-\infty)=0,\\ \Psi'(-\infty)=0.\end{cases}\]

Ta cần tìm giá trị của năng lượng \(E\) sao cho mũi tên bắn “trúng đích”:

\[\Psi(+\infty)=0.\]

Tuy nhiên trên thực tế trong nhiều trường hợp, việc truy tìm giá trị năng lượng \(E\) khá vất vả, bởi hàm \(\Psi\) khó hội tụ. Bài viết này sẽ bàn đến một phương pháp khác có thể giải quyết được vướng mắc ấy.

Khác với phương pháp cũ, ở đây ta cũng dùng phép “bắn tên”, nhưng bắn đồng thời từ hai hướng khác nhau. Ý tưởng mô tả như hình 1.

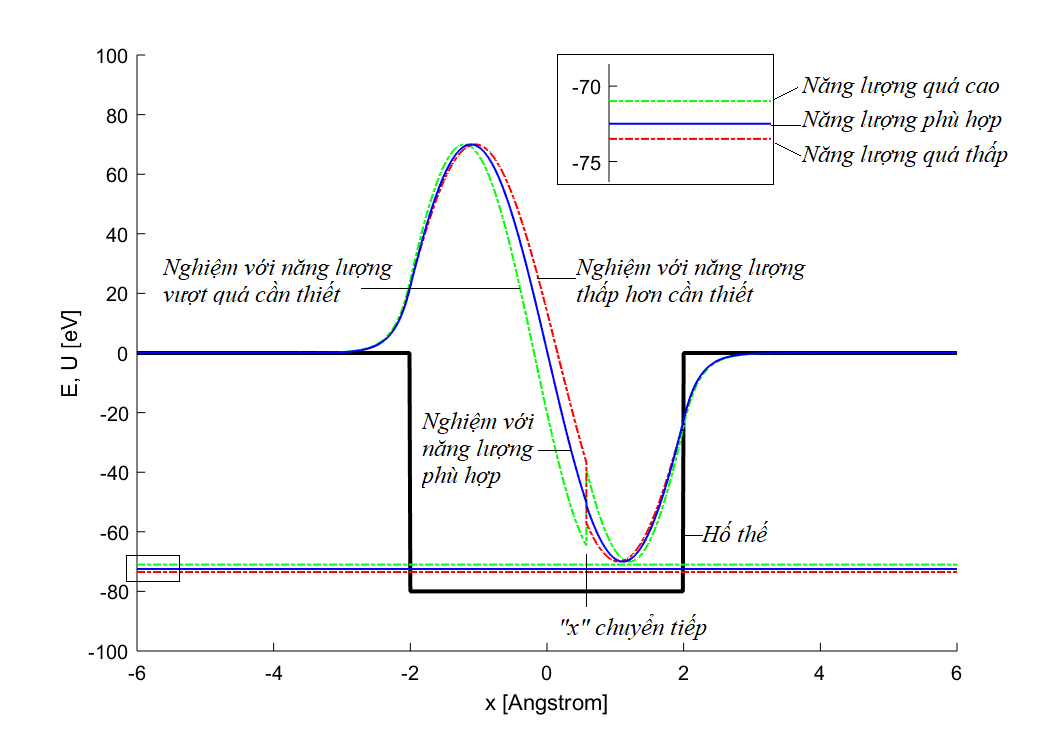
Hình 1: Ý tưởng giải phương trình Schrodinger

Một mặt, ta bắn một mũi tên từ rìa hố thế bên trái với điều kiện ban đầu:

\[\begin{cases}\Psi(-\infty)\approx\Psi(\mathrm{xmin})=10^{-10},\\ \Psi'(-\infty)\approx\Psi'(\mathrm{xmin})=10^{-10}.\end{cases}\]

Mặt khác, ta cũng bắn một mũi tên khác từ rìa hố thế bên phải theo chiều ngược lại, với điều kiện ban đầu:

\[\begin{cases}\Psi(+\infty)\approx\Psi(\mathrm{xmax})=10^{-10},\\ \Psi'(+\infty)\approx\Psi'(\mathrm{xmax})=10^{-10}.\end{cases}\]

Nếu quỹ đạo của hai mũi tên này hợp thành một đường liên tục và cong trơn, ta có thể kết luận rằng đó là một nghiệm phù hợp với trạng thái dừng.

Thực hiện trên Matlab

Phương trình Schrodinger \eqref{eq:1} nên viết lại thành hệ phương trình vi phân bậc nhất:

\[\begin{cases}\dfrac{dy_1}{dx}=y_2,\\ \dfrac{dy_2}{dx}=-k\left[E-U(x)\right]y_1.\end{cases}\label{eq:2}\tag{2}\]

Trong đó:

\[\begin{cases}y_1=\Psi(x),\\ y_2=\Psi'(x),\end{cases}\]

Hệ phương trình \eqref{eq:2} trình bày theo code Matlab như sau:

1
2
3
4
5
6

function dy = schrodinger(x,y)
%% Schrodinger Equation
global E k U0 x1 x2
dy = zeros(2,1);
dy(1) = y(2);
dy(2) = -k<em>(E-U_square(U0,x1,x2,x))</em>y(1);

Kí hiệu \(\mathrm{dy(1)}\) biểu thị cho đạo hàm bậc nhất \(\Psi'(x)\), còn \(\mathrm{dy(2)}\) biểu thị cho đạo hàm bậc hai \(\Psi”(x)\). Hàm \(\mathrm{U\_square(U0,x1,x2,x)}\) sử dụng ở đây chỉ là một ví dụ dành cho hố thế vuông với định nghĩa:

\[\begin{cases}U=U_0&\mathrm{khi}\ x\in(x_1,x_2),\\ U=0&\mathrm{khi}\ x\notin(x_1,x_2).\end{cases}\]

Trên Matlab hàm thế năng \(U(x)\) trên thực hiện qua function:

1
2
3
4
5
6
7
8
9
10
11

function y = U_square(U0,x1,x2,x)
%% Potential Energy
lenx = length(x);
y = zeros(1,lenx);
for i = 1:lenx
if(x(i)<=x1)||(x(i)>=x2)
y(i) = 0;
else
y(i) = U0;
end
end

Với những trường hợp hố thế khác, như hố parabol, hố tuần hoàn… người viết chương trình có thể định nghĩa hàm thế năng \(U(x)\) theo dạng khác.

Mũi tên bắn từ rìa bên trái của hố thế được thực hiện thông qua việc giải phương trình vi phân bằng phương pháp Runge-Kutta bậc 4-5:

1	[x_left,psi_left] = ode45(@Schrodinger,linspace(xmin,x_inter,500),[psi psi1]);

Trong đó \(\mathrm{xmin}\) là vị trí đủ xa về bên trái sao cho có thể xem như \(\mathrm{xmin}=-\infty\). Còn \(\mathrm{x\_inter}\) là điểm trung gian chọn đâu đó nằm gần giữa hố thế. \(\mathrm{psi}\) và \(\mathrm{psi1}\) giúp khai báo điều kiện ban đầu của \(\Psi\) và \(\Psi’\), với giá trị đủ nhỏ:

\[\begin{cases}\Psi(-\infty)\approx\Psi(\mathrm{xmin})=10^{-10},\\ \Psi'(-\infty)\approx\Psi'(\mathrm{xmin})=10^{-10}.\end{cases}\]

Mũi tên bắn từ rìa bên phải của hố thế cũng tiến hành tương tự theo hướng ngược lại:

1	[x_right,psi_right] = ode45(@Schrodinger,linspace(xmax,x_inter,500),[psi psi1]);

Trong đó \(\mathrm{xmax}\) là vị trí đủ xa về phía bên phải sao cho có thể xem như \(\mathrm{xmax}=+\infty\). \(\mathrm{psi}\) và \(\mathrm{psi1}\) giúp khai báo điều kiện ban đầu của \(\Psi\) và \(\Psi’\), với giá trị đủ nhỏ:

\[\begin{cases}\Psi(+\infty)\approx\Psi(\mathrm{xmax})=10^{-10},\\ \Psi'(+\infty)\approx\Psi'(\mathrm{xmax})=10^{-10}.\end{cases}\]

Cuối cùng ghép hai quỹ đạo từ hai mũi tên bằng lệnh:

1 2	X = [x_left;flipud(x_right)]; Psi = [psi_left(:,1);flipud(psi_right(:,1))];

Ta sẽ thu được hàm biên độ \(\Psi(x)\) như trên hình 1. Hình 1 cũng miêu tả 3 tình huống khác nhau của năng lượng \(E\), tương ứng với 3 nghiệm. Có thể thấy rằng, chỉ với mức năng lượng \(E\) nhất định nào đó, phương trình Schrodinger mới cho ra nghiệm cong trơn tự nhiên.

Có thể tổng kết lại quy trình giải phương trình dừng Schrodinger bằng phương pháp bắn tên như sau:

Bước 1: Chọn giá trị \(\mathrm{x\_inter}\) đóng vai trò làm vị trí chuyển tiếp, ranh giới giữa hai làn đạn.
Bước 2: Gán giá trị năng lượng \(E\) sát gần đáy hố thế, cao hơn đáy chỉ một chút.
Bước 3: Chọn vị trí \(\mathrm{xmin}\) đủ xa về phía bên trái của hố thế, sao cho có thể xem như \(\mathrm{xmin}\approx -\infty\). Cũng như chọn vị trí \(\mathrm{xmax}\) đủ xa về phía bên phải của hố thế, sao cho có thể xem như \(\mathrm{xmax}\approx +\infty\).
Bước 4: Tiến hành hai lần giải phương trình vi phân \eqref{eq:1} với giá trị năng lượng \(E\) đã cho. Một lần cho mũi tên bắn từ bên trái, lần hai cho mũi tên bắn từ bên phải.
Bước 5: Nối hai quỹ đạo thành nghiệm \(\Psi(x)\). Nếu \(\Psi(x)\) bị gãy khúc tại vị trí \(\mathrm{x\_inter}\), có thể suy rằng nó không phải là nghiệm của phương trình Schrodinger. Ngược lại, nếu \(\Psi(x)\) là đường cong trơn, chứng tỏ nó là nghiệm.
Nếu \(\Psi(x)\) vừa tính được không phải nghiệm, chứng tỏ năng lượng \(E\) không phải giá trị phù hợp, ta có thể nâng \(E\) lên một chút và lặp lại quy trình giải, cho đến khi nào tìm thấy nghiệm phù hợp.

Code chương trình Matlab

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

function Schrodinger_solve_model_2
% Created by Tran Hai Cat
% 2019.04.15
clc;
clear variables
close all

global E k U0 x1 x2

%% CONSTANTS
h = 1.054e-34;
m = 9.1095e-31;
q_element = 1.6e-19;
Angstrom = 1e-10;
k = 2*m/h/h;

%% INPUT PARAMETRS
% Nang luong, tuy chon de tim ra muc phu hop:
E = -72.369*q_element;

% Tham so cua ho the:
U0 = -80*q_element;
x1 = -2*Angstrom;
x2 = 2*Angstrom;

% Tham so tinh toan & gioi han khung hinh:
Emin = -100*q_element;
Emax = 100*q_element;
xmin = -6*Angstrom;
xmax = 6*Angstrom;
% Diem noi trung gian, chon bat ki:
x_inter = 0.5769*Angstrom;

% Dieu kien ban dau cua bai toan Cauchy:
psi = 1e-10; % \psi
psi1 = 0; % \psi'

%% CALCULATION
[x_left,psi_left] = ode45(@Schrodinger,linspace(xmin,x_inter,500),[psi psi1]);
[x_right,psi_right] = ode45(@Schrodinger,linspace(xmax,x_inter,500),[psi psi1]);
psi_right = sign(psi_left(end,2)*psi_right(end,2))*psi_right;
% Nghiem thu duoc:
X = [x_left;flipud(x_right)];
Psi = [psi_left(:,1);flipud(psi_right(:,1))];

% Chuan hoa ham song:
S_norm = trapz(X,conj(Psi).*Psi);
Psi = Psi/sqrt(S_norm);

% Tao Psi_draw de ve cho vua voi khung do thi nang luong:
Psi_max = max(Psi);
Psi_draw = 0.7*Psi/Psi_max*Emax/q_element;
psi_psi = 0.8*(Psi.^2/Psi_max/Psi_max*Emax/q_element);

% Tinh dt phu hop cho dao dong:
omega = abs(E)/h;
T = 2*pi/omega;
dt = T/1000;
t = 0;

%% FIGURE
x_plot = linspace(xmin,xmax,1000);
U_plot = U_square(U0,x1,x2,x_plot);

figure('name','Standing_wave_potential_well',...
'color','black','numbertitle','off');
hold on
plot(x_plot/Angstrom,U_plot/q_element,'linewidth',2,'color','w');
line([xmin/Angstrom,xmax/Angstrom],[E/q_element,E/q_element],...
'linewidth',2,'color','b');
line_psi = plot(X/Angstrom,Psi_draw,'linewidth',1,'color','y');
plot(X/Angstrom,psi_psi,'linewidth',1);
title(sprintf('E = %0.3f [eV]',E/q_element),'color','w');
axis([xmin/Angstrom xmax/Angstrom Emin/q_element Emax/q_element]);
set(gca,'color','k','xcolor','w','ycolor','w')
xlabel('x [Angstrom]');
ylabel('E, U [eV]');

% while 1
% t = t+dt;
% Psi_time = Psi_draw*exp(-1i*omega*t);
% set(line_psi,'ydata',real(Psi_time));
% pause(0.001);
% end

function dy = Schrodinger(x,y)
%% Schrodinger Equation
global E k U0 x1 x2
dy = zeros(2,1);
dy(1) = y(2);
dy(2) = -k*(E-U_square(U0,x1,x2,x))*y(1);

function y = U_square(U0,x1,x2,x)
%% Potential Energy
lenx = length(x);
y = zeros(1,lenx);
for i = 1:lenx
if(x(i)<=x1)||(x(i)>=x2)
y(i) = 0;
else
y(i) = U0;
end
end

Bài mới

Giải phương trình Schrodinger bằng phương pháp bắn tên

Ý tưởng

Thực hiện trên Matlab

Code chương trình Matlab

Đáng chú ý

Đại học Sư phạm Kỹ thuật Tp.HCM đăng cai Hội nghị Vật lý chất rắn và khoa học vật liệu lần thứ XIII

Trạng nguyên vật lý mùa 2

Giải nhất thực nghiệm Olympic vật lý quốc gia thuộc về sinh viên ngành cơ điện tử

ADN và cuốn sách cuộc đời