Bó sóng với rào thế bậc thang

Trong bài giảng về sự tương tác của sóng de-Broglie với rào thế bậc thang, có thể hiểu rằng đó là tương tác giữa một chùm hạt đồng nhất lên rào thế. Để hiểu rõ ý nghĩa của tương tác này, ta sẽ đi xây dựng mô hình bó sóng với rào thế bậc thang, đặc trưng cho một hạt lao về phía rào thế.

Hãy khảo sát một bó sóng hình chuông, đặc trưng cho một hạt đang chuyển động với năng lượng \(E\) và xung lượng \(p=\sqrt{2mE}\). Tại thời điểm ban đầu \(t=0\) sóng có dạng hàm:

\[\psi(x,0)=Ae^{-x^2/4\sigma_x^2}e^{i(\frac{p}{\hbar}x-\frac{E}{\hbar}0)}.\label{eq:1}\tag{1}\]

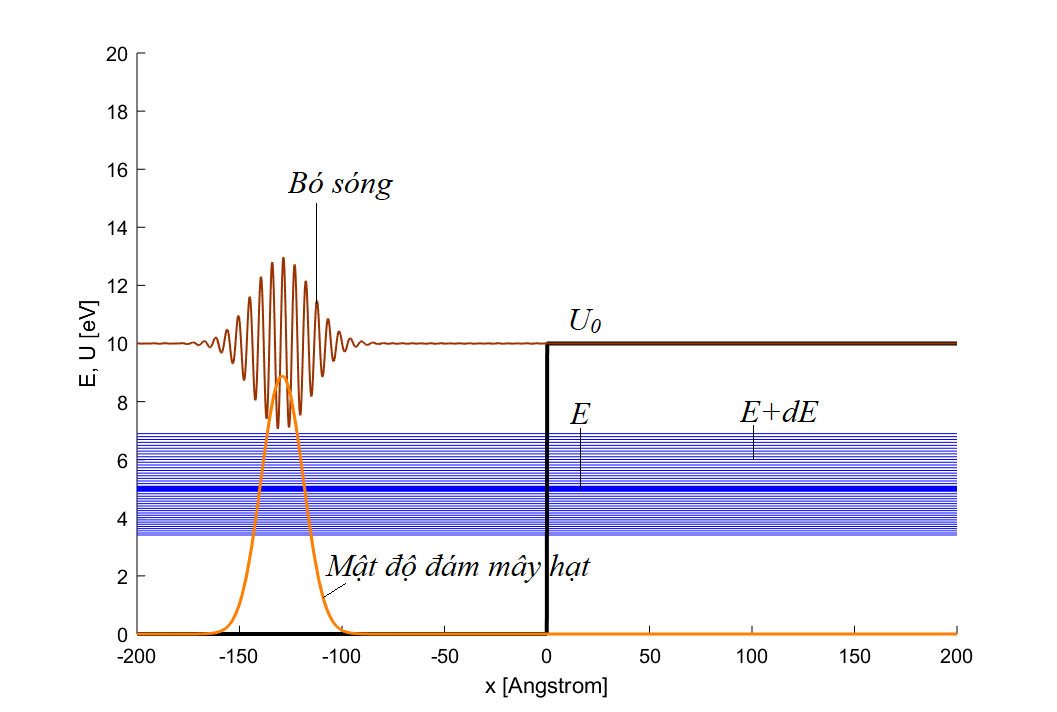
Hàm sóng \eqref{eq:1} được diễn tả như hình 1, với độ bất định vị trí \(\sigma_x=10\,\mathrm{A}\). Mật độ của hạt lúc \(t=0\)

\[\psi(x,0)^*\psi(x,0)=Ae^{-x^2/2\sigma_x^2}\]

có dạng của phân bố Gauss với độ lệch chuẩn bằng \(\sigma_x\), diễn tả qua đường màu cam trên hình 1. Như vậy, hàm sóng \eqref{eq:1} diễn tả một “đám mây” hạt mà có đến \(70\,\%\) khối lượng của nó hội tụ quanh vị trí \(x=x_0\) trong vòng bán kính \(\sigma_x\).

Để biết được bó sóng sẽ di chuyển như thế nào, ta cần phân tích bó sóng thành sự chồng chập của nhiều sóng de-Broglie tại thời điểm \(t=0\), bởi vì sóng de-Broglie có quy luật vận động rõ ràng. Thực vậy, qua bài Sóng de-Broglie với rào thế bậc thang, sóng được hình thành từ sóng tới, sóng phản xạ và sóng truyền qua:

\[\begin{cases}\psi_{in}(x,t)=e^{i(\frac{p_1}{\hbar}x-\frac{E}{\hbar}t)}\\ \psi_{ref}(x,t)=\dfrac{p_1-p_2}{p_1+p_2}e^{i(-\frac{p_1}{\hbar}x-\frac{E}{\hbar}t)},\\ \psi_{tran}(x,t)=\dfrac{2p_1}{p_1+p_2}e^{i(\frac{p_2}{\hbar}x-\frac{E}{\hbar}t)},\end{cases}\label{eq:2}\tag{2}\]

với \(p_1=\sqrt{2mE}, p_2=\sqrt{2m(E-U_0)}\). Ta sẽ khai triển bó sóng \eqref{eq:1} tại thời điểm \(t=0\) thành sự chồng chập của nhiều sóng de-Broglie dạng \eqref{eq:2}:

\[\psi(x,0)=\int\limits_{-\infty}^{\infty}{C(p)\left[\psi_{in}(x,0)+\psi_{ref}(x,0)\right]\,dp},\]

Phép phân tích này chỉ bao gồm sóng tới \(\psi_{in}(x,0)\) và sóng phản xạ \(\psi_{ref}(x,0)\), bởi ban đầu khi \(t=0\) bó sóng hoàn toàn nằm trong phạm vi của sóng tới và sóng phản xạ, tức vùng 1. Các hệ số \(C(p)\) được tính toán theo phép biến đổi Fourier:

\[\begin{aligned}C(p)&=\frac{1}{2\pi\hbar}\int\limits_{-\infty}^{\infty}{\left[\psi_{in}^(x,0)+\psi_{ref}^(x,0)\right]\psi(x,0)\,dx},\\&=\frac{1}{2\pi\hbar}\int\limits_{-\infty}^{\infty}{\left[e^{-i\frac{p_1}{\hbar}x}+\frac{p_1-p_2}{p_1+p_2}e^{i\frac{p_1}{\hbar}x}\right]\psi(x,0)\,dx}.\end{aligned}\label{eq:3}\tag{3}\]

Kết quả tính toán cho \(C(p)\) thể hiện trên hình 2:

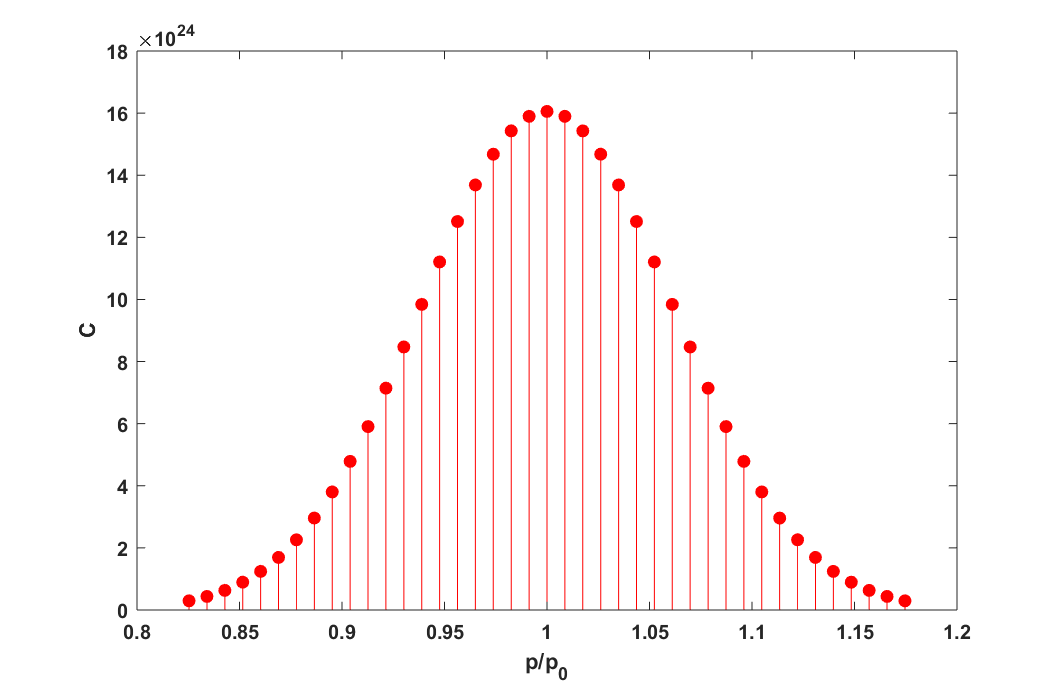
Trạng thái của bó sóng thời điểm \(t\) bất kì là sự tổng hợp các sóng de-Broglie trở lại:

\[\begin{cases}\psi(x,t)=\int\limits_{-\infty}^{\infty}{C(p)\left[\psi_{in}(x,t)+\psi_{ref}(x,t)\right]dp} & \mathrm{khi}\ x<0,\\ \psi(x,t)=\int\limits_{-\infty}^{\infty}{C(p)\psi_{tran}(x,t)\,dp} & \mathrm{khi}\ x>0.\end{cases}\]

với các hệ số \(C(p)\) đã tính được từ phép biến đổi \eqref{eq:3}. Sử dụng code chương trình Matlab bên dưới, ta có thể thực hiện chuỗi tính toán trên bằng máy tính.

Video sau đây biểu diễn kết quả tính toán cho trường hợp hạt có năng lượng cao hơn rào thế: \(E>U_0\). Theo cơ học cổ điển, hạt sẽ di chuyển dễ dàng qua rào thế và đi tiếp. Còn ở đây, trong thế giới lượng tử, hạt chỉ đi qua một phần, còn một phần bị phản xạ ngược!

Video tiếp theo lại minh hoạ kết quả tính toán cho trường hợp hạt có năng lượng \(E\) thấp hơn chiều cao rào thế. Theo cơ học cổ điển, hạt sẽ bị dội ngược lại do không đủ năng lượng để leo lên. Trong cơ học lượng tử cũng xảy ra tình huống tương tự: hạt bị phản xạ toàn phần!

Code chương trình Matlab

• Hàm sóng
• Sóng de Broglie
• Nguyên lý bất định Heisenberg
• Phương trình Schrodinger
• Sóng de-Broglie với rào thế bậc thang
• Bó sóng với rào thế bậc thang
• Sự hình thành trạng thái dừng nguyên tử
• Phương trình dừng Schrodinger
• Giải phương trình Schrodinger bằng phương pháp bắn tên
• Trạng thái dừng trong hố thế vuông
• Dao động tử điều hoà – Phần 1
• Dao động tử điều hoà – Phần 2
• Máy phân tích phổ nhiễu xạ – Toán tử động lượng
• Máy phân tích quang phổ – Toán tử năng lượng
• Đại lượng có giá trị xác định đồng thời
• Mô-men động lượng
• Nguyên tử hidro trong trường hợp đối xứng cầu
• Nguyên tử hidro trường hợp tổng quát
• Đề cương ôn tập Cơ học lượng tử & Vật lý nguyên tử