Bài 26D: Khảo sát quá trình nạp xả tụ trong mạch RC qua biến thiên dòng điện

MỤC ĐÍCH

Quan sát quá trình nạp xả tụ qua việc đo dòng điện nạp và dòng điện xả. Phân tích quy luật suy giảm của dòng điện cho phép xác định hằng số thời gian của mạch \(RC\).

MẠCH \(RC\)

Mạch \(RC\) cấu tạo gồm tụ có điện dung \(C\) và điện trở \(R\) mắc nối tiếp. Trong quá trình nạp tụ, ta cho hai đầu mạch này nối vào nguồn có sức điện động \(E\) như hình 1. Điện tích sẽ thông qua điện trở \(R\) tích lên các bản tụ. Ngược lại, khi xả tụ, ta nối trực tiếp hai đầu mạch với nhau như hình 4. Điện tích có trên các bản tụ sẽ đi theo chiều ngược lại, thông qua điện trở \(R\) và trung hoà.

Quá trình nạp tụ

Xét trạng thái ban đầu, khi chưa có điện tích trên tụ \(C\), ta đóng khoá \(K\) theo sơ đồ hình 1. Sẽ có một dòng điện \(I(t)\) theo chiều kim đồng hồ, đưa điện tích dương từ bản tụ phải qua bản tụ trái.

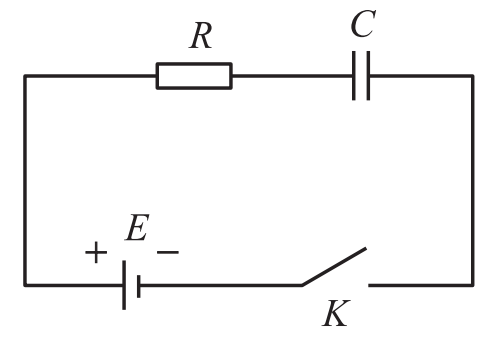
Áp dụng định luật Kirchhoff cho các hiệu điện thế:

\[IR+U_C=E,\]

với \(U_C=q/C\) là hiệu điện thế hai đầu tụ. Biểu diễn dòng điện qua đạo hàm của điện tích, viết lại:

\[\frac{dq}{dt}R+\frac{q}{C}=E.\]

Thu được phương trình vi phân bậc nhất của điện tích \(q\) theo thời gian:

\[\frac{dq}{dt}+\frac{q}{RC}=\frac{E}{R}.\]

Phương trình này có nghiệm:

\[q(t)=CE\left[1-\exp\left(-\frac{t}{RC}\right)\right].\label{eq:1}\tag{1}\]

Ở đây \(q_0=CE\) – điện tích tối đa mà tụ \(C\) có thể nạp với sức điện động này, \(\tau=RC\) – hằng số thời gian – miêu tả thời gian để tụ nạp đến \((1-1/\mathrm{e})=63\%\) dung lượng cực đại.

Hàm \(\eqref{eq:1}\) được miêu tả trên đồ thị hình 2. Theo lý thuyết, thời gian nạp tụ lâu vô cùng. Tuy vậy trong kĩ thuật, người ta thường lấy khoảng thời gian \(3\tau\), đủ nạp đến \(95\%\) hoặc \(5\tau\), đủ nạp đến \(99.3\%\) để đánh giá thời gian nạp tụ.

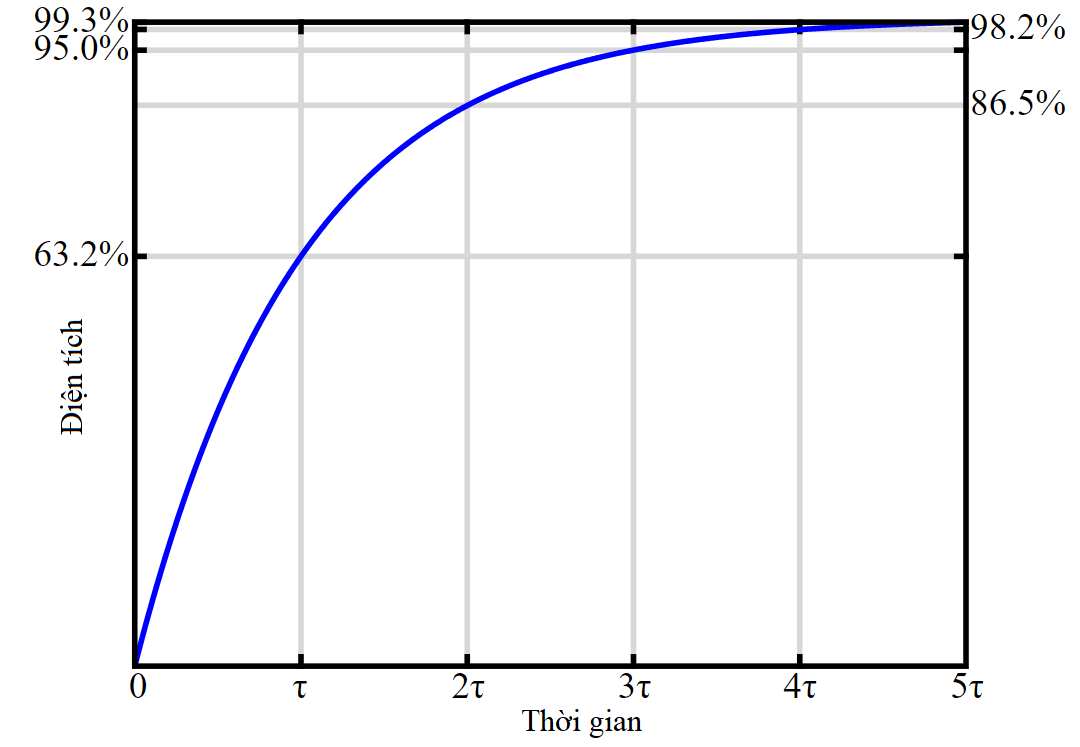
Lấy đạo hàm của \(\eqref{eq:1}\) theo thời gian, ta có được quy luật biến thiên của dòng điện nạp:

\[I(t)=I_0\exp\left(-\frac{t}{RC}\right),\label{eq:2}\tag{2}\]

trong đó \(I_0=\frac{E}{R}\) – dòng điện ban đầu. Hàm \(I(t)\) miêu tả dưới đồ thị hình 3. Hằng số \(\tau=RC\) lúc này miêu tả thời gian để dòng nạp suy giảm \(\mathrm{e}\approx 2.7\) lần, chỉ còn \(37\%\) so với ban đầu.

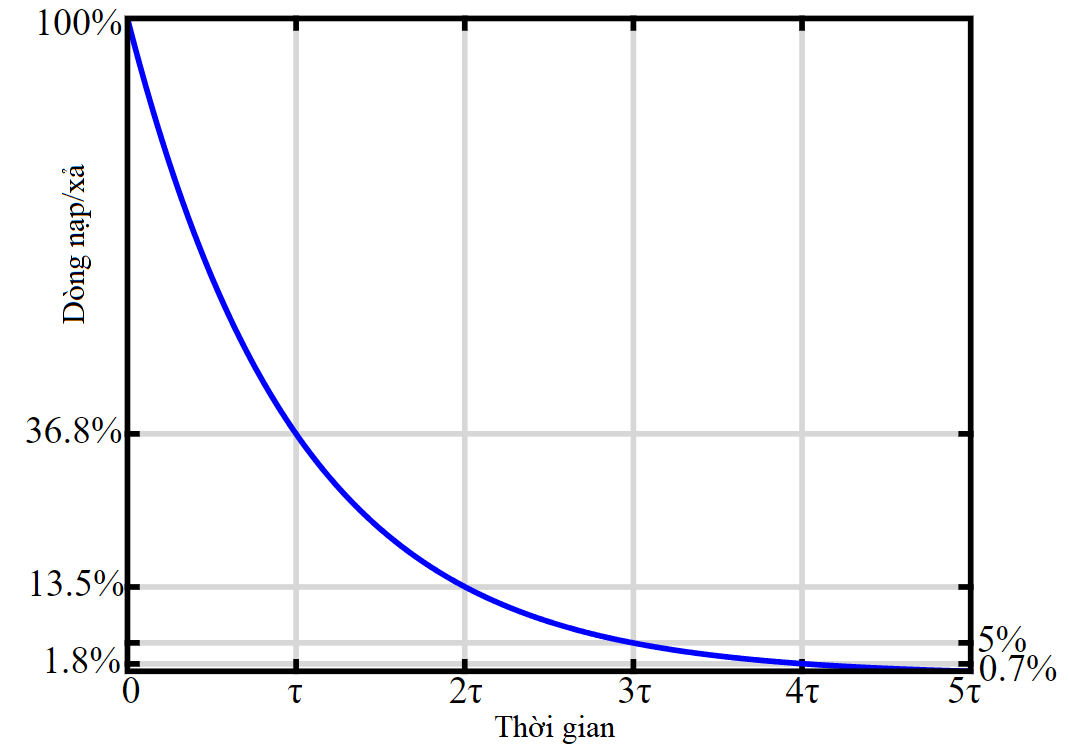
Ta thấy rằng, dòng nạp xuất hiện đột ngột lên một giá trị lớn bằng \(I_0=E/R\), rồi suy giảm dần trong quá trình nạp tụ. Khi tụ càng đầy, dòng nạp càng bé đi. Nhìn chung dòng nạp chỉ xuất hiện khi chuyển điện tích lên các bản tụ. Lúc ổn định tụ không cho phép dòng không đổi chạy qua.

Quá trình xả tụ

Trạng thái ban đầu của hệ trước khi đóng khoá \(K\) (hình 4) là tụ \(C\) đang chứa điện tích \(q_0\). Khi đóng khoá, sẽ có một dòng điện \(I(t)\) theo chiều từ bản dương sang bản âm, đưa điện tích của tụ về 0.

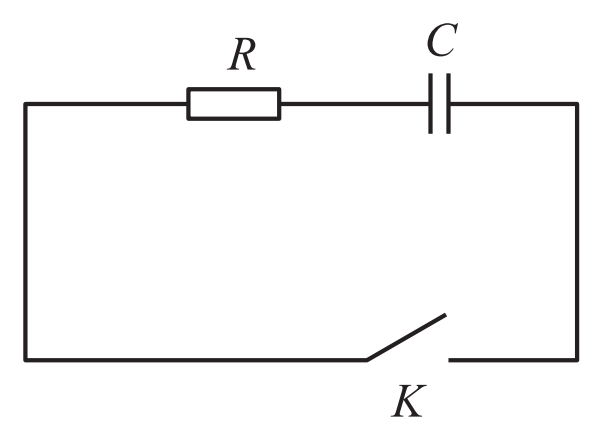
Phương trình Kirchhoff cho quá trình xả tụ không còn chứa nguồn:

\[IR+U_C=0,\]

hay:

\[\frac{dq}{dt}R+\frac{q}{C}=0.\]

Ta viết thành phương trình vi phân bậc nhất của điện tích \(q\) theo thời gian:

\[\frac{dq}{dt}+\frac{q}{RC}=0.\]

Phương trình này có nghiệm:

\[q(t)=q_0\exp\left(-\frac{t}{RC}\right).\label{eq:3}\tag{3}\]

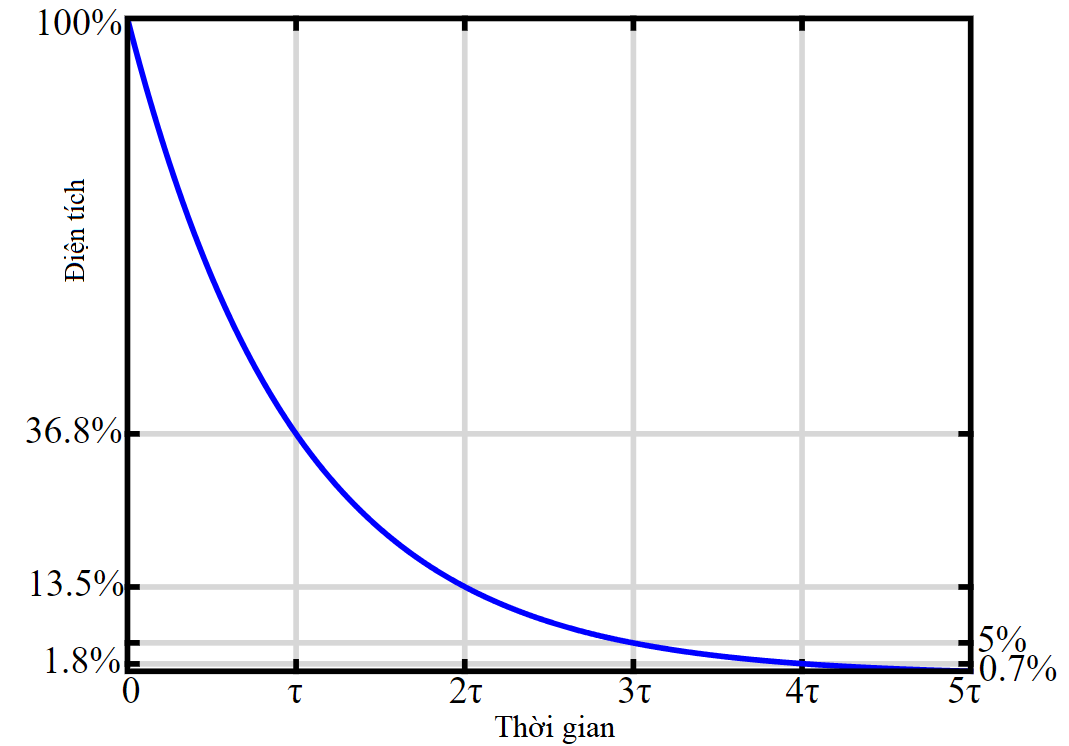
Hình 5 miêu tả quy luật suy giảm điện tích khi xả tụ. Hằng số \(\tau=RC\) miêu tả thời gian để điện tích suy giảm \(\mathrm{e}\approx 2.7\) lần, chỉ còn \(37\%\) so với ban đầu. Theo lý thuyết, thời gian xả tụ lâu vô cùng. Nhưng các nhà kĩ thuật thường chọn \(3\tau\), khi xả còn chỉ \(5\%\) hoặc \(5\tau\), khi xả còn \(0.7\%\) để đánh giá thời gian xả tụ.

Lấy đạo hàm của \(\eqref{eq:3}\) theo thời gian, ta có được quy luật biến thiên của dòng điện xả:

\[I(t)=I_0\exp\left(-\frac{t}{RC}\right),\label{eq:4}\tag{4}\]

với \(I_0\) – cường độ dòng điện khi bắt đầu xả tụ. Hàm \(I(t)\) có đồ thị hoàn toàn tương tự hình 3. Tuy vậy cần lưu ý rằng, tuy có điểm chung đều xuất hiện đột ngột với giá trị lớn rồi giảm dần, nhưng hai dòng nạp xả này có chiều ngược nhau.

NGUYÊN LÝ THÍ NGHIỆM

Mạch thí nghiệm với tụ \(C\) và điện trở \(R\) mắc nối tiếp vào hai chân cầu dao \(AB\) như sơ đồ dưới. Khi cần nạp tụ, ta đẩy cầu dao tiếp xúc với nguồn thông qua chân \(XY\). Khi cần xả tụ, ta đẩy cầu dao tiếp xúc với hai chân \(EF\), về bản chất là nối đoản mạch \(AB\) thông qua \(EF\). Am-pe kế giúp quan sát cụ thể biến thiên của dòng điện theo thời gian.

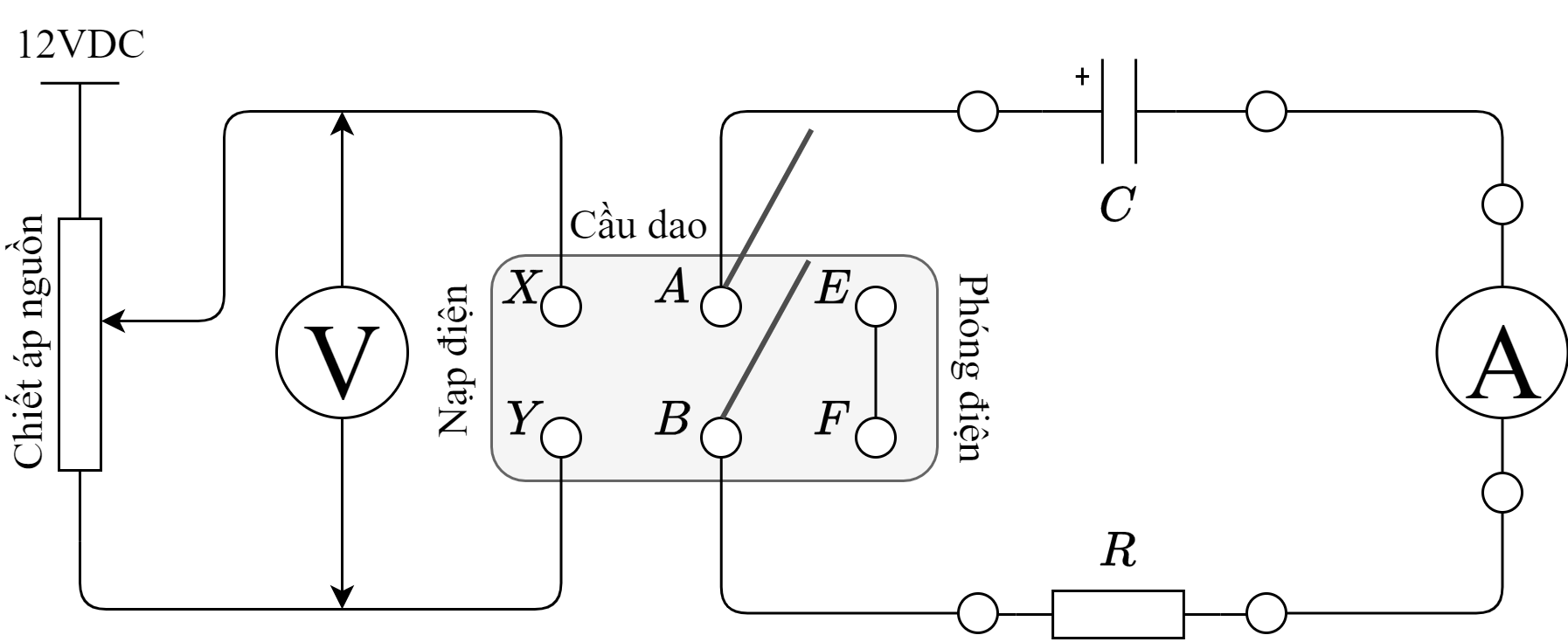
Trong thí nghiệm này, với điện áp nguồn cho trước, quá trình nạp/xả tụ tiến hành qua cầu dao. Đại lượng cần ghi chép là hàm số \(I(t)\) đo bằng đồng hồ bấm giờ và am-pe kế. Từ hàm số \(I(t)\) thu được, ta có thể nghiệm lại quy luật biến thiên hàm mũ \(\eqref{eq:2}\) và \(\eqref{eq:4}\), sau đó tính hằng số thời \(\tau\) và so sánh với giá trị lý thuyết \(\tau=RC\).

Quá trình tích điện khi nạp tụ có thể tính được qua tích phân:

\[q(t)=\int\limits_0^t{I(t)\,dt}.\label{eq:5}\tag{5}\]

Từ đây ta có thể nghiệm lại quy luật \(\eqref{eq:1}\).

QUY TRÌNH THÍ NGHIỆM

Nhận từ giáo viên các tổ hợp linh kiện \(R\) và \(C\). Mỗi tổ hợp cần chuẩn bị 2 bảng số liệu ghi lại dòng điện theo thời gian, một nạp và một xả. Suốt quá trình thí nghiệm giữ nguyên mức điện áp nguồn do giáo viên chỉ định.

\[ \text{Nạp tụ}\\ \text{\(C=\ldots\quad R=\ldots\)}\\ \begin{array}{c|c} \hline \text{\(t\) (\(\mathrm{s}\))} & \text{\(I\) (\(\mathrm{\mu A}\))} & \text{\(\ln{I}\)} & \text{\(q\) (\(\mathrm{\mu C}\))}\\ \hline 0 & &\\ 20 & &\\ 40 & &\\ … & … & … \\ \hline \end{array}\\ \]\[ \text{Xả tụ}\\ \text{\(C=\ldots\quad R=\ldots\)}\\ \begin{array}{c|c} \hline \text{\(t\) (\(\mathrm{s}\))} & \text{\(I\) (\(\mathrm{\mu A}\))} & \text{\(\ln{I}\)} \\ \hline 0 & &\\ 20 & &\\ 40 & &\\ … & … & … \\ \hline \end{array}\\ \]

Mắc tụ \(C\) và điện trở \(R\) vào mạch như sơ đồ hình 6 và tiến hành thí nghiệm nạp tụ và xả tụ như bên dưới. Đặc biệt lưu ý chiều âm dương của tụ theo sơ đồ.

Nạp tụ

Cầu dao để hở không tiếp xúc. Am-pe kế cắm đúng chân để dòng nạp có thể di chuyển theo chiều kim đồng hồ. Đưa am-pe kế về thang đo \(\mu A\). Chuẩn bị đồng hồ bấm giây ở chế độ chờ.

Dùng dây điện (hoặc thanh kim loại) để nối đoản mạch hai chân tụ, đảm bảo tụ được xả hết điện tích trước khi nạp. Sau đó bỏ dây đoản mạch ra và bắt đầu phép đo.

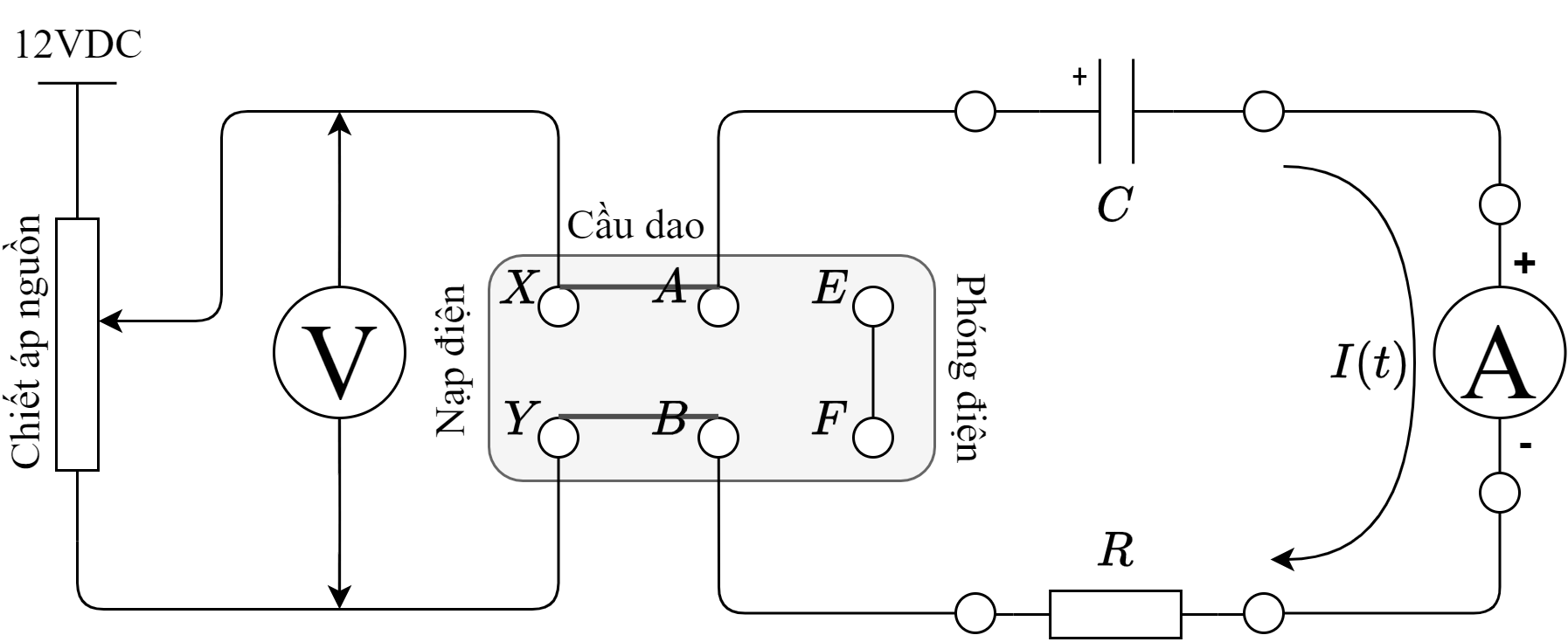
Đưa hai chân \(AB\) của cầu dao tiếp xúc với chân \(XY\) như hình 7 để bắt đầu nạp tụ, đồng thời khởi động đồng hồ đếm giây. Kim am-pe kế sẽ bị đẩy lên một mức cực đại do quán tính, ngay sau đó sẽ giật lại về một vị trí ban đầu ổn định: đó chính là dòng \(I\) cần ghi lại tại \(t=0\).

Cứ sau 20 giây ghi lại cường độ dòng điện.

Xả tụ

Việc xả tụ tiến hành ngay sau thí nghiệm nạp tụ tại phần trên, khi tụ đang có một điện tích \(q_0\) ban đầu nhất định. Trước khi xả tụ, đưa hai chân cầu dao \(AB\) về giữa không tiếp xúc. Đảo chiều hai đầu đo của am-pe kế để dòng xả có thể di chuyển ngược chiều kim đồng hồ.

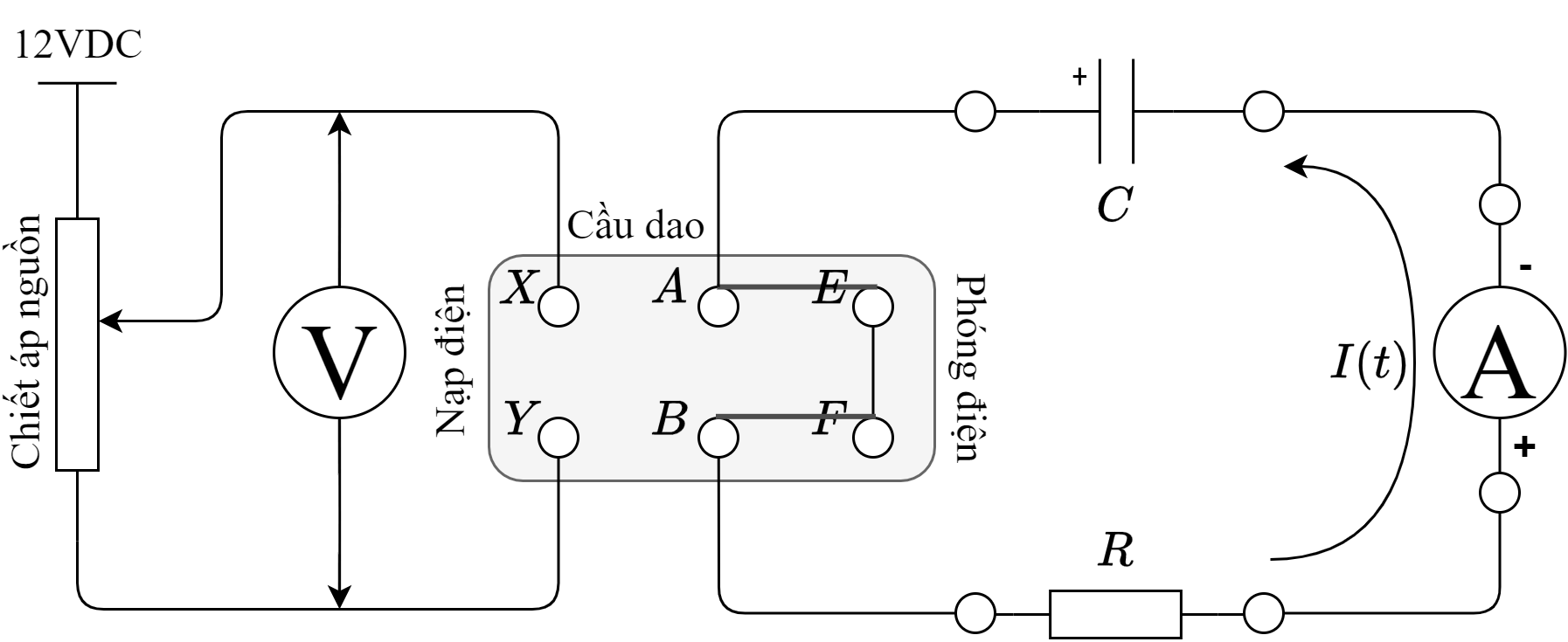
Đưa hai chân \(AB\) của cầu dao tiếp xúc với chân \(EF\) như hình 8 để bắt đầu xả tụ, đồng thời khởi động đồng hồ đếm giây. Kim am-pe kế sẽ bị đẩy lên một mức cực đại do quán tính, ngay sau đó sẽ lùi về một vị trí ban đầu ổn định: đó chính là dòng \(I\) cần ghi lại tại \(t=0\).

Cứ sau 20 giây ghi lại cường độ dòng điện vào bảng số liệu.

XỬ LÝ DỮ LIỆU

Hãy dựng đồ thị thể hiện sự phụ thuộc của dòng điện \(I\) theo thời gian \(t\). Theo lý thuyết, hàm \(I(t)\) có dạng hàm mũ \(\eqref{eq:2}\) và \(\eqref{eq:4}\):

\[I(t)=I_0\exp\left(-\frac{t}{RC}\right),\]

Do vậy hãy khớp đồ thị bằng một hàm mũ có dạng \(y=a\mathrm{e}^{bx}\). Từ hệ số \(b\) hãy suy ra hằng số thời gian \(\tau=\frac{1}{b}\) và so sánh với lý thuyết \(\tau=RC\).

Theo một cách trực quan khác, có thể lấy loga hai vế của hàm \(I(t)\):

\[\ln{I}=-\frac{1}{RC}t+\ln{I_0}.\]

Như vậy, ta có thể dựng đồ thị sự phụ thuộc của \(\ln{I}\) theo thời gian \(t\) và khớp hàm. Đồ thị thu được sẽ có dạng đường thẳng \(y=ax+b\), với hệ số \(a<0\). Từ hệ số này cũng có thể suy ra được hằng số thời gian \(\tau=-1/a\).