Bài 28C: Đo điện trở bằng mạch cầu Wheatstone

MỤC ĐÍCH

Nghiên cứu những quy luật của dòng điện trong mạch cầu Wheatstone, sử dụng nguyên lý của mạch cầu để xác định điện trở với độ chính xác cao.

NGUYÊN LÝ PHÉP ĐO

Mạch cầu Wheatstone có sơ đồ nguyên lý như hình 1. Điện trở cần đo \(R_x\) mắc nối tiếp với biến trở \(R\) – có chức năng làm tham chiếu. Bên nhánh song song còn lại, một dây ni-crôm có điện trở suất cao được chia thành hai phần có điện trở lần lượt bằng \(R_1\) và \(R_2\). Giá trị của \(R_1\) và \(R_2\) tỉ lệ với chiều dài mỗi đoạn, do vị trí của đầu đo của điện kế \(G\) quyết định.

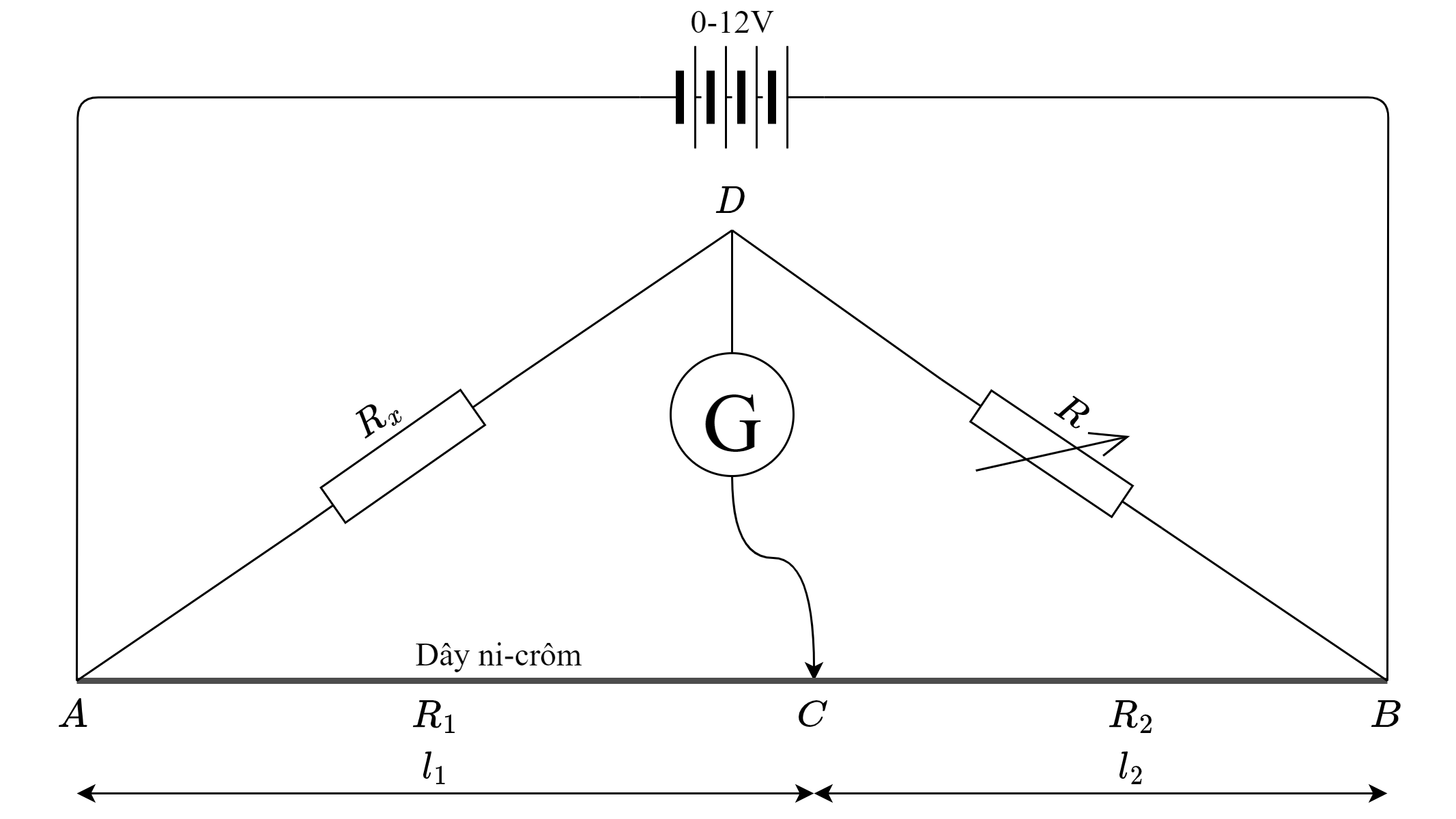
Nhìn chung sẽ có một dòng điện chạy từ nhánh bên này sang nhánh bên kia, đi xuyên qua điện kế và làm kim điện kế lệch 0. Nhưng hãy xét một tình huống đặc biệt: kim điện kế chỉ thăng bằng mức 0, không còn dòng điện chạy qua điện kế. Điều kiện để xảy ra tình huống trên là điện thế giữa hai nút \(C\) và \(D\) phải cân bằng: \(U_{CD}=0\). Điều này dẫn đến: \(U_{AC}=U_{AD}\), hay:

\[I_1R_1=I_xR_x.\]

Tương tự ta cũng có:

\[I_2R_2=I_RR.\]

Do không còn dòng qua điện kế \(G\) nên các dòng \(I_1\) và \(I_2\) qua dây ni-crôm được bảo toàn. Tương tự dòng \(I_x\) cũng chảy nguyên vẹn thành dòng \(I_R\) bên nhánh còn lại:

\[I_1=I_2,\quad I_x=I_R.\]

Từ những điều trên ta có thể thu về tỉ lệ:

\[\frac{R_x}{R}=\frac{R_1}{R_2}.\]

Dây ni-crôm đồng chất tiết diện đều nên các điện trở tỉ lệ với chiều dài mỗi đoạn: \(R_1/R_2=l_1/l_2\). Cuối cùng ta có được phép tìm điện trở theo tỉ lệ:

\[\frac{R_x}{R}=\frac{l_1}{l_2}.\tag{1}\]

QUY TRÌNH THÍ NGHIỆM

Sinh viên nhận 2 con trở \(R_x\) chưa biết giá trị để khảo sát. Với mỗi con trở như thế cần chuẩn bị 3 bảng dữ liệu như bên dưới. Mỗi bảng khảo sát tương ứng với một giá trị biến trở \(R\) do giáo viên chỉ định.

\[ \text{\(R=\ldots\)}\\ \begin{array}{c|c|c} \hline \text{Lần đo} & \text{\(l_1\) (cm)} & \text{\(l_2\) (cm)} \\ \hline \text{1} & & \\ \hline \text{2} & & \\ \hline \text{3} & & \\ \hline \text{4} & & \\ \hline \text{5} & & \\ \hline \text{Trung bình} & \text{\(\overline{l_1}=\ldots\)} & \text{\(\overline{l_2}=\ldots\)} \\ \end{array}\\ \text{\(\overline{R_x}=\ldots\)} \]

Đặt con trở \(R_x\) cần đo vào đúng vị trí trên mạch. Đưa chiết áp nguồn về giá trị khoảng dưới 5V và bật nguồn. Đưa biến trở \(R\) về giá trị thích hợp.

Di chuyển đầu đo \(C\) của điện kế \(G\) đến vị trí sao cho dòng điện qua điện kế chỉ về 0. Ghi lại các chiều dài \(l_1\) và \(l_2\) trên thước vào bảng dữ liệu.

Kéo lệch đầu đo sang phải hoặc trái, quan sát điện kế và lại đưa đầu đo về vị trí 0 lần nữa. Ghi lại \(l_1\) và \(l_2\) vào bảng. Cứ thế lặp lại phép đo 5 lần.

Đưa biến trở \(R\) sang giá trị tiếp theo và lặp lại hoàn toàn quy trình nói trên.

XỬ LÝ DỮ LIỆU

Với mỗi bảng dữ liệu, ta cần tính chiều dài trung bình \(\overline{l_1}\) và \(\overline{l_2}\). Dựa vào công thức (1) để tính điện trở cần đo:

\[\overline{R_x}=R\cdot\frac{\overline{l_1}}{\overline{l_2}}.\]

Tính các sai số phép đo và viết kết quả đầy đủ.