Bài 35A: Nghiệm lại các định luật cơ bản của quang hình học

MỤC ĐÍCH

Trong thí nghiệm này chúng ta tiến hành xác định chiết suất của một môi trường đồng nhất. Qua đó, người học sẽ cảm nhận được các quy luật về truyền thẳng, phản xạ và khúc xạ của ánh sáng.

ĐỊNH LUẬT CƠ BẢN

Quang hình học là lĩnh vực nghiên cứu về ánh sáng, theo đó ánh sáng lan truyền theo từng chùm tia, tương tác với môi trường theo những quy luật nhất định mà ta gọi là các định luật của quang hình học. Có bốn định luật quang hình học gồm:

Định luật về truyền thẳng. Trong một môi trường là đồng nhất, tia sáng lan truyền theo đường thẳng.

Định luật về tác dụng độc lập. Tác dụng của chùm sáng này không phụ thuộc vào sự có mặt của chùm sáng khác. Các tia sáng khi giao cắt nhau sẽ tiếp tục lan truyền tiếp theo hướng ban đầu mà không tương tác với nhau.

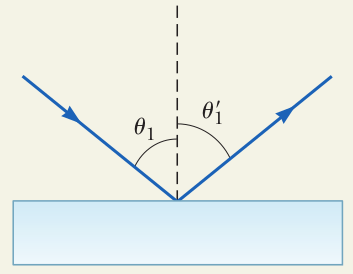
Định luật về phản xạ. Khi tia sáng đi đến bề mặt phân cách giữa hai môi trường khác nhau, sẽ xuất hiện tia phản xạ theo hướng sao cho góc phản xạ bằng góc tới:

\[\vartheta_1=\vartheta_2.\tag{1}\]

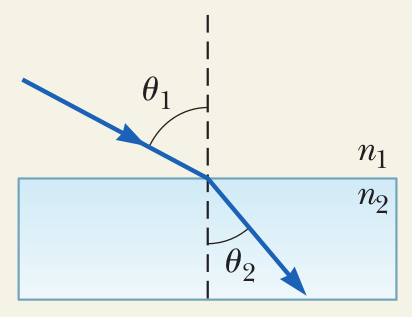
Định luật về khúc xạ. Khi gặp phải bề mặt phân cách giữa hai môi trường khác nhau, tia sáng có thể truyền qua môi trường bên kia và lệch khỏi hướng lan truyền ban đầu theo công thức Snell:

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=\frac{v_1}{v_2}.\tag{2}\]

trong đó \(\vartheta_1,\vartheta_2\) lần lượt là góc tới và góc khúc xạ, còn \(v_1,v_2\) là tốc độ lan truyền ánh sáng trong các môi trường tương ứng.

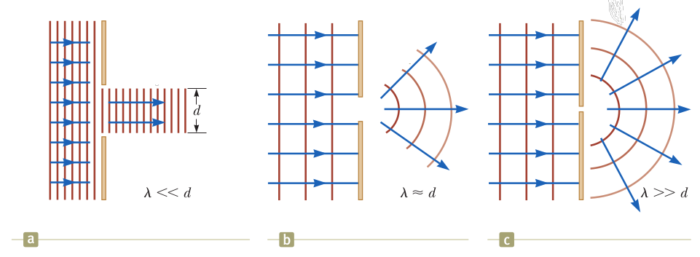
Các định luật quang hình học chỉ có thể áp dụng trong điều kiện bước sóng ánh sáng bé hơn nhiều so với kích thước các vật cản: \(\lambda<<d\). Khi hai tham số trên cùng bậc với nhau, \(\lambda\approx d\), ánh sáng không còn truyền thẳng nữa mà bị bẻ cong dù vẫn lan truyền trong một môi trường. Trường hợp bước sóng quá dài so với kích thước vật cản như ví dụ hình 5c, chùm sáng bị biến thành nguồn điểm.

CHIẾT SUẤT VÀ NGUYÊN LÝ FERMAT

Chiết suất của một môi trường thể hiện mối liên quan giữa tốc độ lan truyền của ánh sáng trong môi trường đó:

\[n=\frac{\text{Tốc độ ánh sáng trong chân không}}{\text{Tốc độ ánh sáng trong môi trường}}=\frac{c}{v}.\]

Chiết suất càng lớn, tốc độ lan truyền của ánh sáng càng chậm.

Các định luật quang hình học có thể giải thích theo nguyên lý Fermat: Giữa hai điểm cho trước, ánh sáng sẽ lan truyền từ điểm này đến điểm kia theo con đường tốn ít thời gian nhất có thể. Thời gian lan truyền phụ thuộc vào đường đi của tia sáng cũng như tốc độ lan truyền trong các môi trường. Do vậy có thể nói, chiết suất quyết định đến hình dạng của tia sáng khi nó lan truyền qua nhiều môi trường khác nhau.

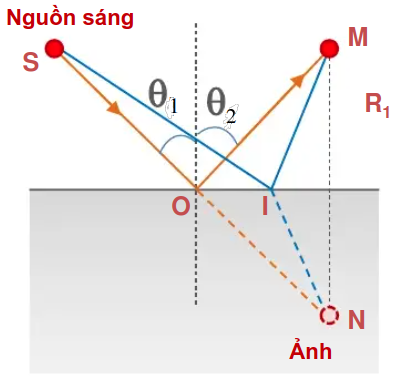
Định luật về phản xạ ánh sáng giải thích theo nguyên lý Fermat như sơ đồ hình 6. Trong các phản xạ khả dĩ, chỉ có phản xạ tại điểm \(O\), khi góc tới \(\vartheta_1\) bằng góc phản xạ \(\vartheta_2\), mới cho thời gian lan truyền nhanh nhất.

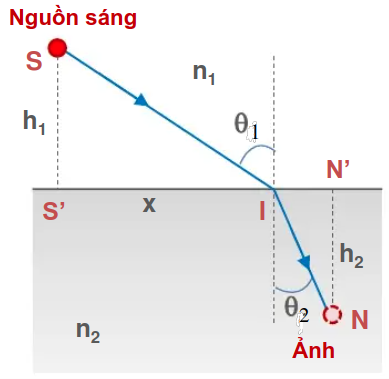
Định luật về khúc xạ ánh sáng giải thích theo nguyên lý Fermat như sơ đồ hình 7. Cho rằng tia sáng bị khúc xạ tại \(I\) trên mặt phân cách. Thời gian ánh sáng lan truyền theo đường đi \(SIN\):

\[t=\frac{SI}{v_1}+\frac{IN}{v_2}=\frac{\sqrt{x^2+h_1^2}}{v_1}+\frac{\sqrt{(S’N’-x)^2+h_1^2}}{v_2},\]

trong đó \(v_1,v_2\) lần lượt là tốc độ lan truyền trong mỗi môi trường. Vị trí điểm \(I\) cần thỏa mãn điều kiện cực tiểu của thời gian:

\[\frac{dt}{dx}=\frac{1}{v_1}\cdot\frac{x}{\sqrt{x^2+h_1^2}}-\frac{1}{v_2}\cdot\frac{S’N’-x}{\sqrt{x^2+h_1^2}}=0.\]

Từ đây thu được phương trình của định luật khúc xạ ánh sáng:

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=\frac{v_1}{v_2}.\]

Biểu diễn tốc độ ánh sáng trong môi trường thông qua chiết suất:

\[v_1=\frac{c}{n_1},\quad v_2=\frac{c}{n_2},\]

ta có thể viết lại định luật khúc xạ dưới dạng:

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=\frac{n_2}{n_1}.\tag{2′}\]

Phương trình (2′) cho phép chúng ta xác định được chiết suất của các môi trường thông qua góc tới và góc phản xạ. Việc xác định chiết suất thuận tiện hơn nhiều so với trực tiếp xác định tốc độ của ánh sáng trong môi trường.

PHẢN XẠ TOÀN PHẦN

Khi một tia sáng lan truyền từ môi trường này sang môi trường khác, tia phản xạ và tia khúc xạ thường xuất hiện đồng thời, phân tách năng lượng của tia ban đầu ra hai phía của mặt phân cách. Xét một tia sáng đi từ môi trường có chiết suất cao sang môi trường chiết suất thấp hơn: \(n_1>n_2\).

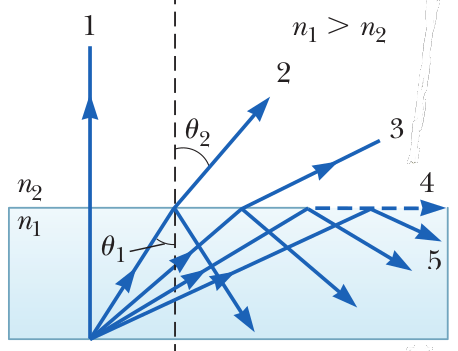
Theo định luật khúc xạ (2′):

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=\frac{n_2}{n_1},\]

góc khúc xạ \(\vartheta_2\) phải lớn hơn góc tới \(\vartheta_1\). Quan sát theo hình 8, khi góc tới tăng dần, góc khúc xạ cũng tăng theo và đạt ngưỡng \(90^\circ\) trước (tia 4). Khi góc tới tiếp tục tăng, góc khúc xạ sẽ biến mất. Lúc này chỉ còn tia phản xạ, mang toàn bộ năng lượng của tia tới ban đầu. Ta nói rằng tia sáng bị phản xạ toàn phần.

Góc tới hạn \(\vartheta_c\), khi hiện tượng phản xạ toàn phần bắt đầu xảy ra tính theo công thức:

\[\sin\vartheta_c=\frac{n_2}{n_1}.\tag{3}\]

NGUYÊN LÝ PHÉP ĐO

Thí nghiệm khảo sát định luật phản xạ và định luật khúc xạ mô tả như hình dưới. Môi trường khảo sát có thể là chất rắn hoặc lỏng. Nếu là chất rắn, nó được đúc thành khối hình bán nguyệt. Còn nếu là chất lỏng, nó được chứa chứa trong bình hình bán nguyệt.

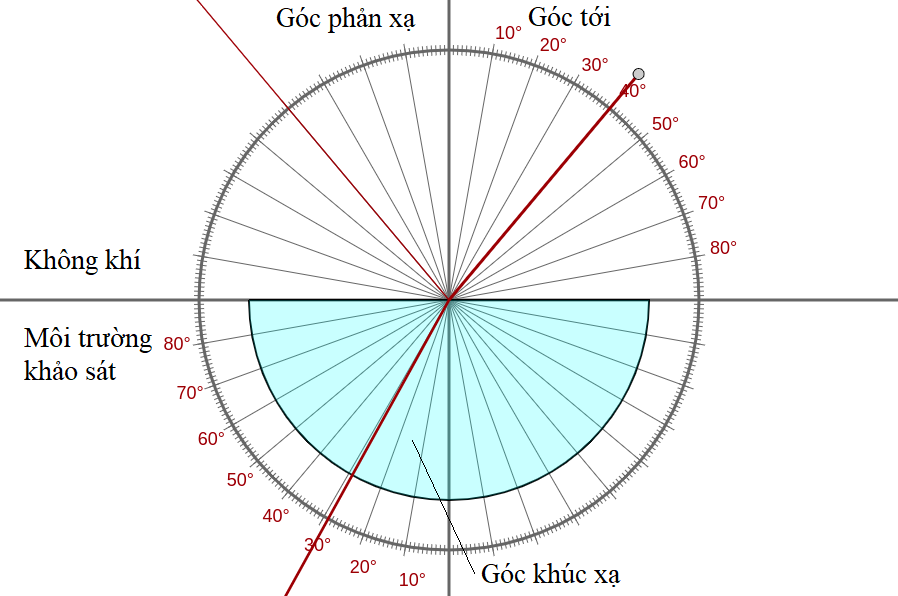
Bài thí nghiệm chia thành hai phần. Phần 1 khảo sát tia sáng đi từ không khí vào môi trường, phần 2 tia sáng lại đi từ môi trường ra không khí.

Với phần 1, một tia sáng chiếu thẳng đến tâm của khối bán nguyệt. Lúc này sẽ xuất hiện tia phản xạ và tia khúc xạ. Tia khúc xạ khi ra khỏi môi trường khảo sát mà không bị bẻ cong do trùng phương pháp tuyến với bề mặt tròn. Từ đây góc phản xạ và khúc xạ dễ dàng xác định bằng thước góc.

Không khí có chiết suất \(n_1=1\), còn môi trường khảo sát có chiết suất \(n_2=n\). Thông qua định luật khúc xạ (2′), ta có thể xác định chiết suất của chất khảo sát.

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=n.\]

[Hình 10]

Tại phần 2, tia sáng được chiếu theo hướng ngược lại, đâm thẳng góc vào bề mặt tròn của khối bán nguyệt, đi thẳng vào tâm hệ khảo sát. Lúc này tia phản xạ xuất hiện bên trong môi trường khảo sát. Còn tia khúc xạ sẽ ló ra ngoài không khí. Đặc biệt tại phần 2 này, ta sẽ quan sát được hiện tượng phản xạ toàn phần và góc tới hạn.

Tia tới đi từ môi trường khảo sát có chiết suất \(n_1=n\), khúc xạ ra ngoài không khí có chiết suất \(n_2=1\). Theo định luật khúc xạ (2′), ta có thể xác định chiết suất của chất khảo sát:

\[\frac{\sin\vartheta_1}{\sin\vartheta_2}=\frac{1}{n}.\]

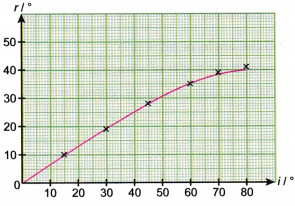
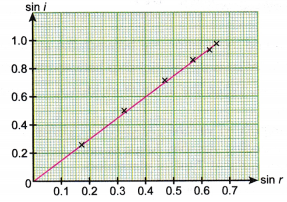
Mối quan hệ giữa góc khúc xạ và góc tới thể hiện qua đồ thị như hình 11. Tuy vậy, quy luật chỉ xuất hiện khi ta dựng đồ thị của sin các góc ấy. Sự phụ thuộc tuyến tính giữa hai đại lượng này thể hiện rõ như hình 12.

QUY TRÌNH THÍ NGHIỆM

Sinh viên tiếp nhận chất làm thí nghiệm từ giáo viên.

Phần 1: Tia sáng từ không khí vào môi trường khảo sát

Đặt khối bán nguyệt vào tâm của hệ đo góc như hình 9. Góc \(0^\circ\) trùng với pháp tuyến.

Bật đèn ở chế độ phát ra 1 tia sáng. Ta bắt đầu tiến hành thí nghiệm với giá trị góc tới \(\vartheta_1=0^\circ–85^\circ\), cách nhau mỗi \(5^\circ\). Với mỗi góc tới \(\vartheta_1\) như thế, ta chiếu tia sáng thẳng vào tâm hệ khảo sát, ghi lại các góc phản xạ và khúc xạ tương ứng vào bảng 1.

Bảng 1: Dữ liệu phần 1

\[ \begin{array}{c|c|c|c|c} \hline \text{Góc tới} & \text{Góc phản xạ} & \text{Góc khúc xạ} & \text{\(\sin\vartheta_1\)} & \text{\(\sin\vartheta_2\)} \\ \text{\(\vartheta_1\)} & \text{\(\vartheta_1’\)} & \text{\(\vartheta_2\)} & &\\ \hline \text{\(0^\circ\)} & & & & \\ \hline \text{\(5^\circ\)} & & & &\\ \hline \text{\(10^\circ\)} & & & & \\ \hline … & & \\ \hline \end{array}\\ \]

Phần 2: Tia sáng từ môi trường khảo sát ra không khí

Đặt khối bán nguyệt vào tâm của hệ đo góc như hình 10. Góc \(0^\circ\) trùng với pháp tuyến.

Bật đèn ở chế độ phát ra 1 tia sáng. Ta bắt đầu tiến hành thí nghiệm với giá trị góc tới \(\vartheta_1=0^\circ–85^\circ\), cách nhau mỗi \(5^\circ\). Với mỗi góc tới \(\vartheta_1\) như thế, ta chiếu tia sáng thẳng vào tâm hệ khảo sát, ghi lại các góc phản xạ và khúc xạ tương ứng vào bảng 2.

Lưu ý rằng ở phần 2 này có thể tia khúc xạ sẽ không xuất hiện với những góc tới nhất định. Trường hợp như vậy cần để trống. Hãy dò tìm góc tới hạn \(\vartheta_c\), khi tia khúc xạ bắt đầu bị biến mất, ghi vào bảng 2.

Bảng 2: Dữ liệu phần 2

\[ \begin{array}{c|c|c|c|c} \hline \text{Góc tới} & \text{Góc phản xạ} & \text{Góc khúc xạ} & \text{\(\sin\vartheta_1\)} & \text{\(\sin\vartheta_2\)} \\ \text{\(\vartheta_1\)} & \text{\(\vartheta_1’\)} & \text{\(\vartheta_2\)} & &\\ \hline \text{\(0^\circ\)} & & & & \\ \hline \text{\(5^\circ\)} & & & &\\ \hline \text{\(10^\circ\)} & & & & \\ \hline … & & \\ \hline \end{array}\\ \text{Góc tới hạn: \(\vartheta_c=\ldots\)} \]

XỬ LÝ DỮ LIỆU

Từ các bảng dữ liệu, vẽ đồ thị sự phụ thuộc của góc khúc xạ \(\vartheta_2\) vào góc tới \(\vartheta_1\). Vẽ đồ thị sự phụ thuộc của \(\sin\vartheta_2\) vào \(\sin\vartheta_1\).

Từ đồ thị liên hệ giữa \(\sin\vartheta_1\) và \(\sin\vartheta_2\), khớp hàm bằng đường thẳng và tìm hệ số góc để suy ra chiết suất \(n\) của môi trường khảo sát.

Dựa vào góc tới hạn \(\vartheta_c\) của hiện tượng phản xạ toàn phần, tính chiết suất theo công thức (3):

\[n=\frac{1}{\sin\vartheta_c}.\]

So sánh các giá trị chiết suất thu được theo các phần thí nghiệm. Tính tốc độ của ánh sáng trong môi trường khảo sát.

Dựa vào thực nghiệm trên, miêu tả tính chất của tia phản xạ và tia khúc xạ khi tia tới đi đến mặt phân cách giữa hai môi trường.