Có lẽ trong chúng ta, khi đọc bài này, hầu như ai cũng từng học qua số phức. Và cũng có lẽ số phức phần nào để lại những bí ẩn khó hiểu. Bài viết này ra đời với mong muốn góp phần làm sáng tỏ vấn đề số phức, giúp sinh viên các ngành kĩ thuật vận dụng tốt hơn, thấu hiểu hơn về bản chất của các biểu diễn phức.
\(j\) – “đơn vị ảo”
Số phức theo định nghĩa thông thường được biểu diễn dưới dạng \(z = a+jb\) gồm hai thành phần: phần thực \(a\) và phần ảo \(b\). “Phức” ở đây có nghĩa là sự pha trộn giữa “thực” và “ảo”. \(j\) được gọi là “đơn vị ảo” và có tính chất vô cùng độc đáo:
\[j^2 = -1.\]
Và mọi chuyện trở nên khó hiểu từ đó. Suy nghĩ thông thường của chúng ta đấu tranh rằng, số gì bình phương lên lại bằng \(-1\), một số âm. Lẽ ra bình phương một số bất kì phải ra số dương chứ! Chúng ta đã chấp nhận nó như một tiên đề. Số phức đi vào tâm tưởng sinh viên như một kẻ nhiễu loạn, phá phách.
Số phức trong toán học thuần tuý được xây dựng hết sức công phu, chặt chẽ và sâu sắc. Ở đây chúng ta chỉ bàn đến một vài khía cạnh thường xuất hiện trong kỹ thuật: chuyển động quay.
\(j\) – toán tử quay
Trong bài viết này chúng ta có thể tiếp cận số phức theo hướng hình học, giúp các ứng dụng kĩ thuật có cái nhìn dễ hình dung hơn. Hãy bắt đầu từ ý nghĩa hình học của kí hiệu \(j\) và xem như một tiên đề:
\(j\) là toán tử “quay 90 độ”
Cho vector \((1,0)\), tức số \(1\) trên trục hoành, quay một góc \(90^\circ\) bằng toán tử \(j\), ta viết \(j1\), và thu được vector \((0,1)\), chính là số \(1\) trên trục tung. Giả sử cho toán tử \(j\) tác dụng hai lần lên số \(1\), tức \(j^21\), bằng cách quay vector \((1,0)\) theo góc \(90^\circ\) hai lần, chúng ta thu được vector \((-1,0)\), tức số \(-1\) trên trục hoành. Đó là lý do tại sao \(j^2\) lại bằng \(-1\).
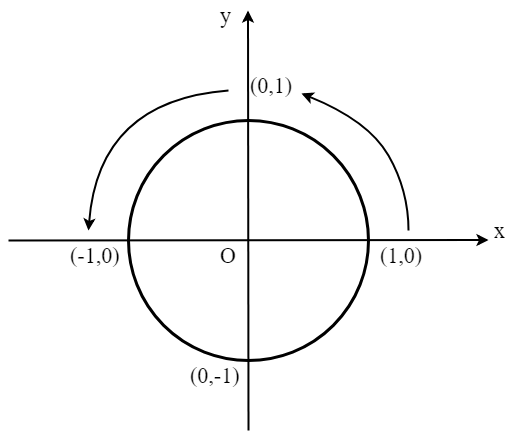
Bản chất của \(j\) không khác gì chính là phép quay quanh một trục. Nếu muốn quay một góc bất kì, ví dụ \(30^\circ\), ta đưa \(30/90 = 1/3\) vào tầm tác dụng của toán tử \(j\) và thu được \(j^{1/3}\) – chính là phép quay \(30\) độ. Để kiểm tra lại, ta làm phép quay \(30^\circ\) ba lần:
\[\left(j^{1/3}\right)^3=j,\]
cho ra đúng phép quay \(90\) độ, phù hợp logic.
Từ đây khi biểu diễn vector \(z = a+jb\), ta hiểu rằng vector này được cấu thành từ hai thành phần hình chiếu: thành phần \(a\) theo trục hoành, còn thành phần \(b\) bị quay \(90\) độ và hướng theo trục tung. Toán tử \(j\) phải là phép quay \(90\) độ chứ không phải góc nào khác, bởi vì có như thế ta mới làm việc với hệ trực giao (cắt nhau vuông góc), rất thuận tiện khi tính toán. Giả như \(j\) là phép quay \(60\) độ, ta vẫn biểu diễn được mọi số, nhưng các thành phần vector không phải trực giao nên các định lý sẽ có dạng phức tạp không cần thiết, đôi khi không thể biểu diễn. Điển hình như định lý Pythagor không thể biểu diễn một cách đơn giản \(r^2 = a^2+b^2\) như hệ trực giao (\(r\) – chiều dài của vector \(z\)).
Toán tử \(j\) và chuyển động tròn đều
Xét một chất điểm chuyển động tròn đều với vận tốc góc \(\omega\) theo ngược chiều kim đồng hồ trên quỹ đạo tròn có tâm ở gốc toạ độ và bán kính \(R\) như hình dưới.
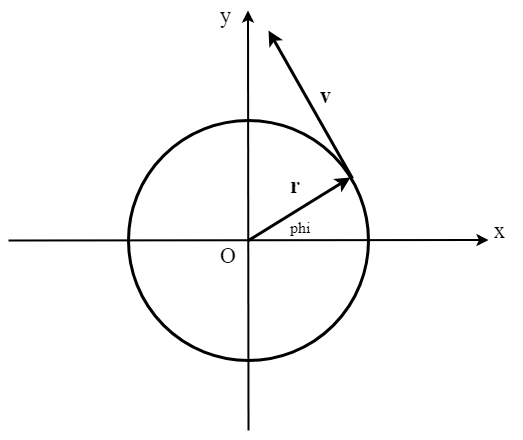
Ta có thể biểu diễn toạ độ của chất điểm theo hệ trục toạ độ Descartes:
\begin{eqnarray}
x&=&R\cos\omega t,\nonumber\\
y&=&R\sin\omega t,\nonumber
\end{eqnarray}
hay
\begin{eqnarray}
\vec{r}&=&x+jy\nonumber\\
&=&R\cos\omega t+jR\sin\omega t.\tag{1}
\label{eq:1a}
\end{eqnarray}
Từ môn động học chất điểm, ta biết rằng vận tốc dài của vật chuyển động tròn đều là vector có độ lớn \(v=\omega|\vec{r}|\) và hướng vuông góc với bán kính quỹ đạo như hình vẽ. Sử dụng toán tử quay \(90^\circ\), hay toán tử \(j\), ta có thể biểu diễn mối liên hệ giữa vận tốc dài và vận tốc góc:
\[\vec{v}=j\omega\vec{r}.\]
Bởi vận tốc là đạo hàm của toạ độ theo thời gian:
\begin{equation}
\frac{d\vec{r}}{dt}=j\omega\vec{r}.\tag{2}
\label{eq:1}
\end{equation}
Phương trình \(\eqref{eq:1}\) có nghiệm là hàm mũ:
\begin{equation}
\vec{r}=Re^{j\omega t},\tag{3}
\label{eq:2}
\end{equation}
miêu tả chuyển động tròn đều dưới dạng số phức.
So sánh \(\eqref{eq:1a}\) và \(\eqref{eq:2}\), ta rút ra được hệ thức:
\begin{equation}
e^{j\varphi}=\cos\varphi+j\sin\varphi,\tag{4}
\label{eq:3}
\end{equation}
trong đó \(\varphi=\omega t\). Hệ thức \(\eqref{eq:3}\) còn gọi là công thức Euler, vừa được chứng minh bằng phương pháp hình học. Nếu thay \(\varphi=\pi\) ta có được đẳng thức Euler nổi tiếng
\[e^{j\pi}+1=0,\]
có tính chất hết sức đặc biệt: nó chứa số \(0\), đơn vị số thực \(1\), đơn vị “số ảo” \(j\), số \(\pi\), số \(e\) và dấu đẳng thức.
Công thức \(\eqref{eq:2}\) cho chúng ta một công cụ biểu diễn số phức theo một cách thuận tiện khác:
\[z=Re^{j\varphi},\]
với \(R\) – độ dài của vector \(z\), \(\varphi\) – góc hợp bởi vector \(z\) với trục \(Ox\).
Lưu ý rằng bản thân toán tử \(j\) cũng có thể biểu diễn thành hàm mũ với góc quay \(\varphi=\pi/2\):
\[j=e^{j\dfrac{\pi}{2}}.\]
\(j\) – toán tử tuyến tính
Phép quay \(j\) là một toán tử tuyến tính, có nghĩa nó mang đầy đủ các tính chất kết hợp và tính chất phân phối. Thực vậy, việc kéo dài vector \(z\) lên \(k\) lần rồi cho quay một góc \(90\) độ cũng tương đương với việc cho vector \(z\) quay \(90\) độ trước rồi sau đó mới kéo giãn ra \(k\) lần:
\[j(kz)=k(jz).\]
Mặt khác, việc cho hai vector cộng lại rồi cho vector tổng quay \(90\) độ cũng cho ra cùng một kết quả với việc cho mỗi vector quay riêng rẽ \(90\) độ rồi mới cộng chúng lại với nhau:
\[j(z_1+z_2)=jz_1+jz_2.\]
Do mang bản chất tuyến tính, toán tử \(j\) hành xử không khác gì một phép nhân. Cho nên trong các tình huống bắt gặp số phức, ta thấy \(j\) như một thành tố được nhân vào mà ta hay quen gọi một cách không có lợi là “đơn vị ảo”. Chúng ta cùng kiểm tra lại toán tử quay \(90\) độ \(j\) khi nó tác dụng lên vector \(z=a+jb\):
\[jz=j(a+jb)=-b+ja=z’.\]
Rõ ràng toán tử \(j\) đã quay vector \(z\) thành \(z’\), một vector có cùng độ dài nhưng lệch một góc \(90\) độ theo ngược chiều kim đồng hồ. Ta cũng thấy rõ điều đó khi biểu diễn tác dụng này theo hàm mũ:
\[jz=jRe^{j\varphi}=Re^{j(\varphi+\pi/2)}.\]
Nhờ tính chất tuyến tính, ta thấy phép cộng trừ hai số phức không khác gì cộng trừ hai vector:
\[(a_1+jb_1)\pm(a_2+jb_2)=(a_1\pm a_2)+j(b_1\pm b_2).\]
Trong khi đó phép nhân hai số phức chính là sự chồng chập của phép quay:
\[z_1z_2 = R_1e^{j\varphi_1}R_2e^{j\varphi_2}=R_1R_2e^{j(\varphi_1+\varphi_2)},\]
có nghĩa: tích của hai số phức có modul bằng tích các modul và có góc quay bằng tổng các góc quay. Từ đây có thể khái quát lên phép tính luỹ thừa cho số phức, theo De Moivre:
\[z^n=\left(Re^{j\varphi}\right)^n=R^ne^{jn\varphi},\]
cũng như phép khai căn:
\[z^{1/n}=\left(Re^{j\varphi}\right)^{1/n}=R^{1/n}e^{j\varphi/n}.\]
Phép khai căn của số phức mang lại vẻ đẹp thuận tiện về tính đối xứng. Căn bậc hai luôn có \(2\) nghiệm, căn bậc \(3\) luôn có \(3\) nghiệm, căn bậc \(n\) luôn có \(n\) nghiệm… Ví dụ ta muốn lấy căn bậc hai của \(4\), tức căn của vector \((4,0)\), chỉ cần chia quỹ đạo quay của vector thành \(2\) nửa, một nghiệm sẽ cho vector \((2,0)\) tức số \(2\), còn nghiệm kia cho ra vector \((-2,0)\) tức \(-2\).
Thử lại, xét theo vector, \((2,0)\) khi bình phương lên sẽ cho ra vector \((4,0)\), vì góc quay của nó vốn bằng \(0\), quay thêm lần nữa cũng trùng hướng đó. Vector \((-2,0)\) khi bình phương lên cũng vẫn cho ra vector \((4,0)\), bởi vì \((-2,0)\) có hướng \(180\) độ, bình phương lên sẽ thành \(360^\circ\), tức \(0\) độ. Nếu thử lại theo thành phần trục hoành, ta vẫn có được \(2^2 = 4\) và \((-2)^2 = 4\).
Nhớ lại rằng trong toán học thông thường, căn bậc hai của \(4\) chỉ bằng \(2\), trong khi đó theo định nghĩa căn của \(4\) phải là số nào đó bình phương lên bằng \(4\), lúc này cả \(2\) lẫn \(-2\) đều thoả mãn. Hai nghiệm dành cho căn bậc hai là kết quả hợp lý.
Moment quay của một vector
Xét hai số phức
\begin{eqnarray}
z_1&=&a_1+jb_1,\nonumber\\
z_2&=&a_2+jb_2.\nonumber
\end{eqnarray}
Phép nhân liên hợp của hai số phức \(z_1\) và \(z_2\) được định nghĩa như sau:
\begin{eqnarray}
z_1^*z_2&=&(a_1-jb_1)(a_2+jb_2)\nonumber\\
&=&(a_1a_2+b_1b_2)+j(a_1b_2-b_1a_2),\tag{5}
\label{eq:nhanlienhop}
\end{eqnarray}
trong đó \(z_1^*=a_1-jb_1\) – số phức liên hợp của \(z_1\). Phần thực của phép nhân liên hợp \(\eqref{eq:nhanlienhop}\) được gọi là tích vô hướng của hai vector:
\begin{equation}
z_1\cdot z_2=\Re(z_1^*z_2)=a_1a_2+b_1b_2.
\end{equation}
Phần “ảo” của phép nhân liên hợp \(\eqref{eq:nhanlienhop}\) có trị số bằng độ lớn của vector tích có hướng:
\begin{equation}
|z_1\times z_2|=\Im(z_1^*z_2)=a_1b_2-b_1a_2.
\end{equation}
Chiều của vector tích có hướng \(z_1\times z_2\) được quy ước theo trục vuông góc với mặt phẳng chứa \(z_1\) và \(z_2\) theo quy tắc xoắn ốc.
Xét vector \(\vec{F}\) nằm trên mặt phẳng \(xOy\) với các thành phần hình chiếu \(F_x\) và \(F_y\):
\[\vec{F}=F_x+jF_y.\]
Moment của vector \(\vec{F}\) là một vector hướng theo trục \(Oz\), biểu diễn qua tích có hướng của cánh tay đòn \(\vec{r}\) và \(\vec{F}\):
\begin{equation}
|\vec{r}\times\vec{F}|=\Im(\vec{r}^*\vec{F})=xF_y-yF_x,\tag{6}
\label{eq:moment}
\end{equation}
trong đó \(\vec{r}=x+jy\) – toạ độ của điểm đặt vector \(\vec{F}\). Nếu \(\vec{F}\) là lực tác dụng, công thức \(\eqref{eq:moment}\) miêu tả moment lực, nếu \(\vec{F}\) là động lượng, công thức \(\eqref{eq:moment}\) miêu tả moment động lượng… Trong vật lý, moment của một vector gắn liền với vận động quay, do đó sự có mặt của toán tử \(j\) không có gì lạ.
Toán tử \(j\) trong dao động và sóng
Trong lĩnh vực dao động và sóng, bao gồm cả dòng điện xoay chiều cũng như xử lý tín hiệu, toán tử \(j\) được áp dụng rất thành công nhờ quy sự dao động điều hoà thành hình chiếu của một chuyển động tròn. Không có gì khó hiểu khi trong các lĩnh vực này, số phức được áp dụng rộng rãi do tính chất quay của nó.
Trong khi đó mọi đại lượng vật lý đều phải là số thực, thì quả thật số phức không hề đưa vào một thành phần “ảo” nào ở đây cả. Số phức lúc này chẳng qua là một vector quay đều quay trục với vận tốc mà ta gọi là tần số. Làm việc với toán tử quay thuận tiện hơn nhiều so với các phép toán đầy sin, cos của lượng giác, bởi vì phép cộng vector đơn giản hơn nhiều so với phép cộng lượng giác.
Dòng điện biến thiên điều hoà có thể diễn tả thông qua hình chiếu của chuyển động tròn đều:
\[I=I_0\cos\omega t=\Re\left(I_0e^{j\omega t}\right).\]
Trong nhiều trường hợp, người ta quy luôn đại lượng biến thiên điều hoà tương đương với phép quay đều. Khi ấy dòng điện xoay chiều nói trên viết hẳn thành:
\[I=I_0e^{j\omega t}.\]
Khi dòng này đi qua điện trở thuần \(R\), nó tạo ra một điện áp theo định luật Ohm:
\[U_R=RI=RI_0e^{j\omega t}.\]
Khi dòng này tạo tác dụng tích điện lên tụ có điện dung \(C\):
\[I=\frac{dq}{dt}=C\frac{dU_C}{dt}\]
và tạo nên một điện áp tức thời giữa hai bản tụ:
\[U_C=\frac{1}{C}\int{I\,dt}=\frac{1}{j\omega C}I_0e^{j\omega t}=-j\frac{1}{\omega C}\cdot I.\]
Khi dòng \(I\) nói trên đi qua một ống dây có độ tự cảm \(L\), điện áp tức thời xuất hiện trên cuộn dây tuân theo định luật Faraday:
\[U_L=\frac{d\Phi}{dt}=L\frac{dI}{dt}=j\omega LI_0e^{j\omega t}=j\omega L\cdot I.\]
Từ trên ta thấy rằng, điện áp giữa hai đầu điện trở thuần luôn cùng pha với dòng điện. Với tụ, điện áp chậm pha hơn dòng điện \(1/4\) chu kỳ. Còn điện áp hai đầu cuộn cảm lại nhanh pha hơn dòng điện \(1/4\) chu kỳ.
Công suất tức thời là tích vô hướng của điện áp với cường độ dòng điện:
\[P=U\cdot I=\Re(U^*I),\]
trong đó \(U^*\) – số phức liên hợp của \(U\). Áp dụng lần lượt cho các trường hợp điện trở, tụ điện và cuộn cảm:
\[P_R=\Re(U_R^*I)=\Re(RI_0e^{-j\omega t}I_0e^{j\omega t})=I_0^2R.\]
\[P_C=\Re(U_C^*I)=\Re(\frac{1}{j\omega C}I_0e^{-j\omega t}I_0e^{j\omega t})=0.\]
\[P_L=\Re(U_L^*I)=\Re(j\omega LI_0e^{-j\omega t}I_0e^{j\omega t})=0.\]
Tụ điện và cuộn cảm lý tưởng không gây hao phí công suất trên chúng.
Toán tử \(j\) trong cơ học lượng tử
Phương trình Newton đóng vai trò trọng tâm trong cơ học cổ điển:
\[\frac{\partial^2 x}{\partial t^2}=\frac{F_x}{m}.\]
Theo đó, trạng thái (gồm toạ độ và vận tốc) của hạt trong tương lai rất gần \(t+dt\) phụ thuộc hoàn toàn vào trạng thái lúc thời điểm hiện tại \(t\). Biết trạng thái của hiện tại, có thể suy ra trạng thái của tương lai rất gần. Rồi trạng thái của tương lai rất gần sau đó cũng lại được suy ra từ trạng thái trước đó. Cứ thế, nhờ vào phương trình Newton, ta có thể suy ra trạng thái của hạt tại bất kì thời điểm nào trong tương lai.
Trong cơ học lượng tử, trạng thái của hạt được miêu tả qua hàm sóng \(\psi(x,t)\) luôn biến chuyển theo thời gian. Để tiên đoán trạng thái tương lai, ta cũng cần một phương trình cơ bản, tương tự như phương trình Newton trong cơ học cổ điển.
Theo Louis de Broglie, một hạt tự do có xung lượng \(p\) và năng lượng \(E\) xác định sẽ tương ứng với một sóng hình sin có số sóng \(k=p/\hbar\) và tần số \(\omega=E/\hbar\):
\begin{equation}
\psi(x,t)=A\cos(kx-\omega t),\tag{7}
\label{eq:hamsong1}
\end{equation}
với \(\hbar\) – hằng số Planck. Nói ngược lại một sóng vật chất hình sin có số sóng \(k\) và tần số \(\omega\) sẽ tương ứng với một hạt tự do có xung lượng và năng lượng:
\[p=\hbar k,\qquad E=\hbar\omega.\]
Mặt khác, giữa xung lượng và năng lượng lại có mối liên hệ:
\[E=\frac{p^2}{2m}\]
hay:
\begin{equation}
\hbar\omega=\frac{\hbar^2k^2}{2m}.\tag{8}
\label{eq:lienhe}
\end{equation}
Để làm xuất hiện những biểu thức trong \eqref{eq:lienhe}, chỉ cần lấy đạo hàm của hàm sóng \eqref{eq:hamsong1} theo thời gian và theo toạ độ:
\begin{eqnarray}
\hbar\frac{\partial\psi}{\partial t}&=&\hbar\omega\sin(kx-\omega t),\nonumber\\
-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}&=&\frac{\hbar^2k^2}{2m}\cos(kx-\omega t).\tag{9}
\label{eq:he1}
\end{eqnarray}
Hệ thức \eqref{eq:lienhe} sẽ được thoả mãn nếu trong hệ \eqref{eq:he1} hàm sin biến thành hàm cos:
\[\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}.\]
Thực tế ta có thể biến đổi hàm sin thành hàm cos thông qua phép dịch pha \(1/4\) chu kì, tức xoay pha lên \(90^\circ\):
\[\sin(\alpha+\pi/2)=\cos\alpha.\]
Từ đây ta có được phương trình:
\begin{equation}
\{\mathrm{xoay pha}\ 90^\circ\}\left(\hbar\frac{\partial\psi}{\partial t}\right)=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}.\tag{10}
\label{eq:schrodinger1}
\end{equation}
Tuy nhiên toán tử \(\{\mathrm{xoay pha}\ 90^\circ\}\) nói trên không thuận tiện trong biểu diễn và tính toán. Do đó trong cơ học lượng tử, người ta đề xuất sử dụng các hàm sóng dưới dạng phức. Trường hợp sóng sin tương ứng với hạt tự do hàm sóng \eqref{eq:hamsong1} viết thành:
\[\psi(x,t)=Ae^{j(kx-\omega t)}.\]
Khi ấy toán tử \(\{\mathrm{xoay pha}\ 90^\circ\}\) có thể thay bằng toán tử quay \(j\), và phương trình \eqref{eq:schrodinger1} được viết lại:
\begin{equation}
j\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}.
\label{eq:schrodinger2}
\end{equation}
Trong trường hợp tổng quát khi hạt chuyển động trong trường thế \(U(x)\):
\begin{equation}
j\hbar\frac{\partial\psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\psi}{\partial x^2}+U(x)\psi.\tag{11}
\label{eq:schrodinger}
\end{equation}
Phương trình \eqref{eq:schrodinger} do Schrodinger đề xuất vào năm 1926, đóng vai trò chủ đạo trong cơ học lượng tử. Với sóng sin cho hạt tự do, toán tử \(j\) đứng trước phương trình trên đơn giản chỉ là sự đảo pha với ý nghĩa rằng: trạng thái của hạt trong hiện tại có thể suy ra từ trạng thái của quá khứ \(1/4\) chu kì trước đó. Với hạt trong trường thế bất kì, tính thuần nhất của phương trình Schrodinger cho phép trạng thái của hạt là sự chồng chập từ những sóng sin, và sự đảo pha \(90^\circ\) vẫn mang ý nghĩa.
Toán tử \(j\) và các hệ đối xứng
Định lý Cauchy dành cho hàm số phức nói rằng: nếu hàm \(f(z)\) khả vi thì tích phân của hàm đó theo một đường cong khép kín bất kì luôn bằng \(0\):
\[\oint{f(z)\,dz}=0.\]
Cụm câu “theo một đường khép kín” đã nói lên bản chất vận động quay của vector. Định lý này tương đồng với định lý bảo toàn cơ năng trong vật lý: công của một trường lực xuyên tâm theo một đường cong khép kín bất kì luôn bằng 0. Thực vậy, trường lực xuyên tâm thoả mãn điều kiện khả vi Cauchy-Riemann:
\begin{eqnarray}
\frac{\partial F_x}{\partial x}&=&\frac{\partial F_y}{\partial y},\nonumber\\
\frac{\partial F_x}{\partial y}&=&-\frac{\partial F_y}{\partial x}.\nonumber
\end{eqnarray}
Cũng có nghĩa rằng, công của một trường lực xuyên tâm không phụ thuộc vào đường đi, chỉ phụ thuộc vào điểm đầu và điểm cuối. Do vậy ta nói trường vector xuyên tâm là một trường bảo toàn. Bảo toàn cơ năng là một định lý, không phải định luật vì được chứng minh hoàn toàn toán học. Chỉ có bảo toàn năng lượng mới gọi là định luật.
Phải nói rằng ở đâu có tính đối xứng tâm, đối xứng trục, hay tính tuần hoàn, ở đó có tính chất của hàm số phức. Các hàm số siêu việt xuất thân từ số phức như hàm Bessel, hàm Hankel, các hàm cầu… đều là hệ quả của tính chất quay của vector thông qua toán tử \(j\), cho nên Bessel, Hankel, hàm cầu… ứng dụng rộng rãi trong việc giải các bài toán dao động của màng tròn, truyền nhiệt của thanh trụ tròn, lý thuyết nguyên tử khi làm việc với các moment quay… và dành cho các hệ đối xứng trục khác nữa.
Ngôn ngữ toán học của vector và số phức có sự tương hỗ trong các mô hình vật lý. Toán tử tịnh tiến làm nên vector, còn toán tử quay làm nên số phức. Do đó vector tương ứng với chuyển động tịnh tiến, còn số phức tương ứng với chuyển động quay.
Tác giả: Trần Hải Cát
