Gần đây tôi đang cố tạo “phong cách” cho các công bố khoa học của mình bằng cách làm cho nó có tính nghệ thuật. Một trong những “mưu mẹo” của tôi là tôi đã sử dụng tỷ lệ vàng cho các đồ thị trong công bố. Thay vì sử dụng tỷ lệ 1:1 hoặc 3:4 như trước kia, các đồ thị hiện nay được tôi biểu diễn trong tỷ lệ vàng 1:1.618. Có lẽ sẽ có ai đó hỏi tôi là: Tại sao nó lại thẩm mỹ hơn? Thú thực thì tôi cũng không biết, chỉ đơn giản là tôi cảm giác nó đẹp hơn. Không phải ngẫu nhiên tôi cảm giác vậy, đằng sau tỷ lệ vàng là cả một lịch sử và những câu chuyện. Có những nhà khoa học cho rằng chúng ta đã phóng đại tính thẩm mỹ của tỷ lệ vàng một cách mù quáng và sai lầm. Tuy nhiên không thể phủ nhận rằng tỷ lệ vàng xuất hiện ở mọi nơi từ toán học, tự nhiên hay nghệ thuật. Và đây là những câu chuyện về tỷ lệ vàng.
Phương trình bậc hai cổ đại
Một phương pháp xác định tỷ lệ vàng được ghi lại như sau:
“Giả sử bạn có một hình chữ nhật có chiều dài là 1 và chiều rộng bất kỳ là x (với điều kiện x > 1). Sau khi bạn cắt hình chữ nhật đó thành hai phần bao gồm một hình vuông có cạnh là 1 và một hình chữ nhật còn lại có chiều dài là 1 và chiều rộng là x-1 như trong hình 1. Nếu hình chữ nhật mới có tỷ lệ các cạnh bằng với tỷ lệ các cạnh của hình chữ nhật lúc chưa cắt, khi đó giá trị của x tìm được chính là tỷ lệ vàng”
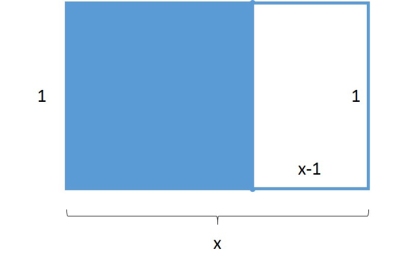
Người Hy Lạp cổ đại đã sử dụng biểu diễn hình học cho bài toán trên, tuy nhiên ngày nay chúng ta sẽ sử dụng đại số như chúng ta được học khi còn nhỏ.
Từ giải thiết của bài toán chúng ta có phương trình sau:
x = 1/(x – 1)
Nhân mỗi vế của phương trình với biểu thức x – 1, ta sẽ thu được phương trình bậc hai như sau:
x2 – x = 1 ⇔ x2 – x – 1 = 0
Ta có nghiệm của phương trình bậc hai trên là:
x = (1 ± √5)/2 ≈ -0.618 hoặc 1.618
Với điều kiện x > 1, cuối cùng ta thu được x = 1.618. Khi đó hình chữ nhật được gọi là có tỷ lệ vàng.
Dãy số Fibonacci
Một vấn đề toán học khác để xác định tỷ lệ vàng đó là sử dụng dãy số Fibonacci. Fibonacci là một dãy số rất nổi tiếng với bài toán con thỏ. Để gợi nhớ lại cho các bạn tôi sẽ nói lại bài toán con thỏ này.
Bắt đầu bằng một cặp thỏ đực và cái vừa được sinh ra, câu hỏi là bao nhiêu cặp thỏ có thể được sinh ra trong một năm bởi một cặp thỏ ban đầu? với các giả định sau đây:
– Thỏ bắt đầu giao phối sau một tháng từ khi sinh ra.
– Thời kỳ mang thai của thỏ cái là một tháng.
– Thỏ cái sẽ sinh ra một thỏ đực và một thỏ cái sau một tháng mang thai.
– Các con thỏ không chết.
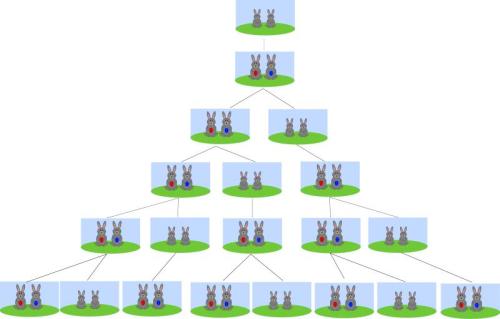
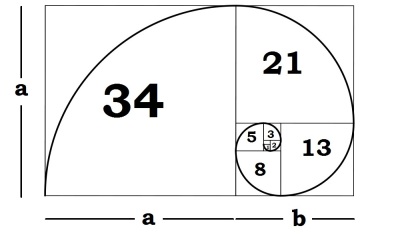
Một sơ đồ biểu diễn được minh hoạ như hình 2. Tháng đầu tiên cặp thỏ vẫn ở độ tuổi trưởng thành và không thể giao phối. Tại tháng thứ hai, các cặp thỏ bắt đầu giao phối nhưng chưa sinh con. Sang tháng thứ ba, cặp thỏ con đầu tiên chào đời, chúng ta có hai cặp thỏ. Sang tháng thứ 4, cặp thỏ thứ nhất tiếp tục sinh thêm một cặp thỏ mới trong khi cặp thỏ thứ hai mới bắt đầu giao phối, chúng ta có ba cặp thỏ lúc này. Điều này cứ tiếp tục như vậy, sau một năm chúng ta sẽ có 233 cặp thỏ. Thật là một tốc độ sinh sản khủng khiếp đúng không các bạn. Vậy cuối cũng dãy số Fibonacci sẽ được biểu diễn như sau 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … Trong đó nguyên tắc là số tiếp theo bằng tổng hai số trước nó.
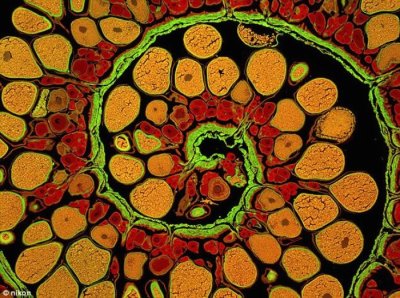
Mặc dù được hiểu đơn giản thông qua bài toán con thỏ, tuy nhiên dãy số Fibonacci xuất hiện rất nhiều trong tự nhiên như loạt hình liệt kê phía dưới.
Trong tự nhiên dãy Fibonacci thường được biểu diễn hình học bởi một chuỗi xoắn ốc như trong hình 3 với các cạnh hình vuông lần lượt là các con số 1, 2, .., 21, 34, .. trong dãy Fibonacci. Khi đó tỷ lệ của hình chữ nhật tổng thể gần bằng với tỷ lệ vàng 1.618.
Hội hoạ
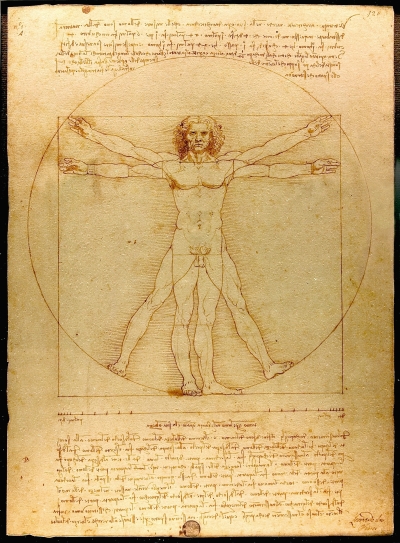
Nếu chỉ dừng ở toán học và vài minh hoạ trong tự nhiên có lẽ vẫn chưa thuyết thục được các bạn về tính thẩm mỹ của tỷ lệ vàng, do đó chúng ta sẽ tiếp tục đi tới nghệ thuật. Xem các nghệ sĩ làm gì với tỷ lệ vàng. Thực tế là hội hoạ cũng là sở thích của tôi từ nhỏ. Do đó tôi đảm bảo với các bạn, bằng cách nào đó tỷ lệ vàng luôn đi vào hội hoạ hoặc điêu khắc như một tỷ lệ hài hoà và cân đối trong bố cục. Ví dụ nổi tiếng nhất được nhắc tới có lẽ là bức tranh “Người Vitruvius” của Leonardo Da Vinci [Hình 4]. Người đàn ông khoả thân trong bức tranh có một tỷ lệ số đo cơ thể được coi là lý tưởng. Tỷ lệ vàng này cũng được sử dụng như chuẩn mực của hội hoạ và điêu khắc thời kì Phục Hưng bởi một loạt các nghệ sĩ như Michelangelo, Raphael, Rembrandt, Seurat, và Salvador Dali.
Giờ đây tôi đang cố gắng sử dụng nó như một tỷ lệ chuẩn mực trong các đồ thị của mình. Tôi thấy điều đó khá thú vị, còn bạn thì sao. Với những người không làm khoa học tôi nghĩ điều này cũng bổ ích, khi lúc nào đó bạn có dịp áp dụng điều này. Hay những bà mẹ kể cho con mình về câu chuyện toán học thú vị thông qua chiếc vỏ ốc hay bông hoa hướng dương hoặc hoa cúc. Có lẽ một ngày nào đó con bạn sẽ trở thành một nhà toán học lớn. Hi vọng các bạn thích thú với câu chuyện trên, tôi sẽ tiếp tục chia sẻ những câu chuyện về những con số thú vị khác về những con số mà ai cũng biết như số PI ở các bài sau.
Tác giả: Nguyễn Tuấn Hùng