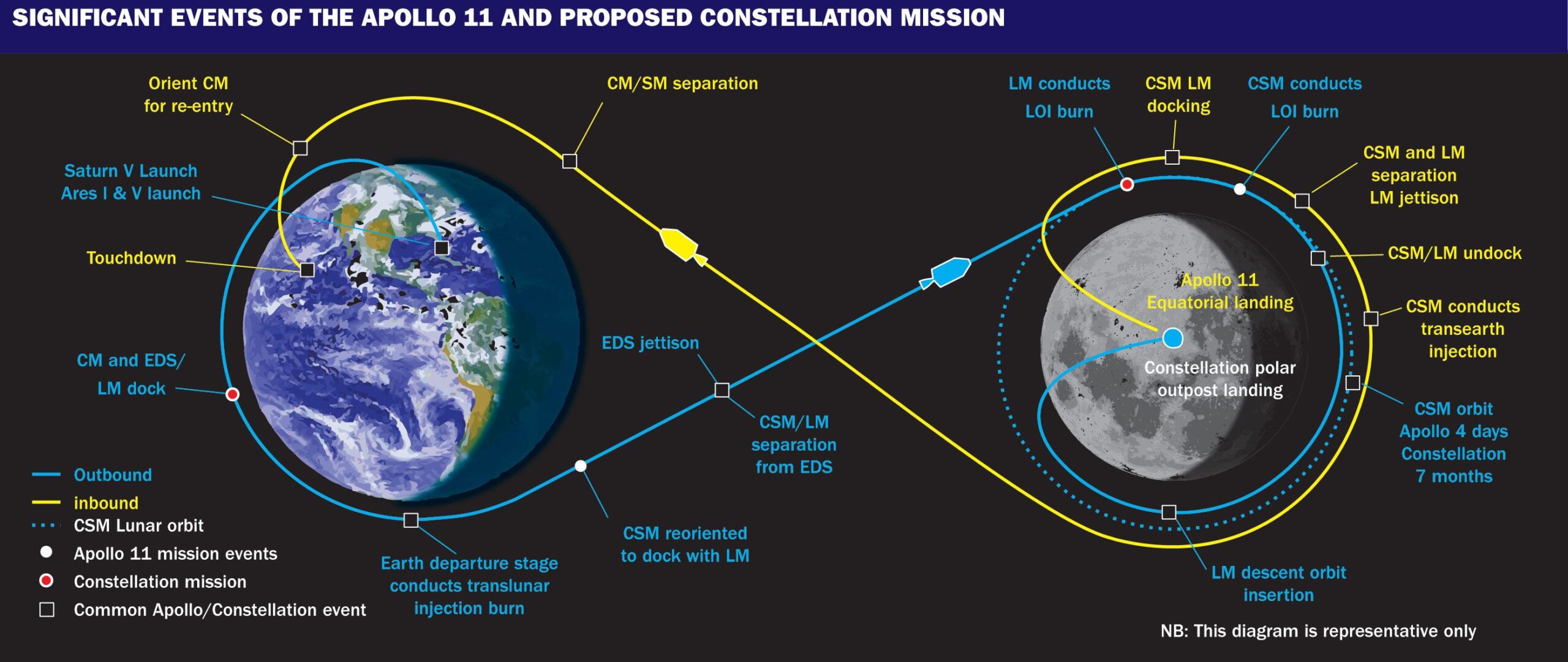
Apollo là chương trình không gian lớn của Hoa Kỳ, hoàn tất sứ mệnh đưa con người lên Mặt trăng lần đầu tiên vào năm 1969. Hành trình của Apollo bao gồm nhiều giai đoạn phức tạp, cần nhiều tính toán để tìm ra đường đi tối ưu, tiết kiệm thời gian và năng lượng. Video sau đây trình bày kết quả mô phỏng phần chính của quỹ đạo tàu Apollo, thực hiện trên Matlab, dựa trên quan điểm chuyển động men theo hố thế.
Di chuyển tự do trong hố thế
Trường lực hấp dẫn Trái đất tạo nên một hố thế hyperbol, với thế năng tỉ lệ nghịch với khoảng cách đến tâm của nó:
\[\varphi=-G\frac{Mm}{r},\]
trong đó \(G\) – hằng số hấp dẫn. Người ta lấy vũ trụ làm gốc thế năng bằng không, cho nên miệng hố thế sẽ tiệm cận với mức không, còn hố thế trũng xuống theo chiều âm. Hình dáng của hố thế miêu tả trên hình 1, kèm theo một vài quỹ đạo của vật được ném đi từ bề mặt Trái đất.
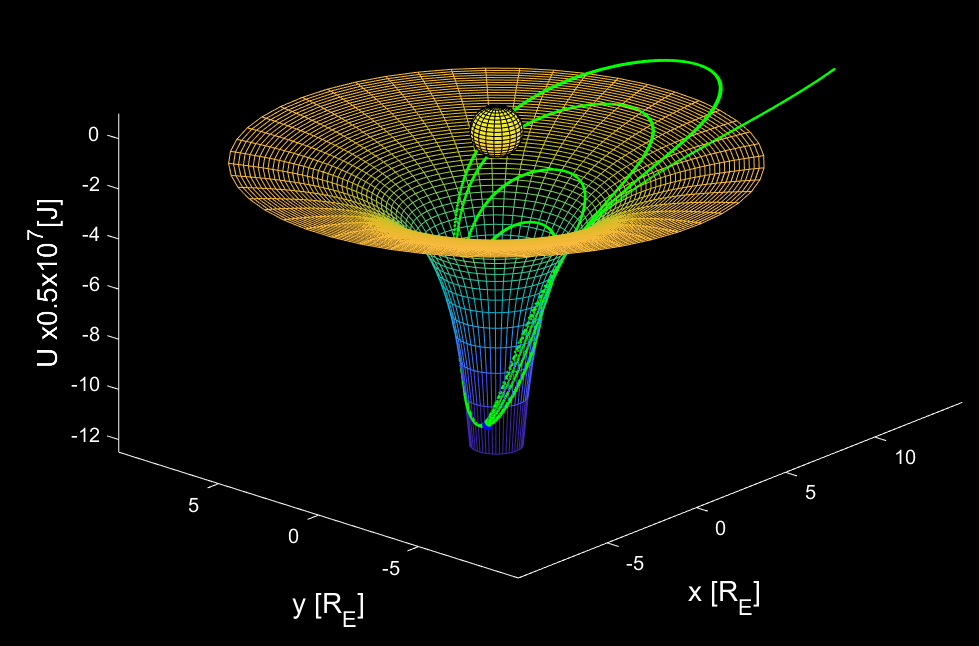
Quỹ đạo nhỏ nhất tương ứng với tốc độ ném \(v_1=\sqrt{gR}=\mathrm{7.9}\) km/s, vật sẽ bay đúng theo đường tròn ôm sát bề mặt Trái đất và không quay trở lại. Ta gọi đó là tốc độ vũ trụ cấp một. Khi bắn ở tốc độ cao hơn, vật sẽ chuyển động theo những đường elip. Do cơ năng bảo toàn, nên khi càng gần Trái đất, vật càng bị kéo xuống đáy hố và chuyển động nhanh hơn. Ngược lại, khi ra xa trên rìa cao, tốc độ vật càng chậm lại. Tốc độ ném ban đầu càng lớn, năng lượng của vật càng cao, elip sẽ càng nở rộng về kích thước. Tính toán chi tiết cho thấy, để vật hoàn toàn thoát ra khỏi hố, nó cần có tốc độ ban đầu ít nhất bằng:
\[v_2=\sqrt{2gR}=\mathrm{11.2\,km/s}.\label{eq:1}\tag{1}\]
Đó chính là tốc độ vũ trụ cấp hai. Thiên thể khối lượng càng lớn sẽ tạo ra hố thế càng sâu, tốc độ thoát ra khỏi hố, hay tốc độ vũ trụ cấp hai sẽ càng lớn.
Tương tự, Mặt trăng cũng tạo quanh nó một hố thế, nhưng cạn hơn. Quả thực, thế gia tốc rơi tự do và bán kính Mặt trăng vào công thức \eqref{eq:1}, sẽ thấy được rằng với tốc độ vũ trụ cấp hai đối với Mặt trăng chỉ vào khoảng \(\mathrm{2.4\,km/s}\).
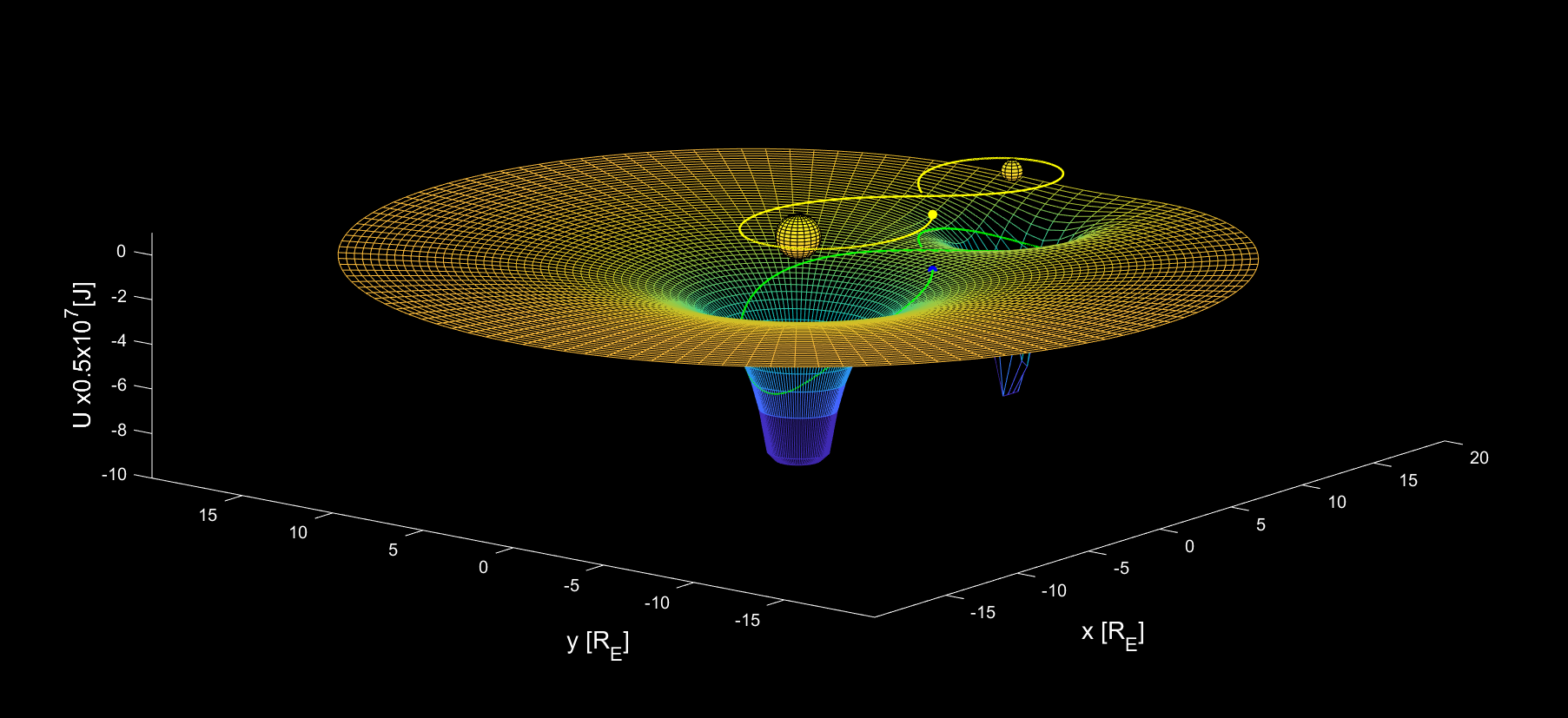
Ta hãy nhắc lại quy tắc du hành lên một thiên thể ngoài Trái đất. Đầu tiên, tàu vũ trụ cần một lực đẩy phản lực từ động cơ tên lửa để leo lên đến miệng hố thế Trái đất. Giữa khoảng không bao la của vũ trụ là nền phẳng bằng không của thế năng, tàu gần như sẽ di chuyển tự do theo quán tính. Sau đó, tàu sẽ định hướng và mon men đi vào hố của thiên thể cần hạ cánh.
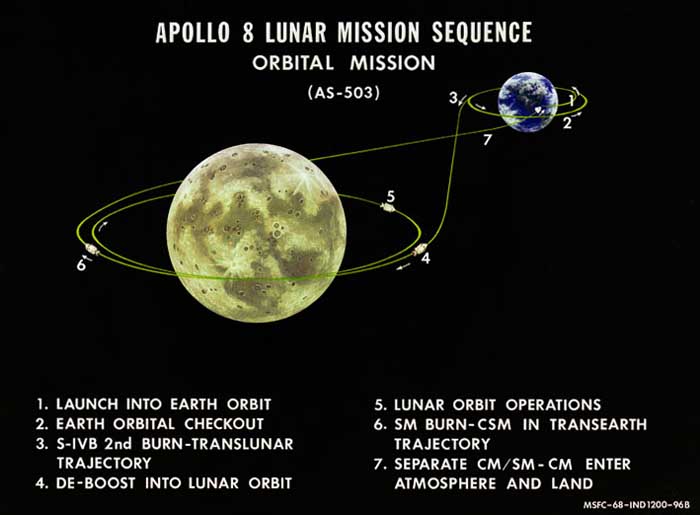
Mặt trăng nằm tương đối gần Trái đất, với khoảng cách \(384\) nghìn kilomet, mất chỉ hơn một giây cho ánh sáng di chuyển. Trái đất và Mặt trăng tạo nên hai hố thế nằm khá gần nhau như miêu tả trên hình 2, giao nhau và hình thành nên một hành lang hẹp, như một thung lũng hơi trũng xuống. Từ đó các nhà khoa học và kĩ sư đã đưa ra ý tưởng hết sức độc đáo, theo đó tàu Apollo được định hướng ban đầu sao cho tàu sẽ tự động men theo thung lũng thế năng để đi vào hố thế Mặt trăng một cách tự nhiên, theo quỹ đạo hình số 8. Việc này giúp cho tàu di chuyển từ quỹ đạo Trái đất sang quỹ đạo Mặt trăng với năng lượng tiêu tốn rất nhỏ, gần như bay tự do dưới trường hấp dẫn của hai thiên thể.
Hành trình Apollo
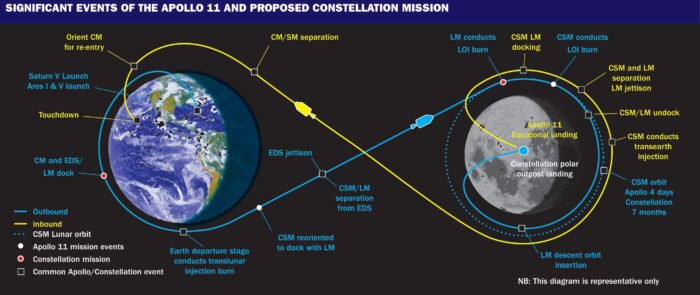
Hành trình của Apollo 11 có thể tóm gọn như sau:
- Tên lửa Saturn V đồ sộ giúp Apollo và ba phi hành gia thoát khỏi miệng hố Trái đất.
- Apollo sau đó men theo hành lang hẹp giữa hai hố theo vòng số 8, đi vào miệng hố Mặt trăng.
- Từ miệng hố Mặt trăng, hai phi hành gia theo modul Mặt trăng tách ra khỏi modul điều khiển, hạ xuống đáy hố.
- Họ đi dạo, chụp ảnh.
- Phi hành gia dùng phần trên của modul Mặt trăng nhỏ gọn, có tên lửa đẩy loại nhỏ, đủ đưa phi hành gia lên miệng hố Mặt trăng, ráp với modul điểu khiển và trở về.
Code chương trình Matlab
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 | function Gravity_Earth_Moon % Author: Tran Hai Cat % Lecturer in Physics, HCM University of Technology and Education % - Dai hoc Su pham Ky thuat Tp. Ho Chi Minh % Created: 2019.03.20 clc; clear variables close all; %% CONSTANTS G = 6.67e-11; % Gravity constant M_earth = 5.97219e24; % Mass of Earth R_earth = 6371e3; % Radius of Earth M_moon = 0.5*M_earth; % Mass of Moon %% INPUT PARAMETRS r = [-2*R_earth 0 0]; % Initial possition v = [0 -6.996e3 0]; % Initial velocity N_orbit = 800; dt = 100; %% Gravitational Potential norm_U = 2e-7; rmin = R_earth; rmax = 20*R_earth; position_moon = [15*R_earth,0,0]; Nr = 55; Nalpha = 120; radius = linspace(rmin,rmax,Nr); alpha = linspace(0,2*pi,Nalpha); [Radius,Alpha] = meshgrid(radius,alpha); X_matrix = Radius.*cos(Alpha); Y_matrix = Radius.*sin(Alpha); Distance_matrix = sqrt(X_matrix.^2+Y_matrix.^2); U_earth_matrix = -G*M_earth./Distance_matrix*norm_U; Distance_matrix = sqrt((X_matrix-position_moon(1)*ones(size(X_matrix))).^2+... (Y_matrix-position_moon(2)*ones(size(Y_matrix))).^2); U_moon_matrix = -G*M_moon./Distance_matrix*norm_U; U_matrix = U_earth_matrix+U_moon_matrix; for j = 1:Nr for i = 1:Nalpha if U_matrix(i,j)<-10 U_matrix(i,j) = -10; end end end d = 5; t = 0; U_earth = -G*M_earth/sqrt(r(1)^2+r(2)^2)*norm_U; U_moon = -G*M_moon/sqrt((r(1)-position_moon(1))^2+... (r(2)-position_moon(2))^2)*norm_U; U = U_earth+U_moon; orbit_array = zeros(3,N_orbit); orbit_array(:,end) = [r(1)/R_earth,r(2)/R_earth,r(3)/R_earth]; potential_track_array = zeros(3,N_orbit); potential_track_array(:,end) = [r(1)/R_earth,r(2)/R_earth,U]; %% FIGURE figure('name','Analys koefficients of Fourier series',... 'color','black','numbertitle','off') set(gca,'color','k','xcolor','w','ycolor','w','zcolor','w') hold on mesh(X_matrix/R_earth,Y_matrix/R_earth,U_matrix); view(-60,20); axis equal rotate3d on xlabel('x [R_E]','fontsize',14); ylabel('y [R_E]','fontsize',14); zlabel('U x0.5x10^7[J]','fontsize',14); % Draw Earth sphere; % Draw Moon [x,y,z] = sphere(10); x = x*0.5; y = y*0.5; z = z*0.5; surf(x+position_moon(1)/R_earth,y+position_moon(2)/R_earth,z+position_moon(3)/R_earth); hf_sputnik = plot3(r(1)/R_earth,r(2)/R_earth,r(3)/R_earth,... 'yo','markersize',d,'markerfacecolor','y'); hf_orbit = plot3(orbit_array(1,:),orbit_array(2,:),orbit_array(3,:),... 'yo','markersize',1); hf_U = plot3(r(1)/R_earth,r(2)/R_earth,U,... 'bo','markersize',d,'markerfacecolor','b'); hf_potential_track = plot3(potential_track_array(1,:),... potential_track_array(2,:),potential_track_array(3,:),... 'go','markersize',1); %% ANIMATION while 1 t = t+dt; dis_to_earth = sqrt(r(1)^2+r(2)^2); dis_to_moon = sqrt((r(1)-position_moon(1))^2+(r(2)-position_moon(2))^2); a_earth = -G*M_earth/dis_to_earth^3*r; a_moon = -G*M_moon/dis_to_moon^3*(r-position_moon); a = a_earth+a_moon; v = v+a*dt; r = r+v*dt+0.5*a*dt; U_earth = -G*M_earth/sqrt(r(1)^2+r(2)^2)*norm_U; U_moon = -G*M_moon/sqrt((r(1)-position_moon(1))^2+... (r(2)-position_moon(2))^2)*norm_U; U = U_earth+U_moon; orbit_array(:,1:end-1) = orbit_array(:,2:end); orbit_array(:,end) = r./R_earth; potential_track_array(:,1:end-1) = potential_track_array(:,2:end); potential_track_array(:,end) = [r(1)/R_earth,r(2)/R_earth,U]; set(hf_sputnik,... 'xdata',r(1)/R_earth,... 'ydata',r(2)/R_earth,... 'zdata',r(3)/R_earth); set(hf_orbit,... 'xdata',orbit_array(1,:),... 'ydata',orbit_array(2,:),... 'zdata',orbit_array(3,:)); set(hf_U,'xdata',r(1)/R_earth,'ydata',r(2)/R_earth,'zdata',U); set(hf_potential_track,... 'xdata',potential_track_array(1,:),... 'ydata',potential_track_array(2,:),... 'zdata',potential_track_array(3,:)); pause(0.01); end |